モノイド圏：評価写像の双関手性 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「準マルコフ圏からなる2-圏」という記事を書いてからもうすぐ3週間です。「準マルコフ圏からなる2-圏」に引き続く記事で、「“準マルコフ圏からなる2-圏”内の余モナドの余クライスリ圏が準マルコフ圏になる」ことを示す予定だったのですが、引き続く記事は既に10本以上。こんなに長くなるとは思わなんだ。細部まで詰めようと思うと、けっこうな手間ですね。「ちょっとサボろうかな」という気分になっています(苦笑)。

今回述べる評価写像の双関手性は、後の計算でどうしても必要なのですが、ある程度は直感に頼った説明／端折った説明をする（サボる）ことにします。 $\newcommand{\In}{\text{ in } } \newcommand{\hyp}{\text{-} } \newcommand{\id}{\mathrm{id}} \newcommand{\Ev}{\mathrm{Ev}} \newcommand{\ev}{\mathrm{ev}} \newcommand{\moveTo}{\rightsquigarrow } \newcommand{\Iff}{\Leftrightarrow } \newcommand{\cat}[1]{ \mathcal{#1} } \newcommand{\u}[1]{ \underline{#1} } \newcommand{\I}{\mathrm{I}} \newcommand{\A}{\wedge } % \newcommand{\Mor}{\mathrm{Mor} } \newcommand{\EvL}{ (\!| } \newcommand{\EvR}{ |\!) } % \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Declare}{\Keyword{Declare } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Where}{\Keyword{Where } }% \newcommand{\Holds}{\Keyword{Holds } }%$

内容：

ここで扱う圏
評価写像の宣言
BUNツリーへの圏の対象の代入
閉じたBUNツリーの評価
マックレーン変形の評価
評価写像の双関手性
評価写像のエレベーター法則
まとめ

ここで扱う圏

「豊饒化〈豊穣化〉ドクトリン」で説明したネーミングルールに従い、豊饒化〈豊穣化〉された圏やオペラッドはハイフンが入った名前で呼びます。例えば、「亜群-オペラッド」のように。

亜群-オペラッド ${\bf BUNTree}$ の複ホム亜群〈multihom-groupoid〉を

$\quad {\bf BUNTree}(n) = {\bf BUNTree}(n, 1)$

とします。定義より、複ホム亜群は亜群（特殊な圏）なので、その対象集合とホムセット達を持ちます。

対象集合 $|{\bf BUNTree}(n)|$ は、幅が $n$ のBUNツリー（の伸縮同値類）の集合
ツリー $s, t\in |{\bf BUNTree}(n)|$ に対するホムセット ${\bf BUNTree}(n)(t, s)$ は、ツリー $s$ をツリー $t$ へと変形するマックレーン変形の集合

つまり：

$\quad \beta \in {\bf BUNTree}(n)(s, t) \\ \Iff \beta : s \to t \In {\bf BUNTree}(n)\\ \Iff \beta :: s \moveTo t : n \to 1 \In {\bf BUNTree}$

マックレーン変形のプロファイルは引き続き波矢印で書きますが、2-射（2次元の構成素）であることを強調するためにコロンは2個付けることにします。

[補足]「余計な話？厳密2-亜群オペラッドとモノイド圏」では、 ${\bf BUNTree}$ に3次元の射（マックレーン多角形）も含めた厳密2-亜群-オペラッド（この呼び名については「豊饒化〈豊穣化〉ドクトリン」参照）だとしました。が、この記事では3次元の射は考えずに亜群-オペラッドと考えます。[/補足]

$\cat{C}$ は（小さい）モノイド圏で、 $\u{\cat{C}}$ をその台圏〈underlying category〉とします。 $\cat{I}$ は自明なモノイド圏で、 $\u{\cat{I}}$ は自明圏とします。 $\u{\cat{C}^n} = \u{\cat{C}}^n$ は、直積の意味での圏の累乗ですが、特別な場合として：

$\u{\cat{C}}^0 = \u{\cat{I}}$
$\u{\cat{C}}^1 = \u{\cat{C}}$

“亜群-オペラッド ${\bf BUNTree}$ の複ホム亜群”と“モノイド圏 $\mathcal{C}$ の台圏 $\underline{\mathcal{C}}$ の累乗”はどちらも（小さい）圏なので、任意の自然数 $n$ に対して次が成立します。

$\quad {\bf BUNTree}(n) \in |{\bf Cat}|\\ \quad \u{\cat{C}}^n \in |{\bf Cat}|$

2つの圏の直積も圏になるので：

$\quad {\bf BUNTree}(n)\times \u{\cat{C}}^n \in |{\bf Cat}|$

評価写像の宣言

これから、 $\Ev_n^\cat{C}: {\bf BUNTree}(n)\times \u{\cat{C}}^n \to \u{\cat{C}}$ という双関手〈二項関手〉を定義したいのですが、当面は双関手かどうかは分からないので単に写像と呼んでおきます。 $\Ev_n^\cat{C}$ は、モノイド圏 $\cat{C}$ と自然数 $n$ に対して決まるのですが、上下の添字は鬱陶しいので、

$\quad \Ev = \Ev^\cat{C} = \Ev_n^\cat{C}$

のように省略します。 $\Ev$ は "evluation" からで、評価写像〈evaluation map〉と呼びます。

写像 $\Ev$ は、次の2つの写像に対してオーバーロードされた名前です。

$\quad \Ev: |{\bf BUNTree}(n)|\times |\u{\cat{C}}^n| \to |\u{\cat{C}}| \\ \quad \Ev: \Mor({\bf BUNTree}(n)) \times \Mor(\u{\cat{C}}^n) \to \Mor(\u{\cat{C}})$

これから定義すべきものを先に宣言しておくと次のようになります。

$\For t \in |{\bf BUNTree}(n)|\\ \For \vec{A} \in |\u{\cat{C}}^n| = |\u{\cat{C}}|^n\\ \Declare \Ev(t, \vec{A}) \in |\u{\cat{C}}|\\ \:\\ \For \beta \in {\bf BUNTree}(n)(t, t')\\ \For \vec{f} \in \u{\cat{C}}^n(\vec{A}, \vec{B})\\ \Declare \Ev(\beta, \vec{f}) \in \u{\cat{C}}(\Ev(t, \vec{A}), \Ev(t', \vec{B}) )$

圏 $\u{\cat{C}}^n$ の対象と射には矢印を乗せています。

$\quad \vec{A} = (A_1, \cdots, A_n) \in |\u{\cat{C}}|^n\\ \quad \vec{B} = (B_1, \cdots, B_n) \in |\u{\cat{C}}|^n\\ \quad \vec{f} = (f_1, \cdots, f_n) \in \u{\cat{C}}^n(\vec{A}, \vec{B})$

BUNツリーへの圏の対象の代入

この節は評価写像の定義のための準備です。

「反ラックス・モノイド関手の一般余結合律 // 二分木の半オペラッド構造」でツリーに対する置換〈代入〉演算を導入して、「BUNツリーの亜群オペラッド構造 // オペラッド＝複圏」で記法を整理しました。BUNツリーに対して次の記法を定義しました。

$t[s/i]$
$t[s_1, \cdots, s_n] = t[s_1/1, \cdots, s_n]$

今まで、プレースホルダーに対して代入できるのはBUNツリーでしたが、圏 $\cat{D}$ （ $\cat{D}$ は任意）の対象も代入できるとします。それを次のように書きます。

$t[A/i] \;\text{ for }A \in |\cat{D}|$
$t[A_1, \cdots, A_n] = t[A_1/1, \cdots, A_n] \;\text{ for }A_i \in |\cat{D}|$

注意すべきは、この時点で得られるのは“リーフが圏の対象であるBUNツリー”であって、圏の対象ではないことです。

今出した（対象が代入された）BUNツリー

$\quad t[A/1, B/3] = ( (-\A-)\A -)[A/1, B/3] = ( (A\A-)\A B)$

は、プレースホルダー ' $-$ ' が残ってますが、プレースホルダーがすべて圏 $\cat{D}$ の対象に置換されているツリーを考えます。プレースホルダーが残っていないBUNツリーを閉じたBUNツリー〈closed BUN tree〉と呼ぶことにします*1。閉じたBUNツリーは、適当な自然数 $n$ に対して次の形に書けます。

$\quad t[\vec{A}] \;\text{ for }t \in |{\bf BUNTree}(n)|, \vec{A} \in |\cat{D}|^n$

したがって、

$\quad (\text{幅} n \text{の閉じたBUNツリーの集合}) \cong |{\bf BUNTree}(n)| \times |\cat{D}|^n$

以下、閉じたBUNツリーの集合と $|{\bf BUNTree}(n)| \times |\cat{D}|^n \;\text{ for }n \in {\bf N}$ を適宜同一視します。

閉じたBUNツリーの評価

$\cat{C}$ をモノイド圏として、 $\cat{D} = \u{\cat{C}}$ の場合を考えます。この場合は、閉じたBUNツリー $t[\vec{A}] \in {\bf BUNTree}(n) \times |\u{\cat{C}}|^n$ を、 $\cat{C}$ のモノイド積 $\otimes = \otimes^\cat{C}$ を使って評価（実際に計算）することができます。実際に計算した値を、

$\quad \ev(t[\vec{A}]) \in |\u{\cat{C}}|$

とします。 $\ev = \ev^\cat{C}$ はモノイド積を実際に計算する写像です。

評価写像（の一部）は次の定義で与えられます。

$\For t \in |{\bf BUNTree}(n)|\\ \For \vec{A} \in |\u{\cat{C}}^n| = |\u{\cat{C}}|^n\\ \Define \Ev(t, \vec{A}) := \ev(t[\vec{A}]) \in |\u{\cat{C}}|$

「反ラックス・モノイド関手の一般余結合律 // 二分木とモノイド圏」では、今定義した $\Ev(t, \vec{A})$ を $t(\vec{A})$ と書いています。丸括弧記号は他の用途でも使われるので混乱のリスクがありますね。丸括弧を凸レンズ括弧に変更します。

$\quad t\EvL \vec{A} \EvR := \Ev(t, \vec{A}) = \ev(t[\vec{A}])$

$\ev$ や $\Ev$ が定義できるのは $\cat{C}$ がモノイド積を持つからです。単なる圏に対して評価写像が定義できるわけではありません。

なお、 $(t, \vec{A})$ と $t[\vec{A}]$ を完全に同一視するなら、 $\Ev$ と $\ev$ を区別する意味はないのですが、気分的には違う（あるいは、定式化を変えれば違う）ので、 $\Ev$ と $\ev$ を使い分けます。 $\ev$ は閉じたBUNツリー専用で、 $\Ev$ は一般的な評価写像です。

マックレーン変形の評価

$\beta$ をマックレーン変形だとすると、次のように書けます。

$\quad \beta:: t \moveTo t' = t^\beta \In {\bf BUNTree}\\ \Iff \beta: t \to t' = t^\beta \In {\bf BUNTree}(n)\\ \Where n = \mathrm{width}(t)$

一方、 $\u{\cat{C}}^n$ の射 $\vec{f}$ は次のように書けます。

$\quad \vec{f}:\vec{A} \to \vec{B} \In \u{\cat{C}}^n\\ \Where\\ \quad \vec{A} = (A_1, \cdots, A_n),\, \vec{B} = (B_1, \cdots, B_n)\\ \quad \vec{f} = (f_1, \cdots, f_n)\\ \quad f_i : A_i \to B_i \In \u{\cat{C}} \;\text{ for }i = 1, \cdots, n$

これから、 $\Ev(\beta, \vec{f})$ を定義したいのですが、次のことは分かっているとしていいでしょう。

$\Ev(t, \vec{A}), \Ev(t, \vec{B}), \Ev(t', \vec{A}), \Ev(t', \vec{B}) \in |\u{\cat{C}}|$ ： BUNツリーに $\u{\cat{C}}$ の対象を代入した（プレースホルダーを対象で置換した）ツリーを、 $\cat{C}$ のモノイド積で評価した対象。
$\Ev(t, \vec{f}):\Ev(t, \vec{A}) \to \Ev(t, \vec{B}),\;\Ev(t', \vec{f}):\Ev(t', \vec{A}) \to \Ev(t', \vec{B}) \In \u{\cat{C}}$ ：射のツリー状の組み合わせを、 $\cat{C}$ の“射に対するモノイド積”で評価した射。
$\Ev(\beta, \vec{A}),\, \Ev(\beta, \vec{B}) \In \u{\cat{C}}$ ：モノイド圏の定義から導かれる、マックレーン変形に対する $\cat{C}$ の構造同型射。

具体例を、次のセッティングで考えてみましょう。

$t = ( (-\A-)\A-) \in |{\bf BUNTree}(3)|$
$t' = ( - \A(-\A-) )\in |{\bf BUNTree}(3)|$
$\beta = \mathrm{LSw} \in {\bf BUNTree}(3)(t, t')$
$\vec{A} = (A, B, C) \in |\u{\cat{C}}|^3$
$\vec{B} = (X, Y, Z) \in |\u{\cat{C}}|^3$
$\vec{f} = (f, g, h): (A, B, C) \to (X, Y, Z) \In \u{\cat{C}}^3$

これらに対する $\Ev(\hyp, \hyp)$ は次のようになります。

$\Ev(t, \vec{A}) = \Ev( ( (-\A-)\A-), (A, B, C) ) = (A\otimes B)\otimes C \in |\u{\cat{C}}|$
$\Ev(t, \vec{B}) = \Ev( ( (-\A-)\A-), (X, Y, Z) ) = (X\otimes Y)\otimes Z \in |\u{\cat{C}}|$
$\Ev(t', \vec{A})= \Ev( ( - \A(-\A-) ), (A, B, C) ) = A\otimes (B\otimes C) \in |\u{\cat{C}}|$
$\Ev(t', \vec{B}) = \Ev( ( - \A(-\A-) ), (X, Y, Z) ) = X\otimes (Y\otimes Z) \in |\u{\cat{C}}|$
$\Ev(t, \vec{f}) = \Ev( ( (-\A-)\A-), (f, g, h) ) = (f\otimes g)\otimes h :(A\otimes B)\otimes C \to (X\otimes Y)\otimes Z \In \u{\cat{C}}$
$\Ev(t', \vec{f}) = \Ev( ( - \A(-\A-) ), (f, g, h) ) = f\otimes (g\otimes h) :A\otimes( B\otimes C) \to X\otimes (Y\otimes Z) \In \u{\cat{C}}$
$\Ev(\beta, \vec{A}) = \Ev(\mathrm{LSw}, (A, B, C)) = \alpha_{A, B, C}:(A\otimes B)\otimes C \to A\otimes (B\otimes C) \In \u{\cat{C}}$
$\Ev(\beta, \vec{B}) = \Ev(\mathrm{LSw}, (X, Y, Z) ) = \alpha_{X, Y, Z}:(X\otimes Y)\otimes Z \to Z\otimes (Y\otimes Z) \In \u{\cat{C}}$

$\Ev(\hyp, \hyp)$ の2変数の片側を特定の対象に固定したとき、残りの変数に関して関手になります。

関手性1： $\Ev(\hyp, \vec{A}): {\bf BUNTree}(n) \to \u{\cat{C}}$ は関手
関手性2： $\Ev(t, \hyp): \u{\cat{C}}^n \to \u{\cat{C}}$ は関手

この事実の証明はサボります。直感的には明らかだと思います（たぶん）。

さて、肝心の $\Ev(\beta, \vec{f})$ ですが、それは次のように定義します。

$\For \beta:t \to t' \In {\bf BUNTree}(n)\\ \For \vec{f}:\vec{A} \to \vec{B} \In \u{\cat{C}}^n\\ \Define \Ev(\beta, \vec{f}) := \Ev(\beta, A); \Ev(t', \vec{f})$

この定義がうまく働くためには、次の等式が成立している必要があります。

$\For \beta:t \to t' \In {\bf BUNTree}(n)\\ \For \vec{f}:\vec{A} \to \vec{B} \In \u{\cat{C}}^n\\ \Holds \Ev(\beta, \vec{A}); \Ev(t', \vec{f}) = \Ev(t, \vec{f}); \Ev(\beta, \vec{B})$

要求されている等式は、 $\Ev$ の“エレベーター法則”です。

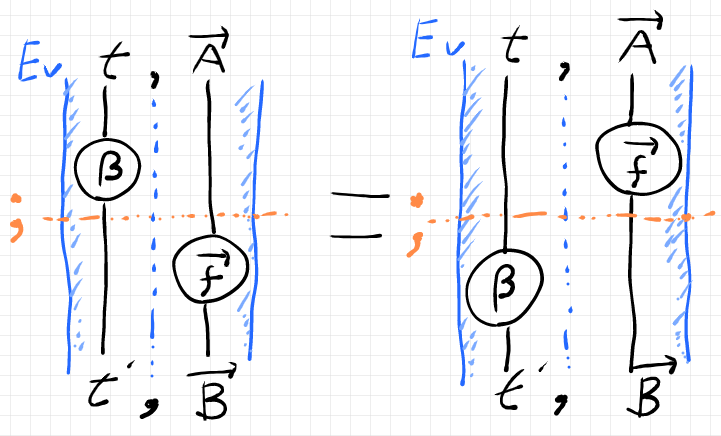
先の例の場合なら、エレベーター法則は次のようになります。

$\For \mathrm{LSw}:( (-\A -)\A -) \to (- \A(-\A -) ) \In {\bf BUNTree}(n)\\ \For (f, g, h):(A, B, C) \to (X, Y, Z) \In \u{\cat{C}}^n\\ \Holds \alpha_{A, B, C}; \big(f\otimes (g \otimes h)\big) = \big( (f \otimes g)\otimes h \big); \alpha_{X, Y, Z}$

評価写像の双関手性

前節のエレベーター法則がもし成立しているなら（今は成立しているかどうかわかってないが）、 $\Ev$ が双関手〈二項関手〉であることが言えます。双関手性は次の等式で表せるのでした。

$\Ev(\beta; \gamma, \vec{f}; \vec{g}) = \Ev(\beta, \vec{f}) ; \Ev(\gamma, \vec{g})$
$\Ev(\id_t, \id_\vec{A}) = \id_{\Ev(t,\vec{A})}$

2番目は明らかでしょうから、1番目（交替律）を示しましょう。次の仮定をします。

$\quad \vec{f} : \vec{A} \to \vec{B} \In \u{\cat{C}}^n\\ \quad \vec{g} : \vec{B} \to \vec{C} \In \u{\cat{C}}^n\\ \quad \beta : t \to t' \In {\bf BUNTree}(n)\\ \quad \gamma: t' \to t'' \In {\bf BUNTree}(n)$

次のように計算します。

$\quad \Ev(\beta; \gamma, \vec{f}; \vec{g}) \\ \qquad \text{定義}\\ = \Ev(\beta; \gamma, \vec{A}); \Ev(t'', \vec{f};\vec{g})\\ \qquad \text{関手性1, 関手性2}\\ = \big( \Ev(\beta, \vec{A}) ;\Ev(\gamma, \vec{A}) \big); \big( \Ev(t'', \vec{f});\Ev(t'', \vec{g}) \big)\\ \qquad \text{結合の結合性}\\ = \Ev(\beta, \vec{A}) ; \big(\Ev(\gamma, \vec{A}) ; \Ev(t'', \vec{f}) \big);\Ev(t'', \vec{g}) \\ \qquad \text{エレベーター法則}\\ = \Ev(\beta, \vec{A}) ; \big(\Ev(t', \vec{f}) ; \Ev(\gamma, \vec{B}) \big);\Ev(t'', \vec{g}) \\ \qquad \text{結合の結合性}\\ = \big( \Ev(\beta, \vec{A}) ; \Ev(t', \vec{f})\big) ; \big( \Ev(\gamma, \vec{B}) \big);\Ev(t'', \vec{g}) \big) \\ \qquad \text{定義}\\ = \Ev(\beta, \vec{f}) ; \Ev(\gamma, \vec{g})$

また、エレベーター法則が成立しているなら $\Ev(\beta, \vec{f})$ の次の2つの定義は一致します。

定義1： $\Ev(\beta, \vec{f}) := \Ev(\beta, \vec{A}); \Ev(t', \vec{f})$
定義2： $\Ev(\beta, \vec{f}) := \Ev(t, \vec{f}); \Ev(\beta, \vec{B})$

評価写像のエレベーター法則

以上で、評価写像がエレベーター法則を満たせば双関手性が出ることは分かりました。エレベーター法則の証明は、BUNツリーの帰納的構成に沿った構造帰納法ということになるでしょう。ここの組み合わせ的議論が面倒で「ちょっとサボろうかな」という気分になったわけです。

帰納法のベースの部分だけは書いておきます。マックレーン変形を構成する基本部品は $\mathrm{LSw}, \mathrm{LDel}, \mathrm{RDel}$ の3つのマックレーン基本変形でした。まず、これらに対してエレベーター法則を確認します。次の等式達です。

$\alpha_{A, B, C}; \big(f\otimes (g \otimes h)\big) = \big( (f \otimes g)\otimes h \big); \alpha_{X, Y, Z}$
$\lambda_{A} ; f = (\id_\I \otimes f) ; \lambda_{X}$
$\rho_{A} ; f = (f\otimes \id_\I) ; \rho_{X}$

これらは $\alpha, \lambda, \rho$ の自然性なのでモノイド圏の定義から成立します。

マックレーン変形は、3つのマックレーン基本変形から順番に組み立てられるので、その組み立て方を $\u{\cat{C}}$ で実行して同型射が得られます。組み立てる前の素材においてエレベーター法則が成立しているなら、組み立てた後でもエレベーター法則が成立していること（帰納法のステップ）が示せれば、すべてのマックレーン変形でエレベーター法則が成立していると言えます。