黒魔術っぷりに驚いた！古典テンソル計算での置換と対称化／反対称化

10年前に、ツビタノビッチ〈Predrag Cvitanovic〉のバードトラックを話題にしたことがあります。

バードトラック -- 群論的なファインマン図

ツビタノビッチ本は、そのときにチラリと眺めただけで、その後見返すことはありませんでした。が、たまたまバードトラック・サイト（http://birdtracks.eu/）が参照されているのをたどって、ツビタノビッチ本（サイトにあるwebbookのリンクから読めます）の目次から第6章に飛んでみたのですが、ビックリしました。

第6章は、置換〈permutation〉や対称化〈symmetrization〉／反対称化〈anti-symmetrization〉の話題です。ツビタノビッチが明示的に説明しているわけではないのですが、古典テンソル計算で置換／対称化／反対称化をどう取り扱うかが推測できます。僕が驚いたのは古典的方法に対して*1で、「ゲゲゲッ、こんなことやっていたのぉー!?」と愕然。

古典的／伝統的なテンソル計算を、僕は“因習的テンソル計算”と呼んだりしてますが、置換／対称化／反対称化の扱いはまさに因習的。これはワケワカランと思うぞ。

ツビタノビッチ本はキッカケになっただけなので、この記事はツビタノビッチ本第6章を解説するものではありません。因習的テンソル計算における置換の“分かりにくい書き表し方”を紹介するものです。対称化と反対称化の話題（これも驚く）はまたいずれ。

内容：

置換の書き表し方
対称群のテンソルベキ表現
デルタ記号による置換の書き表し方
なぜ、こんな書き表し方が採用されたのか

置換の書き表し方

集合 {1, 2, ..., n} からそれ自身への写像 f:{1, 2, ..., n}→{1, 2, ..., n} で全単射〈双射〉であるものをn次の置換〈permutation of degree n〉と呼びます*2。n次の置換の全体は、写像の結合〈合成〉に関して群になるので、この群をn次の置換群〈permutation group of degree n〉と呼びます。置換群を対称群〈symmetric group〉とも呼びます。「置換群」と「対称群」を区別する人もいます*3が、ここでは同義語です。n次の対称群を Sym(n) と書きます。

Sym(n) の要素（つまり、n次の置換）の書き表し方は色々ありますが、例えば Sym(3) の要素を次のように書けば分かりやすいでしょう。

$\begin{bmatrix} 1 & \to & 2 \\ 2 & \to & 3 \\ 3 & \to & 1 \\ \end{bmatrix}$

後の記法との兼ね合いで、次のようにも書きます（矢印は下から上）。

$\newcommand{\uto}{\uparrow}% \begin{bmatrix} 2 & 3 & 1 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix}$

この書き方は場所をとります。行列の2行・3行はいつも同じなので、省略してもいいとします。

$\newcommand{\uto}{\uparrow}% \begin{bmatrix} 2 & 3 & 1 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & 3 & 1 \\ \end{bmatrix}$

簡略化した書き方で、Sym(3) の要素を列挙してみると。

[1 2 3]
[1 3 2]
[2 1 3]
[2 3 1]
[3 1 2]
[3 2 1]

対称群のテンソルベキ表現

ベクトル空間は、実数係数の有限次元ベクトル空間だけを考えます。いくつかのベクトル空間のテンソル積として書かれたベクトル空間をテンソル積ベクトル空間〈tensor product vector space〉と呼びます。より短くテンソル積空間〈tensor product space〉でもいいとします（「テンソル空間」は曖昧語なので使いません）。

ベクトル空間Vに対して、V $\otimes$ V $\otimes$ ... $\otimes$ V と、同じベクトル空間のテンソル積として書かれたベクトル空間をテンソルベキ空間〈tensor power spece〉と呼びましょう。Vのn乗のテンソルベキ空間を V^⊗n と書きます*4。

ベクトル空間Wの線形自己同型写像〈linear automorphism〉の全体を Aut(W) と書きます*5。Aut(W) は線形写像の結合〈合成〉により群となります。n次の対称群〈置換群〉Sym(n) から Aut(V^⊗n) への、標準的な群準同型写像があります。それを、T:Sym(n)→Aut(V^⊗n) とします。

σ∈Sym(n) に対して、σ $\mapsto$ T_σ, T_σ:V^⊗n→V^⊗n
v₁⊗...⊗v_n∈V^⊗n に対して、T_σ(v₁⊗...⊗v_n) := v_σ(1)⊗...⊗v_σ(n)

群の準同型写像 T は、ベクトル空間Vと自然数nにも依存するので、それを明示したいときは、^VTⁿ:Sym(n)→Aut(V^⊗n) と書きます。が、たいていは V, n を省略します（文脈から分かるので）。Tは、群の線形表現の一種なので、対称群の（Vによる）テンソルベキ表現〈tensor power representation〉ともいいます。

n = 3 のときの具体例を出すなら：

T_{[2 3 1]}(v₁⊗v₂⊗v₃) = v₂⊗v₃⊗v₁
T_{[2 1 3]}(v₁⊗v₂⊗v₃) = v₂⊗v₁⊗v₃
T_{[1 3 2]}(v₁⊗v₂⊗v₃) = v₁⊗v₃⊗v₂

これらは、下から上に向かうストリング図で描けば分かりやすいです。

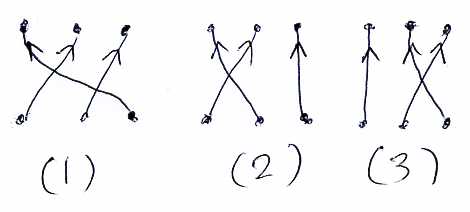
なぜ下から上かと言うと、古典テンソル計算の記法に合わせるためです。

デルタ記号による置換の書き表し方

σ∈Sym(n) に対して、T_σ∈Aut(V^⊗n) を、記号の乱用によりσと同一視することがあります。

T_σ = σ （乱用）

σ, τ∈Sym(n) のときは、σ + τ とか 2σ とかは無意味ですが、σ, τ∈Aut(V^⊗n) とみなせば、σ + τ, 2σ∈End(V^⊗n) として意味があります。ここで、End(V^⊗n) は、必ずしも同型とは限らない線形写像 V^⊗n→V^⊗n の全体です。つまり、記号の乱用の結果、Sym(n) ⊆ Aut(V^⊗n) ⊆ End(V^⊗n) となり、置換に対する足し算やスカラー倍などの線形演算が自由に行なえます。便利ですが、記号の乱用をしていることを明示しないと混乱するでしょう。

さて、古典テンソル計算における T_σ の書き方ですが、ひとつの案としては、上記の記号の乱用により、T_{[2 3 1]} なら [2 3 1] と書く方法があります。しかし、実際には別な方法が取られています。

n = 3 の場合で説明します。まず、添字のセットを2セット用意します。例えば、{i, j, k} と {α, β, γ} 。2セットの添字セットと、番号の集合 {1, 2, 3} を対応付けます。例えば下の表のように。

番号	1	2	3
添字セット 1	i	j	k
添字セット 2	α	β	γ

つまり、次のルールを（通常は暗黙に）仮定します。

文字iと文字αは、番号1を表す。
文字jと文字βは、番号2を表す。
文字kと文字γは、番号3を表す。

番号そのものの代わりに文字を使って置換を表します。例えば：

$\begin{bmatrix} 2 & 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 3 & 1 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix} = \begin{bmatrix} j & k & i \\ \uto & \uto & \uto \\ \alpha & \beta & \gamma \\ \end{bmatrix} \\ \:\\ % \begin{bmatrix} 2 & 1 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & 1 & 3 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix} = \begin{bmatrix} j & i & k \\ \uto & \uto & \uto \\ \alpha & \beta & \gamma \\ \end{bmatrix} \\ \:\\ % \begin{bmatrix} 1 & 3 & 2 \\ \end{bmatrix} = \begin{bmatrix} 1 & 3 & 2 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix} = \begin{bmatrix} \alpha & \gamma & \beta \\ \uto & \uto & \uto \\ i & j & k \\ \end{bmatrix} \\$

2セットの添字セットを上に使うか下に使うかは自由です。ただし、同じ添字セットの文字が上下に混ざるのはダメです。上の例では、下の段（行列の第3行）は順番に並べてますが、シャフルしてもかまいません。

$\begin{bmatrix} 2 & 3 & 1 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \\ \end{bmatrix} = \begin{bmatrix} j & k & i \\ \uto & \uto & \uto \\ \alpha & \beta & \gamma \\ \end{bmatrix} = \begin{bmatrix} k & j & i \\ \uto & \uto & \uto \\ \beta & \alpha & \gamma \\ \end{bmatrix}$

以上のように、2セットの添字セットを上下に配置した形で置換（のテンソルベキ表現）を表します。表し方のバリエーションがものすごくありますが、ともかくも置換を表わせます。さらに、文字'δ'に上下添字を並べた形で置換（のテンソルベキ表現）を書き表します。例を挙げると：

$\:\:\: T_{\begin{bmatrix} 2 & 3 & 1 \end{bmatrix}} = T_{\begin{bmatrix} 2 & 3 & 1 \\ \uto & \uto & \uto \\ 1 & 2 & 3 \end{bmatrix}} \\ = T_{\begin{bmatrix} j & k & i \\ \uto & \uto & \uto \\ \alpha & \beta & \gamma \end{bmatrix}} \\ = \delta^j_\alpha \delta^k_\beta \delta^i_\gamma \\ = \delta^k_\beta \delta^j_\alpha \delta^i_\gamma$

結局、置換 [2 3 1] に対するテンソルベキ表現 T_{[2, 3 1]}:V^⊗n→V^⊗n の古典的書き表し方は、3つのデルタ記号 $\delta^j_\alpha, \: \delta^k_\beta, \: \delta^i_\gamma$ を適当に並べた形になります。

「なんでこんなことするのぉ!?」と思いませんか？それは、「こうすれば計算がうまくいく」からです。現時点で（後知恵で）考えれば、「こんなことしなくても計算はうまくいく」のですけどね。

なぜ、こんな書き表し方が採用されたのか

こんな変な書き表し方を使う気はないし、知る必要もない -- という方は、この先を読む必要はありません。実際、積極的に使う理由は何もありません。しかし、既に使われているものを解釈するためには知っておいたほうがいいでしょう。

まず、最初に注意すべきは、上下の添字がインデックス（番号による成分へのアクセス目的）として使われているとは限らないことです。添字〈サブスクリプトとスーパースクリプト〉が、テンソル（と呼ばれる線形写像）のタイプ情報〈プロファイル情報〉を注釈〈アノテート〉するために使われていることがあります。このことに関しては、次の記事で詳しく解説しています。

テンソル記法の「意味不明問題」は解決した

置換（のテンソルベキ表現）に登場する添字は注釈目的です。つまり、添字は、上記の記事でマーカーと呼んだものです。

今、マーカーを次のように約束したとします。

marker i, j, k for V
marker α, β, γ for V
marker p for W

これは次の意味です。

文字 i, j, k は、ベクトル空間Vを意味する。
文字 α, β, γ は、ベクトル空間Vを意味する。
文字 p はベクトル空間Wを意味する。

さらに、番号と文字との対応も約束します。

i と α は、番号 1 を意味する。
j と β は、番号 2 を意味する。
k と γ は、番号 3 を意味する。

番号との対応の約束から、 $\delta^j_\alpha \delta^k_\beta \delta^i_\gamma$ が、置換（のテンソルベキ表現）T_{[2 3 1]}を表すことが了解できます。

線形写像 x:W→V $\otimes$ V $\otimes$ V を考えます。線形写像 x のプロファイル「W→V $\otimes$ V $\otimes$ V」を、マーカー添字を使って注釈すると：

$x = x^{\alpha\, \beta\, \gamma}_p$

2つの線形写像の結合〈合成〉 x;T_{[2 3 1]} = T_{[2 3 1]} $\circ$ x : W→V $\otimes$ V $\otimes$ V を、古典テンソル記法で書き表すことを考えます。古典テンソル記法では、写像の結合を直接表す方法はなくて、写像のテンソル積と縮約の組み合わせで表します。f := T_{[2 3 1]} と置くならば：

f $\circ$ x = (f $\otimes$ x の縮約)

写像のテンソル積は横併置で表します。縮約を記号的に表すには、同じ名前の添字を対角に配置するという方法を取るのでした（「テンソル記法の「意味不明問題」は解決した」参照）。マーカーとしての添字を使って：

$f\circ x = f^{i\, j\, k}_{\alpha\, \beta\, \gamma} \; x^{\alpha\, \beta\, \gamma}_p$

しかしこれでは、fが置換を実行している事実がまったく伝わりません。次のように書けば、置換が実行されている感じが多少伝わります。

$f^{j\, k\, i}_{\alpha\, \beta\, \gamma} \; x^{\alpha\, \beta\, \gamma}_p = x^{j\, k\, i}_p$

右辺に出てきた $x^{j\, k\, i}_p$ は、もとの写像 $x^{\alpha\, \beta\, \gamma}_p$ に置換 T_{[2 3 1]}を施した〈後結合した〉ものを表すことになります。この時点で「マーカーは注釈」という原則は破られています。マーカーを取り除けば x = x ですが、左辺のxと右辺のxは別物なので、マーカーは違いを識別する目印に使われています。

クロネッカーのデルタに関する規則 $\delta^i_{\alpha} \; x^\alpha = x^i$ などを繰り返し使っていいことにすれば、次のような書き方が“整合的”(?)となります。

$\delta^j_\alpha \delta^k_\beta \delta^i_\gamma \; x^{\alpha\, \beta\, \gamma}_p = x^{j\, k\, i}_p$

以上が、置換のテンソルベキ表現 T_{[2 3 1]} を $\delta^j_\alpha \delta^k_\beta \delta^i_\gamma$ と書き表す事情です。ほとんど手品〈マジック〉の種明かしみたい。ここまでくると、黒魔術〈ブラックマジック〉ですわ。

置換を使った対称化／反対称化オペレータの書き表し方も黒魔術じみています（今日は述べませんが）。当然ですが、モダンな記法を使えば、このような黒魔術を使う必要はまったくありません。歴史的興味とか、趣味的に楽しいとかの理由なら別にとめませんが、もうやめたほうがいいと思います。（と僕が言っても、絶対に滅びないのですが。）

代替となるモダンな書き表し方や、ストリング図による絵図記法〈{graphical | pictorial | diagrammatic} notation〉については、いつか述べたいとは思っています（いつになるかは分からんが）。

*1:普通の人は、ツビタノビッチの方法に驚愕するでしょう。

*2:{1, 2, ..., n} の代わりに一般的な有限集合を考える場合もあります。

*3:例えば、置換全体は対称群で、その部分群を置換群、とか。

*4:Vⁿは、V×...×V なので、ベクトル空間としては直和で Vⁿ = V $\oplus$ ... $\oplus$ V