騙されるな、接続係数（クリストッフェル記号）の仕掛け - 檜山正幸のキマイラ飼育記 (はてなBlog)

「コジュール接続の圏」で、共変微分の話をしました。そこで次のようなことを書きました。

選んだひとつの共変微分に対する、他の共変微分の“差分”（End1Form(E)_Ab の要素）がいわゆる“接続係数”を定めます。ただし、共変微分の空間 CovDer(E) には、特別な基準点は存在しません。一様というかノッペラボウ。

「いわゆる“接続係数”」という言い方 -- これはね、接続係数って誤解されている気がするんですよ。接続係数は差分なんだけど、差分とは思ってない人がいそうです。

単一の共変微分があっても、それから接続係数を決めることはできません。
2つの共変微分があってはじめて、差分としての接続係数を定義できます。

てなことをこの記事に書きます。「コジュール接続の圏」を読んでいる必要はありません。

内容：

設定と約束
接続係数
フレームが決める標準共変微分
書き方の注意
フレームの取り替え
おわりに

設定と約束

共変微分を接バンドルに限る必要はないので、一般のベクトルバンドルE上の共変微分を考えます。

Eの底空間はMとします。Mの次元は m 。どうでもいい話だけど、M, m と大文字・小文字を揃えたかった。
ベクトルバンドルEの階数〈ファイバー次元〉は r とします。
文字'Γ'は、バンドルのセクション空間を表すのに使います。接続係数をΓと書く習慣がありますが、記号がかち合うので、接続係数は A, B などにします。

記述を簡略にするために、次の略記を使います。

Φ(M) = C^∞(M)
Ξ(M) = Γ_M(TM) = (M上の接ベクトル場の空間)
Ω(M) = Γ_M(T^*M) = (M上の1次微分形式の空間)

Ξ(M)とΩ(M)は、関数の可換環Φ(M)上の加群と考えます。Ξ(M)とΩ(M)は、Φ(M)-加群として双対で、その標準スカラー積を <- | -> で表します。Mの開集合Uに関しても、Φ(U), Ξ(U), Ω(U), <- | -> を使います。

Γ_M(E), Γ_M(U, E) も短く書きたいので、Σ(M), Σ(U) とします。総和記号と紛らわしいですが、'Σ'は sections の S だと思ってください。

Σ(M) = Γ_M(E) = (ベクトルバンドルEのM上のセクションの空間)
Σ(U) = Γ_M(U, E) = (ベクトルバンドルEのU上のセクションの空間)

うまく開集合Uを選んであげると、Σ(U), Ξ(U), Ω(U) すべてが有限階数の自由加群になります。つまり、Σ(U), Ξ(U), Ω(U) それぞれに、Φ(U)-加群としての基底を取れます。加群の基底に1から始まる番号を付けたものをフレーム〈frame〉といいます*1。選んで固定した各加群のフレームを次のように表します。

Σ(U) のフレーム： e₁, ..., e_r
Ξ(U) のフレーム： X₁, ..., X_m
Ω(U) のフレーム： ω¹, ..., ω^m

ここで、X₁, ..., X_m と ω¹, ..., ω^m は互いに相反フレーム〈reciprocal frame〉だとします*2。その意味は：

<ωⁱ | X_j> = δⁱ_j （δはクロネッカーのデルタ）

Uが座標近傍のときは、 $X_i = \frac{\partial}{\partial x^i}, \: \omega^i = dx^i$ と決めることが多いでしょうが、そう決める必要はありません。計算が不便になる（実用上は困る）のを覚悟するなら、X₁, ..., X_m と ω¹, ..., ω^m が相反フレームであるという仮定も不要です。

接続係数

∇をベクトルバンドルE上の共変微分だとします。∇は、ライプニッツ法則を満たすR-線形写像です。∇の代数的な表現に関しては、「双線形写像のカリー化」を読むとよいかも知れません。

多様体全体Mとその一部分Uでは事情が違うので、

$\nabla^M :\Sigma(M) \to \Sigma(M)\otimes_{\Phi(M)}\Omega(M)$
$\nabla^U :\Sigma(U) \to \Sigma(U)\otimes_{\Phi(U)}\Omega(U)$

のように、∇の肩にMやUを付けるべきですが（興味があれば「ビッグサイト微分幾何と自然変換の上付き添字」を）、面倒だから省略します。また、以下では開集合Uに関して話をします（局所的議論）。

共変微分∇は上のような写像だとして、s∈Σ(U), X∈Ξ(U) に対して、

∇_X(s) := (∇s)(X)

と定義します。これは若干イイカゲンな書き方で、右辺の (∇s)(X)（∇s に、Xを入力している）では、∇s を“Xを受け取る関数”とみてますが、それは次の同型を使った同一視をしてます。（R-Lin(-, -) は、R-線形写像の空間。）

$\Sigma(U)\otimes_{\Phi(U)}\Omega(U) \cong \Phi(U)\mbox{-}Lin(\Xi(U), \Sigma(U))$

そして、∇の接続係数Aは、次の等式が成立するように定義します。（1..r = {1, ..., r} です。）

$\mbox{For}\: \beta \in 1..r,\: \nabla_{X_i}(e_\beta) = \sum^{\alpha \in 1..r}_{i\in 1..m} A^\alpha_{\beta\; i} (e_\alpha \otimes \omega^i)$

共変微分∇だけから接続係数Aがちゃんと決まるじゃないか、って？いやいやいや、それは騙されている。 $A = (A^\alpha_{\beta\; i} )^{\alpha \in 1..r}_{\beta \in 1..r,\; i \in 1..m}$ は、∇だけで決まっているんじゃないんですよ。

Σ(U) のフレーム e₁, ..., e_r を選んでいるでしょ。この段階で、基準となる共変微分 ∇' を固定しているのです。接続係数 A は、∇と∇'との差 A = ∇ - ∇' として決まるのです。

フレームが決める標準共変微分

共変微分∇があるとして、セクション s∈Σ(U) を∇で微分したらゼロだったとします。このとき、セクション s は ∇ に関して静止している〈stationary〉といいます。「静止」は物理・力学が起源なんでしょうが、あまり言葉を気にしてもしょうがないです。次の定義（だけ）を頭に入れてください。

sが（∇に関して）静止している :⇔ ∇s = 0

Φ(U)-加群 Σ(U) のフレーム e₁, ..., e_r のメンバーであるすべてのセクションが静止しているとき、このフレームは静止している（静止フレーム〈stationary frame〉だ）といいます。

次に、共変微分は特になくて、フレームありきの状態を考えます。e₁, ..., e_r が Σ(U) = Γ_M(U, E) のフレームです。さて、このフレームを静止させるような共変微分は存在するでしょうか？ ∇' をそうなるように作っちゃえばいいのです。

まず、

∇'(e_α) = 0 （α∈1..r）

e_α に関数 f∈Φ(U) を掛け算した fe_α に関しては、ライプニッツ法則から、
$\:\:\:\: \nabla'(f e_\alpha) \\ = df \otimes e_\alpha + f(\nabla' e_\alpha) \\ = df \otimes e_\alpha$

$df \otimes e_\alpha$ はテンソル積の左右を逆に書いたほうがいいけど、「テンソル積の順序はテキトー」でいいとします。

Eの任意のセクション s∈Σ(U) は、 $s = \sum_{\alpha\in 1..r} f^{\alpha}e_\alpha$ と書けます。その微分は、
$\:\:\:\: \nabla'(s) \\ = \nabla'(\sum_{\alpha\in 1..r} f^{\alpha}e_\alpha) \\ = \sum_{\alpha\in 1..r} \nabla'(f^{\alpha}e_\alpha) \\ = \sum_{\alpha\in 1..r} d(f^{\alpha})\otimes e_\alpha \\$

以上で、 $\nabla' : \Sigma(U) \to \Sigma(U) \otimes_{\Phi(U)} \Omega(U)$ が完全に決まりました。もちろん、∇' に関してフレーム e₁, ..., e_r は静止しています。そうなるように作ったので。こうやって作った共変微分 ∇' をフレーム e₁, ..., e_r の標準共変微分〈canonical covariant derivative〉と呼ぶことにします。

書き方の注意

通常、関数 f∈Φ(U) をベクトル場 X∈Ξ(U) により方向微分したものを Xf = X(f) と書きます。僕、この書き方きらいです。Xにfを掛け算したいとき、右からの掛け算 Xf が禁止されてしまいます。それがイヤッ。

外微分作用素を d:Φ(U)→Ω(U) としたとき、外微分の定義から df(X) = <df | X> は方向微分と同じです。なので、Xf の代わりに df(X) が使えます。とはいえ、方向微分の気分を出したいので、d_Xf = df(X) という書き方も使うことにします。

こうすると、共変微分の書き方と整合します。

共変微分	外微分
$\nabla= \nabla^U\; : \Sigma(U) \to \Sigma(U)\otimes_{\Phi(U)}\Omega(U)$	$d = d^U\; : \Phi(U) \to \Phi(U)\otimes_{\Phi(U)}\Omega(U)$
$\nabla s \in \Sigma(U)\otimes_{\Phi(U)}\Omega(U)$	$d f \in \Phi(U)\otimes_{\Phi(U)}\Omega(U)$
$\nabla_X s = \nabla s(X) \in \Sigma(U)$	$d_X f = df(X) \in \Phi(U)$

計算するときは、次のような同型／同一視を（ときに暗黙に）使います。

$\Phi(U)\otimes_{\Phi(U)}\Omega(U) \cong \Omega(U)$
$\Sigma(U)\otimes_{\Phi(U)}\Omega(U) \cong \Phi(U)\mbox{-}Lin(\Xi(U), \Sigma(U))$
$\Phi(U)\otimes_{\Phi(U)}\Omega(U) \cong \Phi(U)\mbox{-}Lin(\Xi(U), \Phi(U))$
$\Sigma(U)\otimes_{\Phi(U)}\Omega(U) \cong \Omega(U)\otimes_{\Phi(U)}\Sigma(U)$

この書き方と同型／同一視を使って、ライプニッツ法則を幾つかの形で書いてみましょう。

$\nabla(fs) = (df)\otimes s + f(\nabla s)$
$\langle \nabla(fs) \mid X \rangle = \langle (df)\otimes s \mid X \rangle + \langle f(\nabla s) \mid X \rangle$
$(\nabla(fs))(X) = ( (df)\otimes s)(X) + (f(\nabla s))(X)$
$\nabla_X(fs) = (d_X f) s + f(\nabla_X s)$

[追記]
f(...) と書くと、関数fに引数"..."を渡したように見えちゃうなー。関数とセクションの掛け算には、明示的な掛け算記号（ドット）を付けることにすると：

$\nabla(f \cdot s) = (df)\otimes s + f \cdot (\nabla s)$
$\langle \nabla(f \cdot s) \mid X \rangle = \langle (df)\otimes s \mid X \rangle + \langle f \cdot (\nabla s) \mid X \rangle$
$(\nabla(f \cdot s))(X) = ( (df)\otimes s)(X) + (f\cdot (\nabla s))(X)$
$\nabla_X(f \cdot s) = (d_X f)\cdot s + f \cdot (\nabla_X s)$

$\langle \omega \otimes s \mid X \rangle = \langle s \otimes \omega \mid X \rangle = s \cdot \langle \omega \mid X \rangle = \langle \omega \mid X \rangle \cdot s$ とかも使ってますね。厳密に言えばイコールじゃないけど。
[/追記]

フレームの取り替え

Φ(U)-加群 Σ(U) = Γ_M(U, E) のフレームを選ぶと、自動的にベクトルバンドルEの（U上の）標準共変微分を特定したことになります。そして、他の共変微分∇を標準共変微分との差として記述することになります。共変微分∇を別なフレームから見れば、別な見え方になるでしょう。その様子は、次のような絵に描けます。

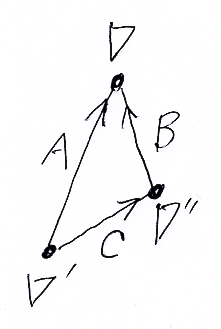
この絵では、共変微分を点で、接続係数（差分）を矢線で表しています。実は雰囲気的な絵じゃなくて、（無限次元空間における）幾何的状況を割と正確に表現した絵なんです。なぜなら、共変微分全体の空間は、E値微分形式*3のアーベル群 Σ(U) $\otimes$ Ω(U) を構造群とする主等質空間であり、実数上のアフィン空間でもあるからです。詳しくは「コジュール接続の圏 // 共変微分の空間」を参照。

もう一度上の絵を見てください； ∇'はフレームの標準共変微分です。∇'から∇を見たときの接続係数（差分）がAです。∇''は別な（第二の）フレームの標準共変微分だとします。∇''から∇を見たときの接続係数（差分）がBですね。そして、2つのフレームの標準共変微分の差＝接続係数がCです。次の関係は明らかでしょう。

C + B = A
B = -C + A = A - C

接続係数Aが分かっている状況で、第二のフレームによる接続係数Bを計算したいなら、∇'から見た∇''の接続係数Cを求めて引き算すればいいのです。

C = ∇'' - ∇' を求めましょう。∇'を決めているフレームを e_α（α∈1..r）、∇''を決めているフレームを g_γ（γ∈1..r）とします。フレーム e_α とフレーム g_γ は、Φ(U)係数のr×r行列でお互いに移りあえるはずです。

$g_\gamma = \sum T_\gamma^\alpha e_\alpha$
$e_\alpha = \sum S_\alpha^\gamma g_\gamma$

$T = (T_\gamma^\alpha)_{\gamma \in 1..r}^{\alpha \in 1..r},\; S = (S_\alpha^\gamma)_{\alpha \in 1..r}^{\gamma \in 1..r}$ は、関数（Φ(U)の要素）係数の正方行列で、互いに逆行列になっています。

第一のフレーム	第二のフレーム
$e_\alpha \:(\alpha \in 1..r)$	$g_\gamma \:(\gamma \in 1..r)$
標準共変微分 $\nabla'$	標準共変微分 $\nabla''$
$\nabla' e_\alpha = 0$	$\nabla'' g_\gamma = 0$
$e_\alpha = \sum S_\alpha^\gamma g_\gamma$	$g_\gamma = \sum T_\gamma^\alpha e_\alpha$

∇'から見た∇''の接続係数（差分）Cは、次の等式で規定されるのでした。

$\nabla'' e_\beta = \sum C_{\beta\; i}^{\alpha} (e_\alpha\otimes \omega^i)$

接続係数Cを別な方法 -- 行列による変換にライプニッツ法則を適用する方法で計算してみます。
$\:\:\:\: \nabla'' e_\beta \\ = \nabla'' (\sum S_\beta^\gamma g_\gamma) \\ = \sum \nabla''(S_\beta^\gamma g_\gamma) \\ = \sum ( (dS_\beta^\gamma) \otimes g_\gamma + S_\beta^\gamma(\nabla'' g_\gamma)) \\ = \sum ( (dS_\beta^\gamma) \otimes g_\gamma) \\ = \sum ( (dS_\beta^\gamma) \otimes \sum T_\gamma^\alpha e_\alpha) \\ = \sum ( (dS_\beta^\gamma) \otimes T_\gamma^\alpha e_\alpha) \\ = \sum ( (dS_\beta^\gamma)T_\gamma^\alpha \otimes e_\alpha)$

ここで、総和は上下に出現する添字に渡って取る、というルールを使っています。まだ、計算は終わっていません。一般に、関数の外微分 df は次の表示を持ちます。

$df = \sum (d_{X_i}f) \omega^i$

局所座標から誘導されるフレームの場合はお馴染みでしょう。

$df = \sum (\frac{\partial f}{\partial x^i}) dx^i$

$dS_\beta^\gamma = d(S_\beta^\gamma)$ をこの表示で展開して：

$dS_\beta^\gamma = \sum (d_{X_i}S_\beta^\gamma) \omega^i$

これを使って計算を続けます。
$\:\:\:\: \sum ( (dS_\beta^\gamma)T_\gamma^\alpha \otimes e_\alpha) \\ = \sum ( (\sum (d_{X_i}S_\beta^\gamma) \omega^i)T_\gamma^\alpha \otimes e_\alpha) \\ = \sum ( \sum (d_{X_i}S_\beta^\gamma) T_\gamma^\alpha) ( e_\alpha \otimes \omega^i)$

以上で、テンソル積加群の二重添字フレーム $e_\alpha \otimes \omega^i$ （α∈1..r, i∈1..m）に関して、Cの成分表示が2種類得られたので、これらを比較すれば：

$C^\alpha_{\beta\;i} = \sum (d_{X_i}S_\beta^\gamma) T_\gamma^\alpha$

おわりに

記事タイトルに出した（第二種の）クリストッフェル記号とは、リーマン多様体Mの接バンドルTMの、計量から導かれる共変微分∇の接続係数のことです。接バンドルのフレーム（通常は局所座標から作られるフレーム）を選ぶと標準共変微分が決まるので、それに対する∇の接続係数＝差分の成分表示が、クリストッフェル記号ですね。

特別な状況を仮定しない一般的なベクトルバンドルでは、局所座標／局所座標から作られるフレーム／計量などと関わりがありません。色々な概念が一緒に入り込むと、どうしてもゴチャゴチャになるので、プレーンなベクトルバンドルの共変微分を調べておくほうがクリアな理解が得られる気がします。

*1:Φ(U)-加群Σ(U)のフレームとは、ベクトルバンドルEのフレーム場（あるいはフレームセクション）です。それはまた、Eのフレームバンドル frame(E) のセクションでもあります。

*2:双対フレームと呼ばれることが多いですが、普通の意味の双対じゃないので「相反」とします。

*3:ベクトルバンドル（のセクション）が係数となる微分形式の書き方は色々あって分かりにくいですね。必要があれば「拡張された係数を持つ微分形式の空間の書き方」を参照してください。