このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

カリー／ハワード（Curry-Howard）の対応を知らない子ども達および大人達へ

雑記／備忘

3月19日(木)にやったセミナーに関して、さっそくにKuwataさんによるまとめが公開されています。

これがまた、とんでもない力作で驚きました。とてもよく仕上がったレポートで、僕の話なんかより、これを読んだほうが分かりやすいくらい。ホントにお疲れさま。どうもありがとう。

Kuwataさん曰く：

今回は内容的に俺がまとめを書けるレベルじゃねえと思っていたら、他の参加者から「また徹夜してまとめ書くんでしょ」と言われてもう後に引けない状況。

僕も含めて皆さん期待していたのは確か。「まとめるんだよね、帰ったら書くんだよね、朝まで書くんだよねー」と、何人かがKuwataさんに声をかけていたけど、彼を殺してしまいかねないから、もうあまり言わないように。

Kuwataさん曰く：

さすがに仕事帰りにセミナー寄って、そっから4時間半ぶっ続けで執筆というのは無謀過ぎた。

僕より誰より、一番消耗したのはKuwataさんだったね。無理をし過ぎないように。長生きしてね、Kuwataさん。


さて、Kuwataレポートの流れに沿いながら、当日説明不足だった事、あるいはまったく触れなかった事などを補足していくことにします。

※ このエントリーのタイトルは、 http://d.hatena.ne.jp/nobsun/20070915/p2 にインスパイアされました。

内容：

はじめに

Kuwataさんに刺激され、僕もこの長いエントリーを書きました。Kuwataさんのレポートと、当エントリーにより、「技術者／プログラマのためのラムダ計算、論理、圏」セミナー第3回の雰囲気と内容を、かなりの程度伝えることができるだろうと思います。


参加者のみなさんの様子や質問などを思い起こして、今までの説明で腑に落ちなかった（と思える）内容に追加説明を加えるようにしました。例えば、大きなラムダ式と小さなラムダ式を区別することに疑問を感じた方がいると思います。その疑問への答は、「まったく違うものだから違う記法を採用した」なのですが、このエントリーの最後のほうを読めば、おそらくは納得いただけると思います。

算術計算図、証明図、証明可能性

Kuwataさん曰く：

まず算術回路・算術計算図という代物を使った計算過程の視覚化のトレーニングを行い、

算術計算図は、証明図（proof-figure）に入る前のトレーニング目的で僕が考案したもので、足し算は次のように書きます。

  2   3
 -------[+]
    5

証明図の「∧-導入の規則」は次の形です。

  A    B
 ---------[And]
   A∧B

算術演算と推論の違いはあれど、どちらも次の状況を表現します。

  入力1  入力2
 --------------[操作]
     出力

上の足し算の図が表す内容を 2 + 3 = 5 と書くのと同様に、「∧-導入の規則」の図が表す内容を

  • A, B |- A∧B

とも書きます。ここで出てきた「|-」（ターンスタイル記号）の意味は、

  • 左側の論理式を仮定して、右側の論理式（結論）に至る証明図が作れる

です。もっと短く言えば、

  • 左側の仮定から、右側の結論を証明できる

となります。

いままさに述べているようなことを、違和感なく受け入れるには、「仮定、結論、推論、証明」などを 外側から超越的に眺めること、対象物としてクールに取り扱うことが必要です。「証明できる」は、与えられたシステム（演繹系）の性質を述べているのであって、主語が「私」ではありません。

「証明できることを証明できる」という主張は、ちゃんと主語を書くと、次のような意味です。

  • 与えられた演繹系を使って、ある論理式を結論とする証明図が描けることを、私は（あるいは誰かが）明確に示すことができる。

同じことを算術（算数）に関して言えば、

  • 与えられた算術系（算術計算のシステム）を使って、ある数を算出する計算図が描けることを、私は（あるいは誰かが）明確に示すことができる。

特に変なことをは言ってないでしょ。算術的計算も論理的証明も、同じ態度で扱い考えることが重要なのです。

Kuwataさん曰く：

算術計算図を重点的に使う。理由は算術計算図はテキストエディタだけでも気合で書けるからだ。

本や論文において、ボックス（あるいはオダンゴ）とワイヤーを使った図より証明図が多用されるのは、文字組版の範囲で制作・印刷できるからでしょう。ただ、ワイヤーがない分だけレイアウトが大変です。慣れないと、何度も描き直すハメになります。（ちなみに、id:oto-oto-otoさんが、証明図のレイアウトを支援するソフトウェアを使ったことがあるとおっしゃっていました。）

最近使われるようになった証明ネット（↓）だともう、テキストエディタや文字組版では無理で、図版として描くしかないですね。頭が痛い問題です。

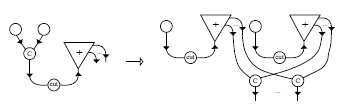
構造規則に関して色々

Kuwataさん曰く：

推論規則とは別に構造規則というものもある。

僕、そんな言い方をしたのかもしれませんが、事実はちょっと違います。構造規則も推論規則の一種です。推論規則を次の2種に分類するのです。

  • 論理記号を導入、消去するタイプの規則 -- 論理規則
  • それ以外 -- 構造規則

実際に使われる可能性がある構造規則は次の3つです。

    A
 -------[複製 Duplicate]
  A   A  


  A   B
 -------[入れ替え Exchange]
  B   A

  
   A
 -----[破棄 Discard]

3番目の、仮定を捨ててしまう規則は、今回使いませんでした。あれば便利なときもありますが、分かりにくくなる点もあるのであえて禁止しました。

仮定Aを捨てたいときは次のようにします。

   A    B
 ----------[And]
    A∧B
  --------[Sel-2]
     B

Aを捨てるための相方（悪役？）としてBを持ち出しています。この過程でBには何の影響もありません。もって回った方法ですが、Aの破棄に使えることは確かです。例として、(A⊃(B⊃A) の証明図（描き上がり）を挙げておきます。Sel-1のところでBを捨てています。しかし、含意（⊃）の左側にBを埋め込んで使っているので、捨てたBも無意味ではないのです。

 #2    #1
 ---  ---
  A    B
 --------[And]
   A∧B
  ------[Sel-1]
    A
  ------[DT #1]
   B⊃A
  --------[DT #2]
 A⊃(B⊃A)

なお、Duplicate, Discard, Exchangeには、「増」、「減」、「換」という漢字1文字による訳語があります。セミナー内ではこの訳語を使わなかったのですが、しゃれていて、僕は好きです。言葉の問題は「Δとσはこんなにいろいろな言い方がある」にもメモしてあります。

実際に証明図を描いてみると、コピー（Duplicate, Dup）が思いのほか多用されているのがわかります。コピーにはコスト（リソース、エネルギー）がかかる点に注意してください。破棄（Discard）にもコストがかかります。計算や推論におけるコストの問題は、次のエントリーで扱っています。

構造規則に関してもっと色々

入れ替えは、ワイヤーで描けばこんな感じ（↓）。

＼　　／
　＼／
　／＼
／　　＼

2回続けて入れ替えるともとに戻ります。

＼　　／
　＼／
　／＼
／　　＼
＼　　／
　＼／
　／＼
／　　＼
これは証明図

  A   B
 -------[Exch]
  B   A
 -------[Exch]
  A   B

しかし、入れ替えの交差（X形）が、＼が上のヤツと／が上のヤツの二種類あったらどうでしょう。

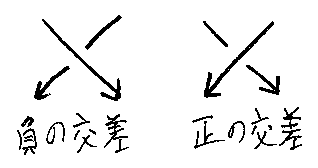
同じ入れ替えを2回続けても、ヒモがからむので、もはやもとに戻りません。正負の入れ替え交差を組み合わせると、例えば次のような図が出来上がります。

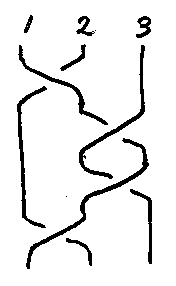
そう、これはブレイド（組み紐）の話です。ブレイドに、∩形や∪形にカーブしたヒモを許すと結び目を作れます。絵で「カーブしたヒモを許す」あるいは「ヒモをカーブさせてもいい」ということは、計算においてラムダ抽象（カリー化）を許すことです。カリー／ハワード対応で証明の世界に行けば「含意の導入規則を許す」ことですよね。

つまり、入れ替えの構造規則をわずかに変える（ワイヤーの交差を立体交差にする）だけで、証明図がブレイドや結び目に様変わりします。ワイヤー（ヒモ）を、粒子の運動軌跡だと思うと、古典的あるいは相対論的な時空図やファインマン図だとも解釈できます。

ここらへんが、論理の証明論が、結び目のトポロジーや場の量子論と直結する背景だろうと思います。（実はよくは分かってないけど、「バエズとステイのロゼッタストーン論文と現代のヒエログリフ」とかも参照。）

常識的な省略とマクロ推論規則

Kuwataレポートに戻って、Kuwataさん曰く：

この図[檜山注：連立1次方程式を解く図]を見てドン引きしてる人もいるかもしれないけど、セミナーではマジでこういう図を手書きしてたんだよ

Kuwataさんの図で、横線の右に何の注釈も書いてないのはマクロ推論規則になります。実際には、等式に関する公理や規則、加減乗除の性質を表す公理などを使った証明過程が省略されています。それらの証明を律儀に書き下すと、図はもっともっと大きく膨れあがります。高級言語の数行のソースコードでも、最終的に実行される機械語の列が長くなるのと同じです。

実際に我々が行う行為としての証明（方程式を解くことも証明）では、「等式に関する移項」のようなマクロな規則や、既に証明された結果（それが定理）をヘビーに使っているのであって、毎回毎回、公理と基本推論規則に戻っているわけではありません。算術計算とのアナロジーで言えば、「マクロな規則の使用≒関数／マクロの呼び出し」、「定理の引用≒計算済み定数を直接書くこと」となります。

含意に関して色々

Kuwataさん曰く：

ここで「ならば」に相当する記号「⇒」を導入する。セミナーでは別の記号が使われていたけど、俺の使ってるフォントにはその記号が無いのでご勘弁。

記号は別にどうでもいいのですが、僕が「⊃」を使ったのは、「⊃」が一番よく使われているように思えることと、「→」、「⇒」が他の目的にもよく使われるので混乱を避けるためです（「論理記号のいろいろ」を参照）

含意の導入規則（演繹定理そのもの）は、なかなか分かりにくいと思います。含意が日常語の「ならば」とズレがあるし、さまさまレベルでの「ならば」があるのです（詳細は「さまざまな「ならば」達」を参照）。

僕はさらに、次のことが含意導入を分かりにくくさせている気がします。それは、非常に多くの解説が「証明図は証明を表す」と言っていることです。違います。証明図は単に証明行為のスナップショットです。証明とは、証明図を描き変えていく全過程を意味するのです。図の描き換え／変更が全て終わった最後の図を分析すると、描き変えてきた全過程が分かるので「証明図は証明を表す」と言えなくもないでしょうが、証明をアニメーションやムービーと考える観点はとても重要です。

含意導入の例を、下に示します。含意導入の前後で証明図全体が大幅に書き変わるのです。

書き換える前（A, B |- B）
  A   B
 --------[And]
   A∧B
 -------[Sel-2]
    B

書き換えた後（A |- B⊃A）
     #1
     ---
  A   B
 --------[And]
   A∧B
 -------[Sel-2]
    B
 ------[DT #1]
  B⊃A

もっと書き換えた後（|- A⊃(B⊃A)）
 #2  #1
 --- ---
  A   B
 --------[And]
   A∧B
 -------[Sel-2]
    B
 ------[DT #1]
  B⊃A
 ---------[DT #2]
 A⊃(B⊃A)

出来上がった最終的証明図を上から下に読んでも分かりにくいのは、上から下の順で描かれたのではなくて、まん中へんから上下に伸びて作られたものだからです。証明図が育っていく過程は非常に複雑になり得ます。上から下に育つとは限りません！ このことは、自然演繹方式の欠点でもありますが、「人間の思考過程に近い」とも言えるのではないでしょうか。

また、証明を動的過程（運動）と捉えることは、証明論と、幾何学的グラフ理論／グラフ書き換え系（graph rewriting system）を関連付けるさいの本質的視点でもあります。

三段論法って何？

Kuwataさん曰く：

所謂「ソクラテスは人間だから死ぬ」とかの三段論法の事らしい。

そうです。「所謂＜いわゆる＞三段論法」です。が、当日も注意したように、「三段論法」は俗語ですから、「所謂」を付けて使用すべきでしょう。三段論法の正式な意味は、おそらく、大昔にアリストテレスが提唱した推論規則群のことだと思います。それは、モダスポネンスやカット（下に紹介）とは違います。

  A⊃B   A
 ----------[モダスポネンス]
     B


 A⊃B  B⊃C
 ----------[カット（Cut）]
   A⊃C

選言に関する推論規則

選言（Or, ∨）はセミナー当日は触れませんでした（使わないので）。が、Kuwataさんは触れています。

Kuwataさん曰く：

導入：
 A 　 B
 ------ [Or]
 A ∨ B

これ、ちょっと違います。A∨B を言うのに、AとBの両方は必要ないので、次のようになります。

導入その1：
   A
 ------ [Or-1]
  A∨B

導入その2：
   B
 ------ [Or-2]
  A∨B

そして、連言の消去。Kuwataさん曰く：

消去：
 A ∨ B     A ⇒ C   B ⇒ C
 ---------------------------
           C

これはOKです。次のように、含意を入れないほうが使いやすいかも。

書き換え前
         A      B
   :     :      :
   :     :      :
  A∨B   C      C

書き換え後
        #1     #2
        ---    ---
         A      B
   :     :      :
   :     :      :
  A∨B   C      C
 ----------------[Case #1, #2]
        C

#1と#2は、含意導入と同じように、AとBを証明の仮定から外すときの整理番号です。#1から下に流れる部分は「Aの場合」、#2から下に流れる部分は「Bの場合」という、場合分け分析（case analysis）です。この推論を使うときは、A∨B が出た後で、横に「Aの場合」と「Bの場合」の証明を建て増しします。このときも、証明図は上から下へとは育ちません。

ズバリ、これがカリー／ハワード対応だ

Kuwataさんが彼のレポートの最後に描いた図を素材に、カリー／ハワード対応（Curry-Howard Correspondence）を最後まで追いかけてみます。ただし、タプルを作る操作が「t」なのは、記号の整合性から気持ち悪いので「Tup」とします。

まずは論理側での、(A∧B)⊃C |- A⊃(B⊃C) の証明。

ここらへんからスタート：
             A    B 
            --------[And]
  A∧B ⊃ C   A∧B
 --------------------[MP]
         C

⊃導入：
                 #1
                 ---
             A    B 
            --------[And]
  A∧B ⊃ C   A∧B
 --------------------[MP]
         C
     -------[DT #1]
       B⊃C

もういっちょ⊃導入：
            #2    #1
            ---  ---
             A    B 
            --------[And]
  A∧B ⊃ C   A∧B
 --------------------[MP]
         C
     -------[DT #1]
       B⊃C
    ----------[DT #2]
     A⊃(B⊃C)

これは、(A∧B)⊃C, A, B |- C の証明図からスタートして、(A∧B)⊃C |- A⊃(B⊃C) の証明図を描いていますね。もう一歩進めれば、 |- ((A∧B)⊃C)⊃(A⊃(B⊃C)) という仮定なしの証明も得られます。

さて今度は、A, B, Cを型名だと思い、適当な変数を割り当てていきます。それと、「∧」をタプル構成に、「⊃」を関数型を構成する「->」に一斉に置き換えます。モダスポネンスMPの代わりのAppは関数適用、演繹定理DTの代わりのCurrはカリー化です。

ここらへんからスタート：
               x:A     y:B 
               --------------[Tup]
 f:(A, B)->C   (x, y):(A, B)
 ----------------------------[App]
       f・(x, y):C

カリー化：
                       #1
                       ---
               x:A     y:B 
               --------------[Tup]
 f:(A, B)->C   (x, y):(A, B)
 ----------------------------[App]
       f・(x, y):C
      -----------------------[Curr #1]
      λy.(f・(x, y)):B->C

もういっちょカリー化：
               #2      #1
               ---     ---
               x:A     y:B 
               --------------[Tup]
 f:(A, B)->C   (x, y):(A, B)
 ----------------------------[App]
       f・(x, y):C
      -----------------------[Curr #1]
      λy.(f・(x, y)):B->C
     ---------------------------[Curr #2]
     λx.λy.(f・(x, y)):A->(B->C)

これはですね、型付きの大きなラムダ式 <x:A, y:B | f・(x, y) :C> からスタートして、そのフルカリー化 ΛΛ<x:A, y:B | f・(x, y) :C> を計算していることになります。

   ΛΛ&lt;x:A, y:B | f・(x, y) :C>
 = Λ&lt;x:A | λy.(f・(x, y)) :B->C>
 = &lt;| λx.λy.(f・(x, y)) :A->(B->C)>

実際には、fも変数ですから、次のようです。

   ΛΛ&lt;f:(A, B)->C, x:A, y:B | f・(x, y) :C>
 = Λ&lt;f:(A, B)->C, x:A | λy.(f・(x, y)) :B->C>
 = &lt;f:(A, B)->C | λx.λy.(f・(x, y)) :A->(B->C)>

fが大きなラムダ式の引数に残っていることは、先の証明図で (A∧B)⊃C が仮定に残っていたことに対応します。fもカリー化して内部に繰り込むと、閉じたラムダ式が出来ます。

ここまで書けば、大きなラムダ式と小さなラムダ式を区別した理由は明らかですね。

  • 大きなラムダ式：証明図／計算図全体の機能を表す
  • 小さなラムダ式：証明図／計算図に現れる論理式／項を表す

デカルト閉圏（セミナー内では説明できませんでした）との関係で言えば：

  • 大きなラムダ式：デカルト閉圏の任意の射を表す
  • 小さなラムダ式：デカルト閉圏の終対象1からの射を表す。

特に集合圏では：

  • 単元集合1から集合Sへの射と、集合Sの要素は1：1に対応する

すなわち、「<| ナニカ>」と「ナニカ」を同一視することが許されるので、

  • 小さなラムダ式：関数をコード化したデータを表す。

とも言えます。

最後に

セミナーでは、それぞれの話題を解説するのでイッパイイッパイで、相互の関係を述べる余裕がほとんどありませんでした。例えば、プログラムの停止性の問題とカリー／ハワード対応は、ある文脈内ではつながります。直接的な続きの話（シリーズ第4回）はもうありませんので、それぞれの話題を結び合わせる補足は、あと1, 2回エントリーを書いてサポートしたいと思います。