「指標の話: 形状の記述と形状付き集合」において、形状付き集合について述べました。よく使われる形状付き集合に球体集合〈球体的集合〉があります。球体集合達の圏の部分圏(有限な球体集合達)に対して、その構文表示を考えましょう。
圏の構文表示とは、当該の圏を、形式的体系から規準的に作られる圏として表示することです。ここでは、型理論のマナーに従った形式的体系〈型システムの構文論パート〉により、有限な球体集合達の圏を表示してみます。この記事で、有限な球体集合達の圏を定義して、引き続く記事でその構文表示を組み立てます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} } %use
\newcommand{\In}{\text{ in }}
\newcommand{\id}{ \mathrm{id} } % use
\newcommand{\twoto}{ \Rightarrow } % use
\newcommand{\o}[1]{ \overline{#1} }
\newcommand{\Imp}{\Rightarrow}
%\newcommand{\hyp}{\text{-} }
\newcommand{\H}[1]{ {#1}\text{-} }
%%
\require{color} % Using
\newcommand{\NN}[1]{ \textcolor{orange}{\text{#1}} } % New Name
\newcommand{\NX}[1]{ \textcolor{orange}{#1} } % New EXpression
\newcommand{\T}[1]{\text{#1} }
`$
内容:
続きの記事:
ハブ記事:
圏の構文表示
形式言語理論、論理、型理論などは形式的体系〈formal system〉を扱います。形式的体系とは、記号の組み合わせであるデータ(構文的データ)と、そんなデータに対する機械的操作達からなる構造物です。こう言っても曖昧で漠然としてますが、なにかしらの形式的体系達の集合 $`\mathscr{A}`$ があるとしましょう。集合 $`\mathscr{A}`$ に属する形式的体系は、$`A, B`$ などで表します。極端な例としては、集合 $`\mathscr{A}`$ は唯一つの形式的体系しか含まないこともあります; $`\mathscr{A} = \{A\}`$ 。
小さい圏達の厳密2-圏を $`{\bf Cat}`$ 、大きい圏達の厳密2-圏を $`{\bf CAT}`$ とします。形式的体系達の集合から、小さい圏または大きい〈小さいとは限らない〉圏を作り出す手続きがあったとして、それを次のように書きましょう。
$`\quad \mrm{SynCat} : \mathscr{A} \to |{\bf Cat}| \In {\bf SET}\\
\quad \mrm{SynCAT} : \mathscr{A} \to |{\bf CAT}| \In \mathbb{SET}
`$
白抜き文字の SET については、「変換手意味論とブラケット記法 // n-圏」とそこからのリンク先をみてください。
構成手続き $`\mrm{SynCat}`$ が与えられている状況で、$`\mrm{SynCat}(A)`$ は、形式的体系 $`A`$ の構文圏〈{syntactic | syntactical} category〉と呼びます。サイズが大きい $`\mrm{SynCAT}`$ のときも構文圏の定義は同様です。なお、言語理論などの syntactic category は統語範疇〈文法範疇〉の意味でまったく別な概念のことですから注意してください。
圏 $`\cat{C} \in |{\bf Cat}|`$ が、適当な形式的体系 $`A`$ により、
$`\quad \cat{C} \cong \mrm{SynCat}(A) \In {\bf Cat}`$
($`\cong`$ は圏同値)と書けるとき、$`A`$ と $`\mrm{SynCat}`$ の組み合わせを、圏 $`\cat{C}`$ の構文表示〈syntactic presentation〉と呼びます。同じことですが、$`\cat{C}`$ は $`A, \mrm{SynCat}`$ により構文的に表示される、とも言えます。$`\mrm{SynCAT}`$ のとき(サイズが大きいとき)も同じです。
$`\mathscr{A}`$ が単なる集合ではなくて、形式的体系のあいだの準同型射〈homomorphism〉を備えた圏となり、$`\mrm{SynCat}`$(あるいは $`\mrm{SynCAT}`$)が関手になるとより便利ですが、今日のところは、$`\mathscr{A}, \mrm{SynCat}`$ を単なる集合と写像として考えます。
圏の構文表示の実例として、有限球体集合達の圏 $`{\bf Fin}\H{{\bf G}}{\bf Set}`$ を、型理論の形式的体系 $`\mathsf{Glob}`$ により構文表示する手続き
$`\quad \mathsf{Glob} \mapsto \mrm{SynCAT}(\mathsf{Glob}) \cong {\bf Fin}\H{{\bf G}}{\bf Set}`$
を、この記事と引き続く記事で組み立てます。
この構文表示の例は、「指標の話: ペースティング図とバタニン・ツリー」でも引用したフィンスター/ミムラムの論文に書いてあることです。が、用語・記法は変更しています。
- [FM17-]
- Title: A Type-Theoretical Definition of Weak ω-Categories
- Authors: Eric Finster, Samuel Mimram
- Submitted: 9 Jun 2017
- Pages: 12p
- URL: https://arxiv.org/abs/1706.02866
組み合わせ構造を持つ球体
0次元の球体とは、一点のことです。1次元の球体とは、両端がある線分〈閉区間〉のことです。2次元の球体とは、円周を境界とする円板です。3次元の球体とは、球面を境界とする通常の意味の球体です。
(n -1)次元の球面を境界とするn次元の球体は、次のような点集合として定義できます。
$`\quad \{(x_1, \cdots, x_{n}) \in {\bf R}^{n} \mid x_1^2 + \cdots + x_{n}^2 \le 1\}`$
ここで考える球体は、単なる点集合ではなくて、組み合わせ構造を持ちます。n次元球体の境界は、2つの(n -1)次元球体を、(n -2)次元球面を糊しろとして貼り合わせて作った、と考えます。2008年の記事「おとぎ話としてのn-圏 -- 計算できる図形達の世界」の絵をそのまま再掲します。

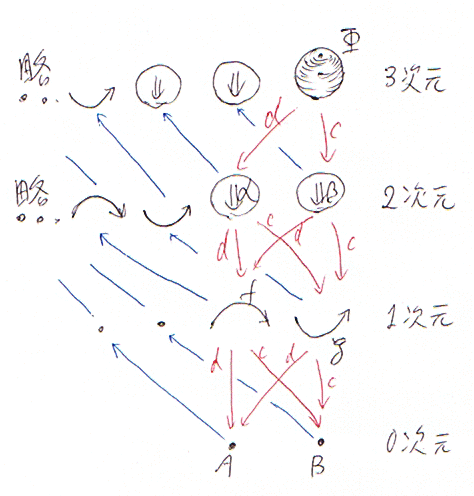
- 3次元球体 $`\Gamma`$ の境界は、2つの2次元球体〈円板〉 $`\alpha`$(図で上側)と $`\beta`$(図で下側)からなります。
- 2次元球体 $`\alpha`$ の境界は、2つの1次元球体〈閉区間〉 $`f`$(図で上側)と $`g`$(図で下側)からなります。
- 1次元球体 $`f`$ の境界は、2つの0次元球体〈点〉 $`A`$(図で上側)と $`B`$(図で下側)からなります。
- 0次元球体 $`A`$ の境界は、便宜上、2つの(しかし一致する)(-1)次元球体 $`*`$ からなります。
(-1)次元球体は、モノイド積を考えるときは便宜上ではなくなり(実体を持ち)ますが、今は単なるダミーの記号だと思ってください。
これ以降、組み合わせ構造を持ったn次元球体を単に(n次元の)球体〈globe〉と呼びます。球体の境界は1次元低い次元の2つの球体になりますが、片一方の境界球体からもう一方の境界球体への向きを持つとします。片一方の境界球体を始面〈source face〉、もう一方を終面〈target face〉と呼びます。
球体にその始面を対応させる写像を source, src, s, dom, d などの綴りで呼びます。球体にその終面を対応させる写像は target, trg, t, cod, c などの綴りです。人により場合により使われる綴りは色々です。
以下の図は2008年の記事「バタニンの球複体 とりあえず導入」の絵で、始面写像を d 、終面写像を c で表しています。青い矢印は、退化写像〈degeneracy map〉と呼ばれる写像ですが、今回は関係ないので無視してください。赤い矢印だけ見ましょう。あと、3次元球体の名前はなぜか($`\Gamma`$ じゃなくて)$`\Phi`$ になってます -- なんかの気まぐれです。
最近(2024年5月)の記事「等式的2-グラフ(2-圏の記述のために) // セルのプロファイルグラフ」においても、同様な話をして、説明のためにプロファイルグラフという図を描いています。
$`\quad \xymatrix{
{}
& {_3 x} \ar@{|->}[dl]_s \ar@{|->}[dr]^t
& {}
\\
{_2 x^{(1)}_-} \ar@{|->}[d]_s \ar@{|->}[drr]^>>t
& {}
& {_2 x^{(1)}_+} \ar@{|->}[dll]_>>s \ar@{|->}[d]^t
\\
{_1 x^{(2)}_-} \ar@{|->}[d]_s \ar@{|->}[drr]^>>t
& {}
& {_1 x^{(2)}_+} \ar@{|->}[dll]_>>s \ar@{|->}[d]^t
\\
{_0 x^{(3)}_-} \ar@{|->}[dr]_{s, t}
& {}
& {_0 x^{(3)}_+} \ar@{|->}[dl]^{s, t}
\\
{}
& {_{(-1)} \bot}
& {}
}
`$
使っている名前〈ラベル〉が違うので、2008年の「おとぎ話としてのn-圏 -- 計算できる図形達の世界」の名前に揃えると次のようになります。面写像〈face maps〉の名前は「バタニンの球複体 とりあえず導入」と同じ d, c にします。
$`\quad \xymatrix@C+1pc{
{}
& {\Gamma} \ar@{|->}[dl]_d \ar@{|->}[dr]^c
& {}
\\
{\alpha} \ar@{|->}[d]_d \ar@{|->}[drr]^>>c
& {}
& {\beta} \ar@{|->}[dll]_>>d \ar@{|->}[d]^c
\\
{f} \ar@{|->}[d]_d \ar@{|->}[drr]^>>c
& {}
& {g} \ar@{|->}[dll]_>>d \ar@{|->}[d]^c
\\
{A} \ar@{|->}[dr]_{d, c}
& {}
& {B} \ar@{|->}[dl]^{d, c}
\\
{}
& {*}
& {}
}
`$
球体形状を記述する指標
「指標の話: 形状の記述と形状付き集合」において、形状を記述するための指標を導入しました。その書き方で、球体の形状を記述してみます。
まず0次元の球体は一点ですから次のように記述できます。
$`\T{signature shape }\NN{Point}\: \{\\
\:\T{cells } \{\\
\quad \NN{g0}\\
\:\}\\
\:\T{dimension }\{\\
\quad \mrm{dim}(\NN{g0}) := 0\\
\:\}\\
\}`$
形状を記述する指標〈signature for shape〉は、リーディ圏〈Reedy category〉の生成系と解釈できます。上記の指標から生成されるリーディ圏を $`{\bf G0}`$ とすると、次のような圏です。
- $`|{\bf G0}| = \{\T{g0} \}`$
- $`\mrm{Mor}({\bf G0}) = \{\id_{\T{g0}} \}`$
- $`\mrm{dim}_{\bf G0}(\T{g0}) = 0`$
- その他は明らか。
次に、1次元の球体、つまり閉区間は次のように記述できます。
$`\T{signature shape }\NN{Interval}\: \{\\
\:\T{cells } \{\\
\quad \NN{g0}, \NN{g1}\\
\:\}\\
\:\T{faces }\{\\
\quad \NN{s}, \NN{t} : \T{g1} \to \T{g0}\\
\:\}\\
\:\T{dimension }\{\\
\quad \mrm{dim}(\T{g0}) := 0\\
\quad \mrm{dim}(\T{g1}) := 1\\
\:\}\\
\}`$
上記の指標から生成されるリーディ圏を $`{\bf G1}`$ とすると、次の図のような圏です。
$`\xymatrix@C+1pc{
{\T{g1}} \ar@/^1pc/[r]^{\T{s}} \ar@/_1pc/[r]_{\T{t}}
&{\T{g0}}
}
`$
さらに、2次元の球体、つまり円板は次のように記述できます。
$`\T{signature shape }\NN{Disk}\: \{\\
\:\T{cells } \{\\
\quad \NN{g0}, \NN{g1}, \NN{g2}\\
\:\}\\
\:\T{faces }\{\\
\quad \NN{s0}, \NN{t0} : \T{g1} \to \T{g0}\\
\quad \NN{s1}, \NN{t1} : \T{g2} \to \T{g1}\\
\:\}\\
\:\T{equations }\{\\
\quad \NN{st_tt} :: \T{s1};\T{t0} = \T{t1};\T{t0} \\
\quad \NN{ts_ss} :: \T{t1};\T{s0} = \T{s1};\T{s0} \\
\:\}\\
\:\T{dimension }\{\\
\quad \mrm{dim}(\T{g0}) := 0\\
\quad \mrm{dim}(\T{g1}) := 1\\
\quad \mrm{dim}(\T{g2}) := 2\\
\:\}\\
\}`$
上記の指標から生成されるリーディ圏を $`{\bf G2}`$ とすると、次の図のような圏です。
$`\xymatrix@C+1pc{
{\T{g2}} \ar@/^1pc/[r]^{\T{s1}} \ar@/_1pc/[r]_{\T{t1}}
&{\T{g1}}\ar@/^1pc/[r]^{\T{s0}} \ar@/_1pc/[r]_{\T{t0}}
&{\T{g0}}
}\\
\quad {\T{s} = \T{t1};\T{s0} = \T{s1};\T{s0} }\\
\quad {\T{t} = \T{s1};\T{t0} = \T{t1};\T{t0} }
`$
さて次は、3次元の球体、ではなくて、一挙に任意次元の球体を記述できる指標を挙げます。
$`\T{signature shape }\NN{Globe}\: \{\\
\:\T{cells } \{\\
\quad (\NX{\T{g}_k} )_{k\in {\bf N}}\\
\:\}\\
\:\T{faces }\{\\
\quad (\NX{\T{s}_k}, \NX{\T{t}_k} : \T{g}_{k + 1} \to \T{g}_{k})_{k\in {\bf N}}\\
\:\}\\
\:\T{equations }\{\\
\quad (\NX{\T{st_tt}_k} :: \T{s}_{k+1};\T{t}_{k} = \T{t}_{k + 1};\T{t}_k)_{k\in {\bf N}} \\
\quad (\NX{\T{ts_ss}_k} :: \T{t}_{k+1};\T{s}_{k} = \T{s}_{k+1};\T{s}_{k})_{k\in {\bf N}} \\
\:\}\\
\:\T{dimension }\{\\
\quad (\mrm{dim}(\T{g}_k) := k )_{k\in {\bf N}}\\
\:\}\\
\}`$
上記の指標から生成されるリーディ圏を $`{\bf G}`$ とします。$`{\bf G}`$ は無限個の対象と無限本の射を持ちますが、指標内に書いてある等式(球体恒等式)は課せられます。
球体集合
前節の形状を記述する指標 $`\T{Globe}`$ から、リーディ圏 $`{\bf G}`$ が生成されます。このリーディ圏から集合圏への関手を球体集合〈globular set〉と呼びます。球体集合 $`X`$ は次の形です。
$`\quad X : {\bf G} \to {\bf Set} \In {\bf CAT}\\
\qquad |{\bf G}| \ni \T{g}_k \mapsto X(\T{g}_k) \in |{\bf Set}| \text{ for }k\in{\bf N}\\
\qquad \mrm{Mor}({\bf G}) \ni \T{s}_k \mapsto X(\T{s}_k) \in \mrm{Mor}({\bf Set}) \text{ for }k\in{\bf N} \\
\qquad \mrm{Mor}({\bf G}) \ni \T{t}_k \mapsto X(\T{t}_k) \in \mrm{Mor}({\bf Set}) \text{ for }k\in{\bf N}
`$
球体集合は、各次元の“組み合わせ幾何的球体”達が整合的に組織化された集まりです。定義の上では、幾何的実体としての点集合は捨ててしまっていますが、幾何的〈図形的〉イメージを持ち続けたほうが分かりやすと思います(幾何的実体を回復する手段もありますし)。
球体集合の直感的・幾何的イメージを持つために、2008年の記事「おとぎ話としてのn-圏 -- 計算できる図形達の世界」の絵を再掲します。

(-1)次元の球体 $`*`$ は便宜的ダミーで、この世にひとつだけ存在します(そう考えます)。
0次元の球体は点でした。何個か(無限個かも知れない)の点が集まった集合を $`X_0`$ と書きます。点達の集合 $`X_0`$ は、関手の値として次のように書けます。
$`\quad X_0 := X(\T{g0}) \; \in |{\bf Set}|`$
同様に、1次元の球体である閉区間が何本か(無限本かも知れない)集まった集合は $`X_1`$ です。
$`\quad X_1 := X(\T{g1}) \; \in |{\bf Set}|`$
各次元の球体達の集合のあいだには面写像がありました。
$`\quad X(\T{s}_0), X(\T{t}_0) : X_1 \to X_0 \In {\bf Set}
`$
記法を簡潔にするために次のように略記しましょう。
$`\quad \T{s}_0^X, \T{t}_0^X : X_1 \to X_0 \In {\bf Set}
`$
さらに、混乱の心配がないなら、下付きの次元インデックスは省略します。上付きの $`X`$ まで省略することも多いですが、ここでは $`X`$ は付けておきます。
$`\quad \T{s}^X, \T{t}^X : X_1 \to X_0 \In {\bf Set}
`$
以上の記法の約束のもとで、次の定義をします。
$`\text{For }A, B\in X_0\\
\quad X_1(A, B) := \{ x \in X_1 \mid s^X(x) = A \;\land\; t^X(x) = B\}
`$
上の絵の「n = 1」のところに描いてあるのは $`X_1(A, B)`$ です。点〈0次元球体〉の集合 $`X_0`$ から2点 $`A, B`$ を選んで、その2点を両端とする区間〈1次元の球体〉の集まり〈束〉を描いています。
次元が上がっても同じ記法の約束を適用するとして、次の集合を定義します。
$`\text{For }f, g\in X_1(A, B)\\
\quad X_2(f, g) := \{ x \in X_2 \mid s^X(x) = f \;\land\; t^X(x) = g\}
`$
上の絵の「n = 2」のところに描いてあるのは $`X_2(f, g)`$ です。区間〈1次元球体〉の集合 $`X_1(A, B)`$ から2本 $`f, g`$ を選んで、その2本を両端とする円板〈2次元の球体〉の集まりを描いています。ただし、向き付きの円板は二重矢印で象徴的に描いています。
さらに、次の集合を定義します。
$`\text{For }\alpha, \beta\in X_2(f, g)\\
\quad X_3(\alpha, \beta) := \{ x \in X_3 \mid s^X(x) = \alpha \;\land\; t^X(x) = \beta \}
`$
上の絵の「n = 3」のところに描いてあるのは $`X_3(\alpha, \beta)`$ です。円板〈2次元球体〉の集合 $`X_2(f, g)`$ から2枚 $`\alpha, \beta`$ を選んで、その2枚を両端とする球体〈3次元の球体〉の集まりを描いています。ただし、向き付きの球体は三重矢印で象徴的に描いています。しかも、$`\Gamma`$ と名付けられた1個の球体しか描いてません。
球体集合 $`X`$ において、集合 $`X_k`$ の要素をn次元のセル〈cell of dimension n〉、あるいは短くn-セル〈n-cell〉とも呼びます。球体集合の場合は、n-セルはもちろんn次元球体です。
さて、次元が高いほうからセルの所属関係を見ていきましょう。
$`\quad \Gamma \in X_3(\alpha, \beta)\\
\quad \alpha, \beta \in X_2(f, g)\\
\quad f, g \in X_1(A, B)\\
\quad A, B \in X_0
`$
上記の情報を、「指標の話: ペースティング図とバタニン・ツリー」で述べたプロファイルパスで書くと次のようになります。
$`\quad \Gamma ::: \alpha \Rrightarrow \beta :: f \twoto g : A \to B \In X \\
\quad \alpha, \beta :: f \twoto g : A \to B \In X \\
\quad f, g : A \to B \In X \\
\quad A, B \In X
`$
これは全体として単一の3-セル〈3次元球体〉の組み合わせ構造を表すので、バタニン・ツリーで描くと、枝分かれがないツリーになります。
$`\quad \xymatrix{
{\Gamma\, \bullet} \ar@{.}[r]
\ar@{-}[d]_{\alpha}^{\beta}
&{3}
\\
{\bullet}\ar@{.}[r]
\ar@{-}[d]_{f}^{g}
&{2}
\\
{\bullet}\ar@{.}[r]
\ar@{-}[d]_{A}^{B}
&{1}
\\
{\bullet}\ar@{.}[r]
&{0}
}`$
3次元までの状況を見ましたが、もっと高い次元のセル〈球体〉があってもかまいません。球体集合が、高次圏の土台となるべき構造であることは、この例からも察することができるでしょう。
球体集合達の圏
球体集合とは、形状指標〈signature for shape〉 $`\T{Globe}`$ から定義されたリーディ圏 $`{\bf G}`$ から集合圏への関手でした。言い方を換えると、球体集合は関手圏 $`[{\bf G}, {\bf Set}]`$ の対象です。集合圏が余域となる共変関手は余前層〈copresheaf〉と呼びます。したがって、球体集合とは圏 $`{\bf G}`$ 上の余前層です。
「指標の話: 形状の記述と形状付き集合 // 形状付き集合」と同様に、スピヴァック〈David I. Spivak〉にならって、圏 $`\cat{C}`$ 上の余前層を$`\cat{C}`$-集合と呼び、$`\cat{C}`$-集合の圏を $`\H{\cat{C}}{\bf Set}`$ と書きます。この記法の約束に従うと、球体集合の圏は次のようです。
$`\quad \H{{\bf G}}{\bf Set} \;\in |{\bf CAT}|`$
球体集合を $`X, Y`$、球体集合のあいだの射を $`f`$ と書くと、射 $`f`$ は自然変換なので、次の自然性可換四角形があります。
$`\forall k \in {\bf N}.\\
\quad \xymatrix{
{X_{k+1}} \ar[r]^{f_{k+1}} \ar[d]_{\T{s}^X_k}
& {Y_{k+1}} \ar[d]^{\T{s}^Y_k}
\\
{X_k} \ar[r]_{f_{k}}
& {Y_k}
}\\
\quad \text{commutative }\In {\bf Set}\\
\quad \xymatrix{
{X_{k+1}} \ar[r]^{f_{k+1}} \ar[d]_{\T{t}^X_k}
& {Y_{k+1}} \ar[d]^{\T{t}^Y_k}
\\
{X_k} \ar[r]_{f_{k}}
& {Y_k}
}\\
\quad \text{commutative }\In {\bf Set}
`$
これは、写像の集まりである $`f`$ が、球体集合の組み合わせ幾何的構造を保つことです。
有限な球体集合達の圏
$`{\bf FinSet}`$ を有限集合達(と写像達)の圏とします。$`{\bf G}`$ 上の余前層〈共変関手〉が値をとる圏として、$`{\bf Set}`$ の代わりに $`{\bf FinSet}`$ を採用しましょう。すると、各次元のセル達が有限個である球体集合達の圏を関手圏として構成できます。
$`\quad [{\bf G}, {\bf FinSet}] \;\in |{\bf CAT}|`$
スピヴァック流の書き方なら $`\H{{\bf G}}{\bf FinSet}`$ ですね。
圏 $`\H{{\bf G}}{\bf FinSet}`$ の対象である球体集合は、次元ごとのセルは有限個でも全体としては無限個のセルを持つかもしれません。例えば、各次元の球体は1個だけど、どの次元にも球体〈セル〉があるような球体集合は、全体として無限個の球体〈セル〉を持ちます。バタニン・ツリーで描けば、地面から天空に向かって伸びる一本の紐のようなツリー(というかバンブー)になります。
球体集合 $`X`$ に対して、(集合圏内で)次の定義をします。
$`\quad \o{X} := \sum_{k\in {\bf N}}X_k \In {\bf Set}`$
$`\o{X}`$ が有限集合となる球体集合を有限な球体集合〈finite globular set〉と呼びます。有限な球体集合からなる圏は次のように書きます。
$`\quad {\bf Fin}\H{{\bf G}}{\bf Set}\;\in |{\bf CAT}|`$
次のような、圏の包含関係が成立します。
$`\quad {\bf Fin}\H{{\bf G}}{\bf Set} \subseteq \H{{\bf G}}{\bf FinSet} \In {\bf CAT}`$
今回特に話題にする圏は $`{\bf Fin}\H{{\bf G}}{\bf Set}`$ です。この圏の対象である球体集合 $`X`$ は、各次元のセルが有限個なだけではなくて、次が成立する必要があります。
$`\quad \exists m \in {\bf N}.\forall k\in {\bf N}.\, m \lt k \Imp X_k = \emptyset`$
無交差な球体集合
先に述べたように、球体集合の定義では、幾何的実体としての点集合は出てきません。面写像〈face map〉達で表現される組み合わせ構造だけが抽出されています。そのため、ちょっと奇妙なことも起きます。例えば、次の質問を考えてみてください。
- 線分(1次元球体)でもあり円板(2次元球体)でもある図形は存在するか?
答はNoですよね。しかし、球体集合 $`X`$ の定義に次のような条件は入っていません。
- $`X_1 \cap X_2 \ne \emptyset`$
例えば、1個の2次元球体とその境界達を表す球体集合として、次のような $`X`$ をとってもかまいません。
$`\quad X_k := \emptyset \:\text{ if }k \gt 2\\
\quad X_2 := \{1\} \\
\quad X_1 := \{1, 2\} \\
\quad X_0 := \{1, 2\}
`$
球体集合の次元ごとのセルの集合に共通部分〈交差〉がないとき、その球体集合は無交差〈disjoint〉だということにします。無交差は次の条件を満たすことです。
$`\quad \forall j, k\in {\bf N}. j\ne k \Imp X_j\cap X_k = \emptyset`$
$`X`$ が無交差でないとしても、次のようにして作った $`Y`$ は無交差になります。
$`\text{For }k \in {\bf N}\\
\quad Y_k := \{k\} \times X_k
`$
面写像達〈face maps〉もほんの少し変更して新しい無交差球体集合 $`Y`$ が作れます。そして、$`X`$ と $`Y`$ は同型な球体集合となります。
このことから、無交差な球体集合だけを考えても差し支えないことになります。もう少し正確な言い方をすると、無交差な球体集合達だけからなる $`\H{{\bf G}}{\bf Set}`$ の充満部分圏は、$`\H{{\bf G}}{\bf Set}`$ と圏同値となります。圏同値な2つの圏は事実上同じ圏なので、無交差な球体集合達の充満部分圏を相手にしてもいいわけです。
$`{\bf Fin}\H{{\bf G}}{\bf Set}`$ を考える際も、無交差な有限球体集合達の充満部分圏を考えれば十分です。無交差な球体集合 $`X`$ では、次が成立します。
$`\quad \o{X} = \sum_{k\in {\bf N}}X_k \cong \bigcup_{k \in {\bf N}}X_k \In {\bf Set}`$
無交差な有限球体集合 $`X`$ なら、十分大きな自然数 $`m`$ に対して次のように定義しても大丈夫です。
$`\quad \o{X} := X_0 \cup \cdots \cup X_m \cong \sum_{k\in {\bf N}}X_k \In {\bf Set}`$
直和の代わりに合併で済んでしまうのはけっこう便利なので、今後、もっぱら無交差な球体集合で考えることにします。無交差有限な球体集合の圏は次のように書きます。
$`\quad {\bf DisjFin}\H{{\bf G}}{\bf Set} \; \in |{\bf CAT}|`$
続きの記事: