「自然数の区間をAlloyで書いてみる」より:
「ある目的」とは、エイトクイーン問題を解くことです。
エイトクイーンは、「ある条件を満たすパターンを検索して列挙する」タイプの問題のなかでも典型的なモノです。Alloyにやらせるにはウッテツケの例題でしょう。
内容:
- エイトクイーン問題を解いた結果
- 問題の分析と定式化
- Eightの定義
- エイトクイーン問題の定義
- 解の検索
- 結果のエクスポートと加工
- 結果の表示
- Alloyサーバーが欲しい
エイトクイーン問題を解いた結果
次は、Alloyアナライザーが見つけてきたエイトクイーン問題の解のひとつです。
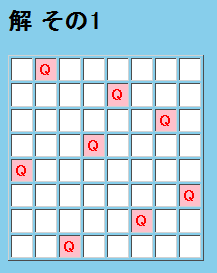
縦・横・斜め、どの方向の直線上にも、2つのクイーン(「Q」と書いてある)がいないような配置になっています。エイトクイーン問題の解はたくさんあります。他の解(5つだけですが)は、http://www.chimaira.org/tools/alloy-8queens.html に貼り付けてあります。
問題の分析と定式化
Eight = {1, 2, 3, 4, 5, 6, 7, 8} とします。8人のクイーンに、1から8の番号をふります。つまり、次のように定義します。
- Queens := Eight
クイーン達を配置する盤は8×8マスなので、Eight×Eight = {(1, 1), (1, 2), ..., (8, 8)} と考えられます。
- Board := Eight×Eight
盤を、x座標もy座標も整数である点(格子点)と考えます。q∈Queens に対して、f(q)∈Board である写像 f:Queens→Borad がクイーン達の配置に対応します。p≠q ならば、(f(p) のx座標)≠(f(q) のx座標) でなくてはならないので、クイーンの番号と盤上のx座標を一致させておきましょう。そうすれば、x∈Eight に対するy座標 h(x)∈Eight が決まれば配置が決まることになります。
x∈Eight に対する h(x) を、x番目のクイーンの高さと呼ぶことにします。h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8) に関して、「縦・横・斜め、どの方向の直線上にも、2つのクイーンがいない」という条件を書き下し、その例(モデルインスタンス)をAlloyアナライザーに検索させればいいでしょう。
Eightの定義
前節の説明では Eight = {1, 2, 3, 4, 5, 6, 7, 8} としましたが、Eight = {0, 1, 2, 3, 4, 5, 6, 7} のほうが取り扱いが少し便利なので0からはじめます。しかし、Alloyの整数は使わずに(今回の目的には組み込み整数はふさわしくない)自然数区間を自分で定義することにします。orderingライブラリを使えば線形順序を入れられますが、練習問題では車輪の再発明もアリですから、全部自前でやってみます。
Eight = {0, 1, 2, 3, 4, 5, 6, 7} のような自然数区間の性質を定義したのが「自然数の区間をAlloyで書いてみる」のintervalモジュールです。少し手直したしたので再掲します。区間の要素数は、必ずしも8じゃなくてもいいです。
-- 自然数の区間 {0, 1, 2, ..., n}
module interval
sig Interv {
-- 後者
next: lone Interv,
-- 順序
private gt : set Interv,
private ge : set Interv,
-- 距離
private delta0: Interv ->one Interv,
delta: Interv ->one Interv
}
-- ゼロと最後の数
-- この定義により、ゼロと最後の数は異なることになる。
one sig zero, last extends Interv {}
-- nextに関する公理
fact next {
{
-- lastのnextは存在しない
no last.next
-- last以外ではnextが一意に定義されている
all x: (Interv - last) |
one x.next
-- ゼロからの可達性
zero.*next = Interv
}
}
-- gt, geに関する公理(定義)
fact order {
{
gt = ^next
ge = ^next + Interv<:iden
}
}
-- delta0に関する公理
fact delta0 {
-- x < y ならば、定義されている範囲内で δ0(x, y.next) = δ0(x, y).next
all x, y: Interv |
{
x.delta0[x] = zero
y in x.*next implies
(x.delta0[y.next] in (x.delta[y]).next)
}
}
-- deltaに関する公理
fact delta {
all x, y: Interv |
-- x ≦ y ならば、δ = δ0
y in x.*next implies (delta = delta0)
-- それ以外では、δ(x, y) = δ(y, x)
else x.delta[y] = y.delta0[x]
}
/* 確認用のアサーション */
-- 距離ゼロな2点は等しいこと
assert dist_zero {
all x, y: Interv |
x.delta[y] = zero => x = y
}
-- 距離に関する不等式
assert dist_ineq {
all x, y, z: Interv |
y in gt[x] and z in gt[y]
=>
{
x.delta[z] in (x.delta[y]).gt
x.delta[z] in (y.delta[z]).gt
}
}
check dist_zero for 4
check dist_ineq for 4
エイトクイーン問題の定義
横(水平方向)に二人のクイーンが揃わない、対角線方向にも二人のクイーンが揃わないことを条件として書き下します。このとき、intervalモジュールで定義したdelta関数(関数とみなせる関係)を使います。
-- nクイーン
module queens
open interval
/* interval/delta をプライベートにして
* 絵から消したいのだけど、
* できないの?
*/
-- 盤上のクイーン達の配置を、クイーンの高さ(鉛直方向座標値)で表現する
one sig Queens {
height : Interv ->one Interv
}
-- 複数のクイーンが同じ水平線上にいない
fact horiz_safe {
all x, y: Interv |
x != y => Queens.height[x] != Queens.height[y]
}
-- 複数のクイーンが同じ対角線上にいない
fact diag_safe {
all x, y: Interv |
x != y
=>
x.delta[y] != (Queens.height[x]).delta[Queens.height[y]]
}
pred show {}
pred eight {
#Interv = 8
}
/* コマンド */
run show for 4
run eight for 8
解の検索
Alloyアナライザーで、run eight for 8 というコマンドを実行します。すると、アナライザーはエイトクイーン問題の解を探し当てます。しかし、Alloyビジュアラザーで解を表示してもナンダカわかりません。
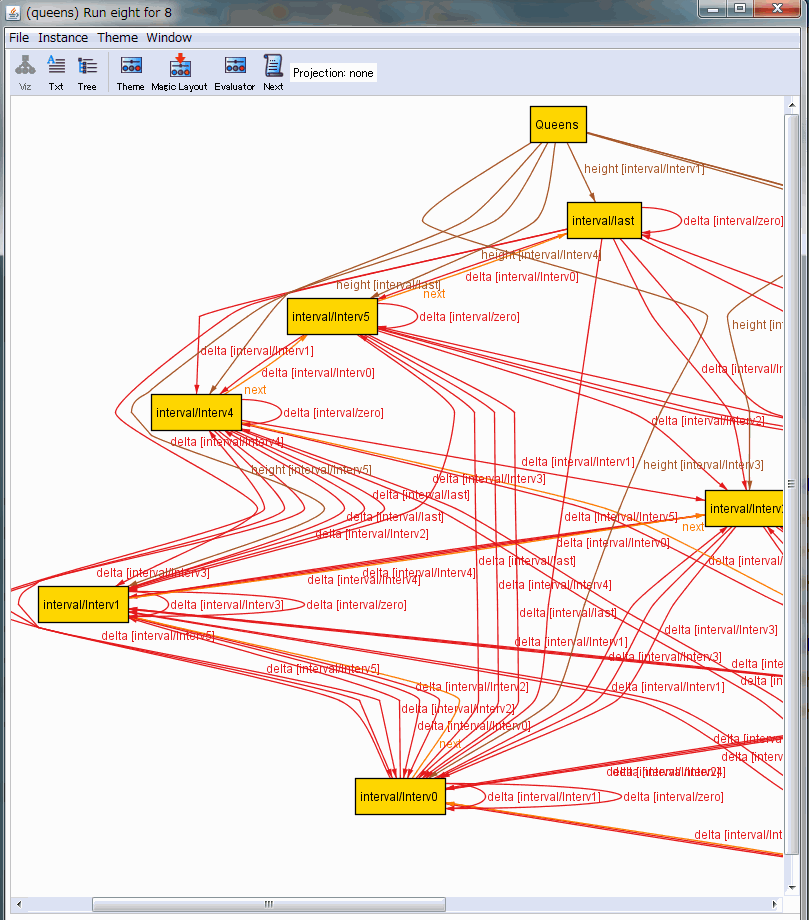
線がグチャグチャしているせいでもなくて、線をスッキリさせてもナンダカわかりません。
Nextボタンを押すと別解を次々に出しますが、次々にナンダカわからない絵が出てきます。
結果のエクスポートと加工
Alloy 4.2 Release Candidateのビジュアラザーでは、[File]-[Export To]-[XML]により、アナライザーの探した検索結果(モデルインスタンス)をXMLファイルとして書き出せます。この機能を使って、エイトクイーン問題の解をファイルにします。
エイトクイーン問題の解の本質は、[4, 0, 7, 3, 1, 6, 2, 5] のような長さ8の整数値リストに過ぎません。XMLファイルからこのようなデータを抜き出しましょう。Pythonとlxmlライブラリを使うことにしました。XPathも使えますしね。以下のコードは quick and dirty なシロモノですが、コメント(doc-string)だけは足しておきました。
# -*- coding: utf-8 -*- # # queens to HTML-table from lxml import etree _DEBUG = False; def debug_print(message): if _DEBUG: print "** " + message ZERO = 'interval/zero$0' def make_next_map(tree): """ nクイーンのAlloy出力のXML element tree 形式から next関係を記述した辞書を作成 next_map(この関数の戻り値)は、 Alloyアトムのラベルをキーとして、nextアトムのラベルを値とする。 """ next = tree.xpath('/alloy/instance/field[@label="next"]/tuple') next_map = {} i = 0 while i < len(next): next_map[next[i][0].get('label')] = next[i][1].get('label') i += 1 return next_map def next_map_to_list(next_map): """ make_next_mapの出力である辞書から Atomラベルのリストを返す。 この関数の戻りは、next関係が規定する全順序により Atomラベルを並べたリストである。 """ list = [] key = ZERO while key: list.append(key) key = next_map.get(key) return list def make_height_map(tree): """ nクイーンのAlloy出力のXML element tree 形式から height関係を記述した辞書を作成 height_map(この関数の戻り値)は、 Alloyアトムのラベルをキーとして、height値アトムのラベルを値とする。 """ height = tree.xpath('/alloy/instance/field[@label="height"]/tuple') height_map = {} i = 0 while i < len(height): height_map[height[i][1].get('label')] = height[i][2].get('label') i += 1 return height_map def make_height_list(next_list, height_map): """ make_next_listとmake_height_mapの出力をもとに ラベルを整数に直し、かつ、 インデックスアクセスが関数を表現するようなリストを返す。 """ list = [] i = 0 while i < len(next_list): key = next_list[i] height = height_map[key] list.append(next_list.index(height)) i += 1 return list class Queens(object): """ nクイーン問題の解を保持するオブジェクト """ def __init__(self, list): self.list = list def exists(self, i, j): """ n×nのマトリックスの (i, j)座標にクイーンがいるかどうか """ val = self.list[i] return val == j def toHtmlTable(self): """ クイーンの配置をHTMLテーブルとしてプリントする。 """ n = len(self.list) print '<table class="queens" border="1">' j = 0 while j < n: print '<tr>', i = 0 while i < n: if self.exists(i, j): print '<td class="q">Q</td>', else: print '<td> </td>', i += 1 print '</tr>' j += 1 print '</table>' from optparse import OptionParser import sys def main(): usage = u"""usage: %prog [options] xml_file""" version = "%prog 0.1.0" parser = OptionParser(usage=usage, version=version) parser.add_option("-d", "--debug", action="store_true", dest="debug", help="print debug message") (options, args) = parser.parse_args() if len(args) < 1: parser.print_help() exit(0) global _DEBUG _DEBUG = options.debug xml_file = args[0] try: tree = etree.parse(xml_file) except: print>>sys.stderr, ("Error: can not parse %s" % xml_file) exit(1) next_map = make_next_map(tree) debug_print("next_map = " + str(next_map)) list = next_map_to_list(next_map) debug_print("list = " + str(list)) height_map = make_height_map(tree) debug_print("height_map = " + str(height_map)) result = make_height_list(list, height_map) debug_print("result = " + str(result)) queens = Queens(result) queens.toHtmlTable() if __name__ == "__main__": main()
結果の表示
python q2table.py queens.xml とすると、次のようなHTMLテーブルを吐き出します。
<table class="queens" border="1"> <tr> <td> </td> <td class="q">Q</td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> </tr> <tr> <td> </td> <td> </td> <td> </td> <td> </td> <td class="q">Q</td> <td> </td> <td> </td> <td> </td> </tr> <tr> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td class="q">Q</td> <td> </td> </tr> <tr> <td> </td> <td> </td> <td> </td> <td class="q">Q</td> <td> </td> <td> </td> <td> </td> <td> </td> </tr> <tr> <td class="q">Q</td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> </tr> <tr> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td class="q">Q</td> </tr> <tr> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> <td class="q">Q</td> <td> </td> <td> </td> </tr> <tr> <td> </td> <td> </td> <td class="q">Q</td> <td> </td> <td> </td> <td> </td> <td> </td> <td> </td> </tr> </table>
例えば、次のようなスタイルを付けると、チェス盤に見えなくもないです。
<style> body { background-color: skyblue; } td { width: 18px; height: 18px; text-align: center; background-color: white; } td.q { color: red; background-color: pink; font-weight: bold; } </style>
2番目の解なら:

Alloyサーバーが欲しい
エイトクイーン問題の解はたくさんありますが、http://www.chimaira.org/tools/alloy-8queens.html には6つの解しか載せていません。6つでやめちゃった理由は、ビジュアラザーの[Next]ボタンを押して、[File]-[Export To]-[XML]でダイアログを開いてファイル名を入力して、… のような作業がやんなっちゃったからです。
スクリプト言語からAlloyエンジンにアクセスできるなら、全部の解を取り出して長いHTMLファイルを作るのも自動的にやれるんですがね。
JavaのAPIを使う方法がありますが、それだとJavaプログラムを書く必要があります。ソケットでもパイプでもHTTP通信でもなんでもいいので、Alloyエンジンとやり取りする口を開いて待っているサーバーがあるといいのですが。今のGUIとは別なインターフェースでAlloyエンジンを利用できたらより面白いと思うんですよね。