このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

関手的データモデル入門 2：統一的に制約を書く方法

雑記／備忘

夢のような話も楽しいけど、今日は地道に行きましょう。様々なスキーマ制約を、単純な発想だけを使って、すべて一様に扱う方法を紹介します。


それにしても、「入門 2」なんて番号付けていいんでしょうかね？ 「衝撃的なデータベース理論・関手的データモデル 入門」を「入門 1」とみなすつもりですが、「入門 3」「入門 4」があるかどうか不安。

内容：

  1. データたちのいるところ
  2. 集合と部分写像
  3. 従業員と事業所の例
  4. 主キーと外部キー
  5. 従属性（冗長性）
  6. ビジネスルール
  7. スキーマにおける制約記述法のまとめ

データたちのいるところ

関手的データモデルは、データベース理論を極限まで単純化します。基本概念は、テーブル、カラム、制約の3つだけです。この3つだけであらゆることを記述しようとします。背後に、対象、射、可換図式だけであらゆることを記述する圏論があるので大丈夫、ってことです。

そうはいっても現実は複雑です。複雑性を簡潔に記述できる道具が欲しくなることもあります。そのような道具を得るひとつの方法は、データが棲む世界に構造を入れることです。スピヴァックのオリジナルの定式化では、データベーススキーマS上のデータベース状態（データベースインスタンスとも言う）は、関手 D:S→Set です。Setは集合と写像の圏ですが、集合圏が潜在的に持っている豊かな構造は何も使ってません（少なくともオリジナルの定式化では）。

集合圏Setは、直積や部分対象の分類などの構造を持っているので、それを使えば複雑なことができます*1。圏Setを、別な圏に切り替える方法もあります。僕は、Setより部分写像の圏Partial（後述）が使いやすいと思っているので、ここではデータの棲家はPartialであるとして話をします。Partialを採用するメリットは「関手的データモデルをどう説明するか？ 考えてます」の「アンビエント圏は部分写像の圏がよいだろう」に書いてあります。

（画像は、http://yaplog.jp/mukiguri/archive/98 の http://img.yaplog.jp/img/16/pc/m/u/k/mukiguri/0/452.jpg を拝借しました。）

集合と部分写像

AとBを集合として、Aの部分集合X上で定義された写像は、AからBへの部分写像と呼びます。Xがなんであっても「Aから」である点に注意してください。これから先考える“写像”はすべて部分写像です。データベースの文脈で言えば、undefinedの意味のNULLを認めることになります。

fがAからBへの部分写像であるとき、定義域であるXを Def(f) と書くことにします。Def(f)⊆A であり、fをDef(f)の上に制限すれば普通の意味の写像となります。ちなみに圏論では、Aのことを「定義域」と呼ぶことはありません。単に域（domain）です*2。

undefinedの意味のNULLを記号「⊥」で表すことにして、次の3つは同じ意味だとします。

  • fはxにおいて未定義である
  • f(x) = ⊥
  • xはDef(f)に所属してない

もちろん、次の3つも同じ意味です。

  • fはxにおいて定義されている
  • f(x) ≠ ⊥
  • xはDef(f)に所属しいる（x∈Def(f)）

どんなfに対しても、f(⊥) = ⊥ と考えると、部分写像を普通の写像のように扱えます*3。

以下では、f:A→B と書いたら、fは部分写像だとします。Def(f) = A であれば、fをA上の普通の写像と考えることができます。f:A→B が Def(f) = A のとき、fは全域（total または entire）であるといいます。部分写像が全域のとき、それは普通の写像となります。普通の写像は部分写像の特別な場合ですが、fが普通の写像であると主張するときは「fは全域」という条件を付けます。

集合と部分写像からなる体系をPartial（常に太字）と書きます。Partialはもちろん圏になります。Partialが圏であることの詳細は割愛しますが、次の言葉使い／記号法だけは押さえておいてください。

  1. 集合を、Partialの対象と呼ぶ。
  2. 部分写像を、Partialの射と呼ぶ。
  3. 射（部分写像）f:A→B と g:B→C のこの順の結合（合成）を、f;g と書く。f;g:A→C となる。
  4. 対象（集合）Aに対して、idA:A→A は恒等写像のことだとする。

従業員と事業所の例

サンプルとして、会社の情報を蓄えるデータベースを考えます。Employeeを従業員のテーブル、Officeを事業所のテーブルとします。スキーマ記述は「衝撃的なデータベース理論・関手的データモデル 入門」と同じ書き方を使うことにします。「//」はコメントです。



table Employee {

  // 勤務している事業所

  office: Office,
  // ...

};
table Office {

  // 事業所の住所（所在地）

  addr: String,
  // 事業所の責任者

  chief: Employee,
  // ...

};

データ型Stringもテーブルとして扱うのでした（fixed table String {}; と宣言される）。この3つのテーブルと、スキーマに明示的に書かれている（省略されてない）カラムだけを絵に描くと次のようです。

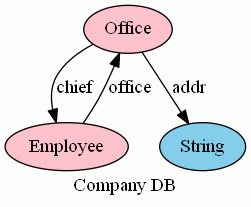
色の区別は： 水色は時間的に変化しないテーブル（データ型）、ピンクは時間に沿って変化するテーブルです。

この例を使って、次のようなことを、関手的データモデルの言葉で説明してみます。

  • 主キーと外部キー
  • 従属性（冗長性）
  • ビジネスルール

主キーと外部キー

関手的データモデルでは、テーブルのあいだの射（ここでは部分写像）をカラムと呼ぶのでした。次のカラムがあります。

  1. office:Employee→Office
  2. addr:Office→String
  3. chief:Office→Employee

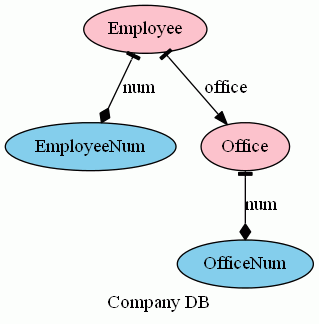
現実的な都合を考えると、従業員番号、事業所番号により従業員と事業所を識別すると便利です。番号なので、その値はIntegerとすればいいのですが、整数を用途により区別して、EmpoyeeNum、OfficeNum という2つのデータ型（テーブル）を導入します。番号のカラムはnumという名前にします。テーブル名とドットによる修飾で同名カラムを区別しましょう。

  • Employee.num:Employee→EmployeeNum
  • Office.num:Office→OfficeNum

これらを加えて再度絵を描くと：

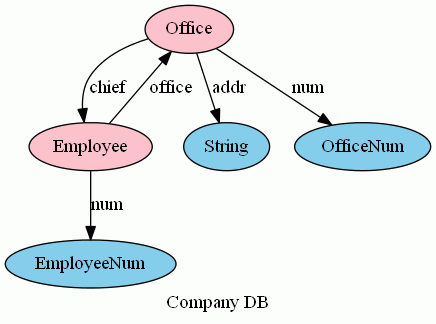
Employee.num と Office.num は次の条件を満たす必要があります。

  1. 全域である。
  2. 単射的である。

fが単射的（injective）とは、「x≠y、f(x)≠⊥、f(y)≠⊥ ならば f(x)≠f(y)」のことです。上の2条件を別な言い方で書くと：

  1. すべてのレコードに番号が振ってある。
  2. 異なるレコードには異なる番号が振ってある。

さらに、データベースでお馴染みの言い方にするなら：

  • Employee.num と Office.num は主キーである（主キーに選んだ）

となります。つまり、主キー制約とは、「主キーに選んだカラムが全域単射的」という主張と同じです。

さて、office:Employee→Office と chief:Office→Employee に対して、番号を使った代理のカラム officeNum:Employee→OfficeNum、chiefNum:Office→EmployeeNum を考えてみます。officeNum, chiefNum を点線で描き加えたのが図の次です。

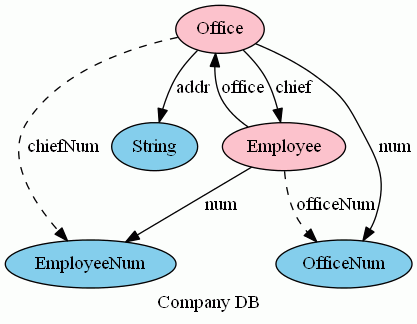
officeNum, chiefNum が、きちんとoffice, chiefの代理をしていることを表す等式は次のようになります。

  • officeNum = office;Office.num : Employee→OfficeNum
  • chiefNum = chief;Employee.num : Office→EmployeeNum

この代理のカラムである条件が、外部キー制約です。コンピュータでデータを扱うときは、番号は便利なので、代理の技法がしばしば使われるわけです。しかし、所詮「代理は代理」であることをお忘れなく。

従属性（冗長性）

従業員レコードから、その従業員の勤務先（事業所）の住所を取り出すカラムがあったとします。

  • officeAddr:Employee→String

このようなカラムは次の条件を満たすはずです。

  • officeAddr = office;addr : Employee→String

絵で描けば：

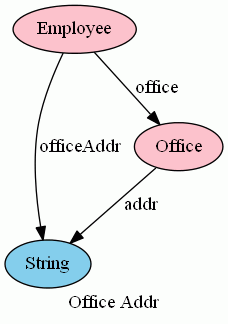
この図式では、office, addr, officeAddr が作る三角形が“可換”です。図式が可換とは、図式上のどの経路（パス）をたどっても結果が同じことです。

officeAddrは、officeの値から求まるので、officeAddrはofficeに従属していると言われます。従属性を表す等式 officeAddr = office;addr は、officeAddrというカラムを office;addr という他の2つのカラムの結合（composition）で定義すればいいことを示します。最初からofficeAddrを入れる必要がないのでこのカラムは冗長だと言われたりもします。

圏論のアンダー圏（余スライス圏、余カンマ圏）をご存知の方に向けての説明： スキーマSのアンダー圏 Employee/S において、office→officeAddr という射が存在することが従属性なので、「従属性＝アンダー圏の射」です。

「衝撃的なデータベース理論・関手的データモデル 入門」に出した例の計算カラムageも同様な話で、次の図のようになっています。

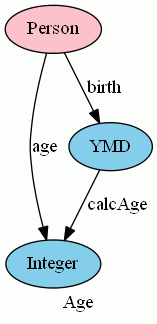
これも可換な図式です。等式で書けば次のとおり：

  • age = birth;calcAge : Person→Integer

ビジネスルール

いまサンプルとして話題にしている会社では、事業所には必ず責任者（chief）がいて、責任者は当該の事業所に勤務する必要があるとします。これは、会社の取り決めですからビジネスルールと言っていいでしょう。このビジネスルールは次のように記述できます。

  • chief:Office→Employee は全域である。
  • chief;office = idOffice : Office→Office

Officeを図の上では2個にコピーして描くと次のようになります。

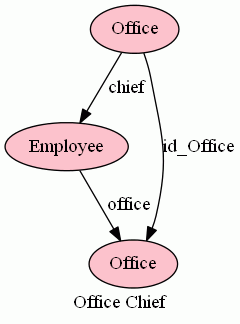
これまた可換図式です。

スキーマにおける制約記述法のまとめ

関手的データモデルでは、スキーマは有向グラフで可視化できます。頂点（ノード、バーテックス）をテーブル、辺（エッジ、アーク）をカラムと呼ぶのでした。スキーマを構成する第三の素材が制約です。

今までの例から、制約は次のような基本的な制約の組み合わせだと分かります。

  1. カラムが全域（total, entire）であるという制約
  2. カラムが単射的（injective）であるという制約
  3. 「カラム1 = カラム2」という形の等式制約

最後の等式は「パス1 = パス2」と書いたほうが分かりやすいかもしれません。しかし、「f:A→B と g:B→C がカラムなら、その結合（composition） f;g:A→C もカラム」なので、パスとカラムを区別する必要はありません。

等式制約は可換図式によって視覚化されます。有向グラフに含まれる三角形や四角形に対して「これは可換」とマーク付けすることです。全域性や単射性を視覚化するには、矢印の形や色を変える方法が使われます。例えば次の図では、全域なら矢印の根本に棒、単射的なら矢印の先をダイアモンドにしてみました。

この図では、従業員の勤務先は常に確定しています（これも制約のひとつ）。しかし、従業員の配属が未定の状態を認めるなら、officeの矢印の根本にある棒は取り除きます。

全域性／単射性の可視化の約束は、いま僕が、GraphVizの矢印レパートリーからテキトーに選んだものです。なにかしら約束を決めて合意すれば済む話です（広く合意された標準があるのが望ましいですが）。こういう印は、なかなか覚えられないので、「(全域)」とかテキストで注釈を入れたほうがいい気もします。

ところで、全域性／単射性も可換図式で定義できないか？ というと、圏論的に定義される演算（オペレーター）を使えばできます。さらに、等式より高い表現力を持つ不等式を使うこともできます。不等式を使うときは可換図式の概念も拡張します*4。

拡張をしても、テーブル（頂点）、カラム（辺）、制約（三角形、四角形などの多角形）が基本になる事情は変わりません。このような単純化は、むしろ豊かさにつながります。関手的データモデルは、データベース理論を極限まで単純化することにより豊かな実りをもたらすのです。

*1:Setはトポスなので、トポスの構造まで使えば、ほとんど何でも出来てしまいます。

*2:ドメインという言葉は多義的です。関係モデルでは原子的な値の領域らしいですし、プログラム意味論（領域理論）のドメインもありますし。

*3:Maybeモナド（付点モナド）のクライスリ圏を作っていることになります。

*4:可換図式を、可逆とは限らない2-セルに拡張します。