スピヴァックの関手データモデルでは、圏の表示が重要な役割を果たします。なにもスピヴァック理論にかぎらず、圏一般において表示は重要です。特に有限表示(finite presentation)は、我々人間が手で圏を書き下す唯一の方法と言っていいでしょう。そこで、圏の有限表示について考えてみます。
圏の有限表示とは、“ノードの個数”も“辺の本数”も有限な有向グラフと、有限個のパス同値関係(path equivalence relations)の組です。パス同値関係とはスピヴァックの用語で、普通に言えば可換図式です。
圏の有限表示を絵、つまり実際の有向グラフで描けば視覚的に把握できていいのですが、いつでも絵を描くのは面倒です。テキストによる表現を考えます。方針は次のとおり。
- キーボードのタイピング量を減らす。
- 見た目が割と自然になるように。
次の記事で書いたことが背景になっています。
内容:
対象と射の記述
圏は対象と射からなるので、それらを愚直に列挙すれば圏を記述できます。例えば:
- 対象: A, B, C
- 射: f:A→B, g:B→C, h:A→C
これは圏全体を書き尽くしてはいませんが、恒等射や結合(composition)で作られる射は自動的に追加されるとみなします。この圏の名前をFooとして、絵に描くと次のようになります。
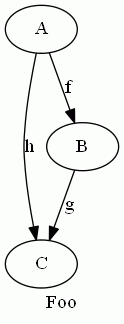
この絵を描くためのGraphViz DOT言語のソースは次のようになります。
digraph Foo {
graph [label=Foo];
A;
B;
C;
A -> B [label=f];
B -> C [label=g];
A -> C [label=h];
}
CafeOBJで書くなら次のようでしょう。
module Foo {
[A B C]
op f : A -> B
op g : B -> C
op h : A -> C
}
「タイピング量を減らす」方針から、射の両端に登場する対象の宣言は省略していいとします。対象が孤立ノードになるときは明示的に書く必要があります。CafeOBJのopのようなキーワードはなしにして、単に射(と孤立した対象)をカンマ区切りで並べるだけにしましょう*1。
category Foo {
f: A -> B,
g: B -> C,
h: A -> C
}
対象の名前と射の名前は同じ名前空間に入れます。したがって、対象と射に同じ名前を付けることはできません。その代わり、対象の名前は、対応する恒等射の名前としても使えるとします。このルールだと、A: A -> A は意味を持ちます。
孤立した対象を持つ例を挙げておくと:
category Bar {
u: A -> X,
v: X -> B,
g: B -> B,
C,
Y
}
CとYは孤立してます。
パス同値関係の記述
射の結合には、図式順結合の標準的記号である「;」を使います。fとgの結合は、f;g です。f;g のような結合をグラフ上のパスとみなし、2つのパスを等号で結んだ等式がパス同値関係です。例えば、f;g = h 。パス同値関係は、whereというキーワードで区切った後にカンマ区切りで並べることにします。
category Foo {
f: A -> B,
g: B -> C,
h: A -> C
where f;g = h
}
CafeOBJなら、変数を持つ論理式を使います。
module Foo {
[A B C]
op f : A -> B
op g : B -> C
op h : A -> C
var x : A
eq g(f(x)) = h(x) .
}
論理式の部分は、∀x∈A.(g(f(x)) = h(x)) のことです。パス同値関係では変数は不要です。そもそも、圏の射が写像とは限らないので、限量子や束縛変数を用いた論理式は使えません。
whereを使って、互いに逆になっている射からなる圏を記述してみましょう。
category Iso {
f: A -> B,
g: B -> A
where
f;g = A,
g;f = B
}
余代数風、代数風の記述
同じ域(domain)を持つ複数の射をまとめて書く記法を導入しましょう。A -> {f:B, g:C} と書くと、f: A -> B, g:A ->C の略記とします。同様に、{f:A, g:B} -> C は f: A -> C, g: B -> C の略記です。
この記法は単なる略記に過ぎませんが、射の集まりを余代数風または代数風にグルーピングできます。「前後に進める場所(位置)の集合」を意図した圏の例を挙げます。数字(この例では1)も名前に使えるとします。
category Movable {
start: 1 -> S,
true: 1 -> Boolean,
S -> {next: S, prev: S, isStart: Boolean}
where
start;isStart = true,
next;prev = S,
prev;next = S
}
この圏Movableをスキーマとみなしてのインスタンスを集合圏Setで作るとリング状になります。直線状の列にするには、部分写像の圏Partialをアンビエント圏に使って、イコール以外の関係も入れる必要があります。
「衝撃的なデータベース理論・関手的データモデル 入門」で出した次の絵もテキストで表現してみます(絵の下)。
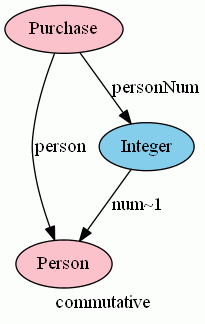
category PieceOfBookPurchase {
Purchase -> {personNum: Integer, person: Person},
num~1: Integer -> Person
where
person = personNum;num~1
}
関手の記述
関手は、2つの表示のあいだの次のような写像で表現できます。
- 対象(グラフのノード)には、対象を対応させる。
- 射(グラフの辺)には、パスを対応させる。
- パス同値関係は保存される。
対応を示す記号は矢印「->」でもいいのですが、一文字節約して「>」にします。対象Aが対象Xに対応することは A > X です。射 f がパス g;h に対応することは f > g;h と書きます。
この記法で対応を完全に列挙すれば済むのですが、かなり面倒なので、次のような約束を設けて記述の簡略化をします。
- 同じ名前の対象は、デフォルトで対応付ける。明示的に対応を記述すればオーバーライドされる。
- 同じ名前の射は、デフォルトで対応付ける。明示的に対応を記述すればオーバーライドされる。
- パス同値関係の保存から必然的に導かれる(推論できる)対応は書かなくてもよい。
実例を挙げます。
category Foo {
f: A -> B,
g: B -> C,
h: A -> C
where f;g = h
}
category Bar {
u: A -> X,
v: X -> B,
g: B -> B,
C,
Y
}
functor F: Foo -> Bar {
C > B,
f > u;v
}
ちょっと苦しいですが図示すると次のようです。u;v、u;v;g とラベルされた点線矢印は結合で生成された射で、パスの意味となります。破線矢印は対象のあいだの対応です。射のあいだの対応まで描くと煩雑なので(うまく描けないし)省略してあります。関手による対応のだいたいの様子はこの図から把握できるでしょう。
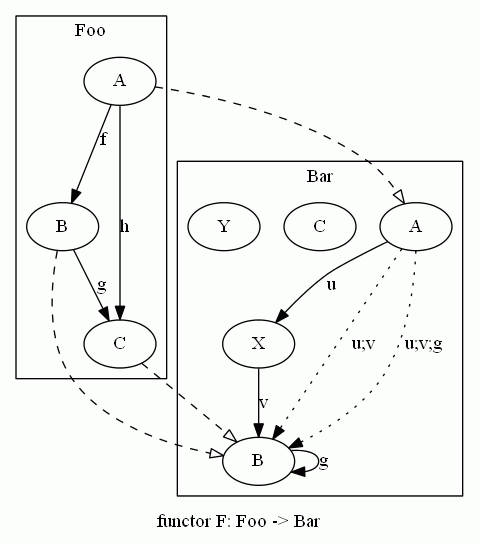
FooとBarを異なる“高さ”に描いて、破線矢印が垂直に落ちるように描けると随分と見やすくなると思います。つまり、3次元のGraphVizが欲しい!
可愛い圏をガンガン使おう
スピヴァックによると「category = schema」です。ですから、category Foo と書いたところは schema Foo でも同じです。モジュール、クラス、余クラス(代数)なんてのもスキーマであり、つまりは圏です。スピヴァックのオリジナルの定式化はプレーンな圏を使ってますが、デカルト圏や順序豊饒圏(Order-enriched category)などを使えば、計算科学/ソフトウェアのモジュール/クラスなどはたいてい、スピヴァックの意味のスキーマとして定式化できます。
このとき、スキーマとして出てくる圏にはとても小さなモノもあります。例えば、category Empty {} は空圏、category Unit {A} は単一の対象(と恒等射)だけを持つ圏です。こういう小さな小さな圏も立派な圏であり、圏論の対象物です。「小規模な圏に注目しよう」と、僕はずっと強調しています。「はじめての圏論 第9歩:基本に戻って、圏論感覚を養うハナシとか」より:
従来、圏の事例というと、集合と写像の圏、位相空間と連続写像の圏、アーベル群と加法的(線形)写像の圏などが引き合いに出されていました。これらの例を僕は個人的に“重い圏”と呼んでいます。[…省略…] 物理学やコンピューティング・サイエンスでも圏が常用されつつあるご時世に、初っぱなにこんな重い例を出すのはイカガナモンでしょうか。
「「物理系実務者のための圏論入門」への補遺+檜山の戯言」で、ボブ・クックの「物理系実務者のための圏論入門」の要旨(abstract)をイイカゲンに訳してるんですが:
この論説の目的は、物理関係者 -- 特に量子力学/量子情報学の研究者や利用者に、圏論が日々の実践に必須な道具であることを納得してもらうことである。圏論が役に立つ理由は、それがよりカッコヨク数学を行う手段であるからではない。そんなこっちゃなくて、モノイド圏が、実務上の物理システムを実際に表現する代数構造に他ならないからである。
以下は、僕の感想です。
圏論の利用法やご利益として、異なる分野の共通性を抜き出して定式化できることがあります。なんつうか、抽象的なフレームワーク(概念的枠組み)として役に立つってことです -- これ、良い意味でのアブストラクト・ナンセンス。この点に全然異論はないのだけど、別な側面として、実際(アクチュアル)に圏がそこかしこに実在している、だから圏論で調べる、ってこともあります。
ボブ・クックが言っていることは; 「アブストラクト・ナンセンスとしての圏論カコイイ」とかはどうでもよくて、物理的システムと物理的操作(物理的過程)の全体は、実際に具体的にモノイド圏なんだから、もうしょうがないだろうよ。しのごの言ってないで圏論(特にモノイド圏論)使えよ、オマイラ。
簡単で軽い圏の例は「可愛い圏」でも出しています。
具体的なスキーマとして現れる圏は可愛い圏です。可愛い圏は手で触れるデータです。加工したり組み合わせたりも手で(あるいはコンピュータで)出来ます。絵に描くことも出来ます。可愛い圏は、まだまだ活用の場がある有用な道具ですよ。スピヴァックのフレームワーク(これは重い圏)内で、可愛い圏をガンガン使いましょう。
[追記]
射のあいだの対応まで描くと煩雑なので(うまく描けないし)省略してあります。
射もノードにしてみたら、射のあいだの対応まで描いても、まー見られる感じの絵ですね。
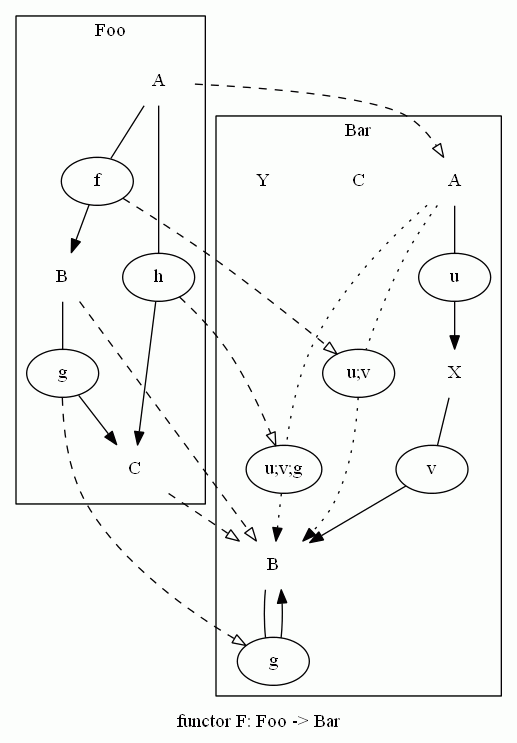 [/追記]
[/追記]