ダンジョン圏における確率伝搬法 - 檜山正幸のキマイラ飼育記 (はてなBlog)

昨日の記事「確率グラフィカルモデルの背後にある圏は何か？」の課題にドンピシャで役立ちそうな論文を見つけました。

Title: Belief propagation in monoidal categories
Author: Jason Morton
Pages: 8p
URL: https://arxiv.org/abs/1405.2618

短い論文ですが、その割に色々な話題に触れていて、図が一枚もなく、用語法が（僕から見ると）独特で読みやすくありません。でも、僕にとって役立ちそうな概念が記述されていました。特に、次の3つは興味深いです。

再配置〈reshaping〉
ダンジョン圏〈dungeon category〉
スパイダー射〈spider morphism〉

この3つの概念をザッと説明します。

内容：

再配置と再配置可能圏
ダンジョン圏とスパイダー射
おわりに

再配置と再配置可能圏

再配置〈reshaping〉はモートン論文の6ページに書いてあります。昨日の記事で書いた置換曲げ同値関係に別な定式化を与える目的で、モートンの再配置を少し拡張した（置換を入れた）形で説明します。

C = (C, $\otimes$ , I, σ) （記号の乱用、一部省略）を対称モノイド圏として、X₁, ..., X_m, X_m+1, ..., X_m+n を m+n 個のCの対象とします（重複があってもかまいません）。次のような射を考えます。

f:X₁ $\otimes$ ... $\otimes$ X_m → X_m+1 $\otimes$ ... $\otimes$ X_m+n in C

これから、f∈Mor(C) に対して別な（同じこともあるが）射 resh(f)∈Mor(C) を対応させるオペレーター（射から射への写像）を定義します。これらのオペレーターは、再配置データと呼ばれるデータRによってインデックスされているので、f $\mapsto$ resh_R(f) と書きます。resh_Rを（再配置データRから決まる）再配置オペレーター〈reshaping operator〉、または単に再配置〈reshaping〉と呼びます（まだ定義はしてないけど）。

先に直感的な意味を述べておきます。昨日の記事で出した置換曲げ同値な3つの射の絵を再掲します。

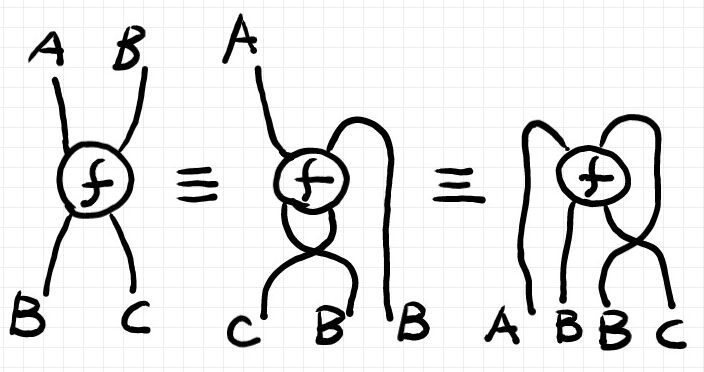
置換曲げ同値な射は、再配置オペレーターにより相互に行き来できます。別な言い方をすると、置換曲げ同値という同値関係 f ≡ g を、オペレーター〈作用素〉による変換可能性 resh_R(f) = g の形で与えることもできます。

まず、再配置データを説明します。[m+n] = {1, ..., m, m + 1, ..., m+n} という略記を使います。I, J⊆[m+n] として、I∪J = [m+n], I∩J = {} とします。つまり、IとJは[m+n]を二分割しています。I, J が空集合であることも許します（後で追加説明します）。集合Iの個数（基数）をk, 集合Jの個数をℓとします。当然に、m+n = k+ℓ です。

集合[m+n]の二分割 I, J に加えて、全単射写像 τ_I:[k] → I, τ_J:[ℓ] → J を一緒にした R = (I, J, τ_I, τ_J) を（[m+n]の）再配置データ〈reshaping data〉と呼びます。

[m+n]の再配置データ R = (I, J, τ_I, τ_J) が与えられると、[m+n] = [k+ℓ] の置換〈自己全単射写像〉σ = σ_R :[k+ℓ] → [m+n] が決まります。その決め方は：

1≦ i ≦k のとき σ(i) := τ_I(i)
k＜ i ≦k+ℓ のとき σ(i) := τ_J(i-k)

さて、最初に挙げたCの射 f:X₁ $\otimes$ ... $\otimes$ X_m → X_m+1 $\otimes$ ... $\otimes$ X_m+n in C と、[m+n]の再配置データ R = (I, J, τ_I,τ_J) に対して、g = resh_R(f) は次のプロファイルを持ちます。σ_R を単に σ と略記します。

g:X_σ(1) $\otimes$ ... $\otimes$ X_σ(k) → X_σ(k+1) $\otimes$ ... $\otimes$ X_σ(k+ℓ)

具体例を挙げましょう。X₁ = A, X₂ = B, X₃ = B, X₄ = C として、

f:X₁ $\otimes$ X₂ → X₃ $\otimes$ X₄
つまり、f:A $\otimes$ B → B $\otimes$ C

とします。

I = {1}, J = {2, 3, 4}, τ_I = (1 $\mapsto$ 1), τ_J = (1 $\mapsto$ 4, 2 $\mapsto$ 3, 3 $\mapsto$ 2) は再配置データRを定義します。この再配置データRに伴う置換は (1 $\mapsto$ 1, 2 $\mapsto$ 4, 3 $\mapsto$ 3, 4 $\mapsto$ 2) となります。よって、再配置オペレーターの結果 resh_R(f) のプロファイルは、

resh_R(f):X_σ(1) → X_σ(2) $\otimes$ X_σ(3) $\otimes$ X_σ(4)
これは、resh_R(f):X₁ → X₄ $\otimes$ X₃ $\otimes$ X₂
つまり、resh_R(f):A → C $\otimes$ B $\otimes$ B

となります。fが上の図の左側だとすれば、resh_R(f) は上の図の真ん中になります。

別な再配置データとして、R2 = ({}, {1, 2, 3, 4}, (), (1 $\mapsto$ 1, 2 $\mapsto$ 3, 3 $\mapsto$ 3, 4 $\mapsto$ 2) を取ります。[2+2] = {1, 2, 3, 4} の分割が{}と{1, 2, 3, 4}なので片方が空です。このとき、resh_R(f) の域〈domain〉をどうするか？これは空な添字に渡るモノイド積なので単位対象とします。resh_R(f) のプロファイルは次のようになります。

resh_R2(f):I → X_σ(1) $\otimes$ X_σ(3) $\otimes$ X_σ(2) $\otimes$ X_σ(4)
つまり、resh_R2(f):I → A $\otimes$ B $\otimes$ B $\otimes$ C

fが上の図の左側だとして、resh_R2(f) は上の図の右側になります。

対称モノイド圏Cにおいて、f:X₁ $\otimes$ ... $\otimes$ X_m → X_m+1 $\otimes$ ... $\otimes$ X_m+n の形のすべての射と、[m+n]の再配置データRに対して、fの再配置 resh_R(f) が定義されていて、対称との整合性があるとき、対称モノイド圏Cは再配置可能〈reshapable〉だといいます。

対称との整合性があるときは、id_A⊗B:A $\otimes$ B → A $\otimes$ B と、[2+2]の再配置データ R = ({1, 2}, {3, 4}, (1 $\mapsto$ 1, 2 $\mapsto$ 2), (1 $\mapsto$ 4, 2 $\mapsto$ 3)) に対して、次が成立することです。

resh_R(id_A⊗B) = σ_A,B

再配置可能圏を、一人前の圏の種別として定義するには、もう少し工夫や追加が必要でしょうが、再配置オペレーターという概念が使いたいだけなので、この程度でも十分でしょう。

ダンジョン圏とスパイダー射

モートン論文のタイトルである「モノイド圏における確率伝搬法」は、単なるモノイド圏ではなくてダンジョン圏において実行されるアルゴリズムです。ダンジョン圏〈dungeon category〉とは、長い名前でもいいなら「一貫性を持つ特殊可換フロベニウス代数モダリティを備えた厳密コンパクト閉対称モノイド圏」です。「コンパクト閉対称モノイド圏」は、最近は単に「コンパクト圏」と呼ぶので、もう少し短くできます。

ダンジョン圏と同じ概念を、フォング〈Brendan Fong〉とスピヴァック〈David Spivak〉はハイパーグラフ圏〈hypergraph category〉と呼んでいるようです。

https://ncatlab.org/nlab/show/hypergraph+category

モートンは、ダンジョン圏を定義するのに先立って、スパイダー付き圏〈spidered category〉を定義していますが、中間にスパイダー付き圏を設けることは不要な気がします。必要なのは、「特殊可換フロベニウス代数モダリティを備えた厳密コンパクト圏」におけるスパイダー射の概念です。

スパイダー射〈spider morphism〉とは、次の射を基本〈原子的射〉として、結合とモノイド積で組み立てられる射のことです。[追記]モノイド圏の構造射である結合律子〈associator〉、左単位律子〈left unitor〉、右単位律子〈right unitor〉も入りますね。モートンは厳密モノイド圏（一般のモノイド圏を厳密化した後）を想定していたような気がします。[/追記]

恒等
対称
フロベニウス代数の乗法
フロベニウス代数の単位
フロベニウス代数の余乗法
フロベニウス代数の余単位
コンパクト構造の単位
コンパクト構造の余単位

Cが「特殊可換フロベニウス代数モダリティを備えた厳密コンパクト圏」のとき、Cのスパイダー射の全体は部分圏になるので、その部分圏を Spid(C) と書きます。Cが一貫性〈coherence〉を持つとは、部分圏 Spid(C) がやせた圏になることです。

スパイダー射の概念が必要なのは、因子グラフ（昨日の記事参照）の解釈のためです。変数ノードをスパイダー射、関数ノード〈因子ノード〉をスパイダーとは限らない射と解釈するのです。なるほどね。

因子グラフと、黒丸で描いた頂点〈ドット〉を含めたストリング図は同じものですから、ストリング図で考えてもかまいません。上の箇条書きで列挙した射は黒丸で描く約束になり、黒丸とワイヤーだけで構成されるストリング図に対応する射がスパイダー射となります。

ダンジョン圏は再配置可能な圏になります。この事実は、有向ストリング図（通常のストリング図）と無向ストリング図を行き来するときに使われます。無向ストリング図に特定の向きを付けて議論しても、再配置オペレーターを施しても議論が変わらないなら、向き付に依存しない議論になります。

おわりに

モートンによれば、ダンジョン圏〈ハイパーグラフ圏〉では確率伝搬法が働くようです。このことから、ダンジョン圏は良い性質を持つ圏だと言えるでしょう。一方で、確率的議論をする一般的な枠組みとしてマルコフ圏があります。一般論としてのマルコフ圏と特論としてのダンジョン圏、あるいはその中間に位置する圏達のあいだの関係を、ストリング図ベースで考えると、確率的現象のグラフィカルな記述が何であるか？を理解する助けになりそうです。