以前、「letrecとwhere」という記事を書きました。この頃僕は、letとletrecという二つのキーワードは要らないのじゃないのか、と思っていました。最近、「スンマセンデシタ、二つ要ります」と反省しています。
let = letrec としたかったのは、letrecが6文字もあるので書くのがめんどくさい、というショーモナイ理由です。3文字のletをletrecの意味で使えば、短く書けていいな、っと。
3文字のletをletrecの意味に使うと、本来のletは使えなくなります。でもwhereで代用できます。つまり、次のように使い分ければいいかな、と。
- 前置のlet -- 実はletrecの意味で、再帰を考慮する。
- 後置のwhere -- 再帰を考慮しない単純な置き換え。
しかし、「letrecとwhere」に書いたように、letとwhereのペアが構文としてバランスが悪いなー、とも思ったりしました。バランスの悪い構文で、前置と後置を使い分け、whereは5文字だし、… と、そんなにいいことないじゃん。3文字余分にキーボードを叩くことを我慢して、前置のletとletrecに統一したほうが幸せみたい。
どうでもいい話を書いているので、ちょっと理屈の補足をします。f:X→X に対する不動点は、ミュー記号を使って μx.t のように書きます。ここでtは、関数fを表現する項(term)で、変数xは、変域Xを走ると想定しています。項tに自由変数aが含まれるなら、f:A×X→X のように考えて、μx.t はAでパラメータ付けされた不動点族 A→X を表すと考えます。
letrecは、μx.t を使いやすくした形で、g:X→Y という後続する関数を一緒にして、g(μx.t) を letrec x = t in s と書くのです。sは関数gを表す項です。sも自由変数を持っていてもかまいません。tとsの自由変数を一緒にしたパラメータ領域を改めてAと書くと、letrec x = t in s は、g(μx.t) の別表記であり、A→Y という関数を表現します。
X = X1× ... ×Xn、A = A1× ... ×Am ならば、fを成分表示して、
f(x1, ..., xn, a1, ..., xm)
= (
f1(x1, ..., xn, a1, ..., xm),
...
...
...
fn(x1, ..., xn, a1, ..., xm)
)
のように書けます。成分fi に対応する項をtiとすれば、g(μx.t) は、letrec x1 = t1 ... xn = tn in s となるわけです。letrecが再帰を表現できるのは、関数の再帰的な定義が高階関数の不動点を求めることであり、ミューオペレータが不動点を求めるオペレータだからです。
一方、letは再帰や不動点とは無関係で、let x1 = t1 ... xn = tn in s は、関数合成 g(f) に対応する項を作るだけです。letはパラメータ(自由変数)を持てたり、部分的な束縛を書けたりするので、単なる関数合成(=射の結合)よりは柔軟ですけど。
「6文字もあって長い」なんてブータレたんですが、letrecはホントに良く出来たシンタックスシュガーだなー、と感心します。letやwhereとも組み合わせて書くと、人間にとって比較的に自然で、それでいて厳密な記述ができます。素晴らしいですね。
[追記]
letrecの話は去年(2013年)の夏にもしてますね。僕の好みの話題。
letrecといえば、まさに「不動点方程式とトレース付き圏」を具現している構文なんですが、そこらへんのことは、長谷川真人さんの素晴らしいスライドで見事に解説されています。
長谷川さんのスライドの絵は「これはひどい誤解だ -- フローチャートは手続き型…だってぇー?!」でも引用しています。
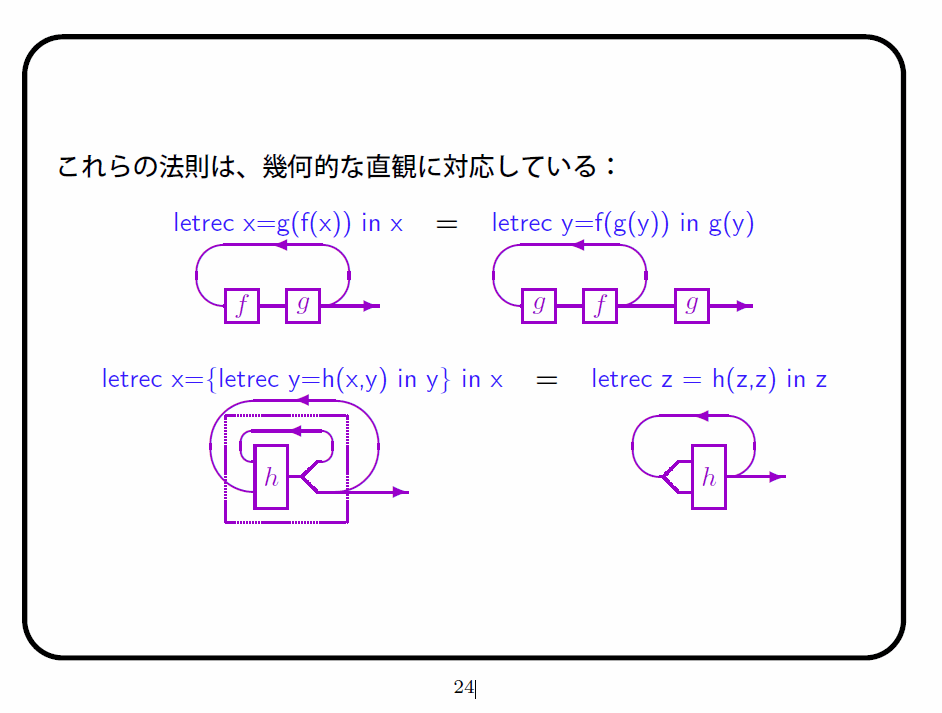
上のほうの letrec x = g(f(x)) in x = letrec y = f(g(y)) in g(y) という等式は、先日話題にした対角自然性(dinaturality)です。9月30日の記事で出しておいた等式 (f#g)† = (g#f)†#g が、letrec でちゃんと表現できます。
下側の letrec x = {letrec y = h(x, y) in y} in x = letrec z = h(z, z) in z は、ダブルダガー公式とか対角性とか呼ばれているものです。これも不動点の大事な性質(形式的には公理として扱う)です。
「フローチャートをめぐる迷信と妄言と愚昧」でも次の絵を引用しているのでした。
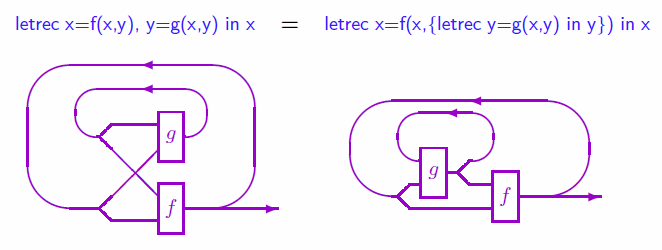
式の右側が切れてしまっていますが、等式は letrec x = f(x, y), y = g(x, y) in x = letrec x = f(x, {letrec y = g(x, y) in y}) in x となります。これは、連立不動点方程式が、ガウスの消去法で解けることを主張しているもので、ベキッチ(Beki'c)の公式と呼ばれたりします。成分の方程式を順番に解いていけば連立方程式が解ける、という実にありがたい公式です。
[/追記]