随伴のニョロニョロ関係をTypeScriptで確認する - 檜山正幸のキマイラ飼育記 (はてなBlog)

遅ればせながら、明けましておめでとうございます。年は変われど、僕の興味はあいも変わらず。

Cがデカルト閉圏のとき、直積による掛け算関手と関数空間を作る指数関手*1は随伴ペアとなります。この事実が型付きラムダ計算のモデル作成のベースとなります。つまり、C(X×A, Y) $\stackrel{\sim}{=}$ C(X, Y^A) が成立して、この同型がカリー化／反カリー化を与えるわけです。逆に、型付きラムダ計算が行えるプログラミング言語のなかには随伴ペアとカリー同型がなんらかの形で備わってます。

ところで、随伴性はニョロニョロ関係式によっても定義できます。型付きラムダ計算が行えるプログラミング言語では、掛け算関手と指数関手に関するニョロニョロ関係式が成立しているはずです。このニョロニョロ関係式を、当のプログラミング言語のなかで確認することができるでしょうか？ TypeScriptで試してみました。

内容：

掛け算・指数、随伴、ニョロニョロの復習
ニョロニョロ確認作戦
確認方法とソースコード
人類が犯した過ちについて

掛け算・指数、随伴、ニョロニョロの復習

Cをデカルト閉圏として、その対象A∈|C|をひとつ選んで固定します。X |→ X×A で定義される関手をP_Aとします。PはproductのPです。関手P_Aを、対象部（object part）と射部（morphism part）に分けて書けば：

P_A(X) := X×A
P_A(f:X→Y) := λ(x, a)∈X×A.(f(x), a)

次に、X |→ X^A で定義される関手をE_Aとします。EはExponential objectのEです。指数対象X^Aは、A→X という形の射達がなす関数空間だと解釈できます。実際には、射そのものではなくて、射をコード化したモノ達が再び対象となっていて、それをX^Aと書くのです。コード化／デコード化がカリー同型です。関手E_Aも、対象部と射部に分けて書けば：

E_A(X) := X^A
E_A(f:X→Y) := λe∈X^A.λa∈A.f(e(a))

この辺のことは、次の記事が参考になるかも知れません。

以下、対象Aは固定して変更しないので、下付きのAを省略して、掛け算関手と指数関手を単にP、Eと書きます。

PとEは随伴ペアで、PはEの右随伴、EはPの左随伴となります。このことは、どんなCの対象X, Yに対しても、次のカリー同型が成立することでした。

C(P(X), Y) $\stackrel{\sim}{=}$ C(X, E(Y))

随伴性の別な表現がニョロニョロ関係式（snake relation）です。絵で描けば簡単で、曲がったワイヤーを伸ばせるよ、という主張です。

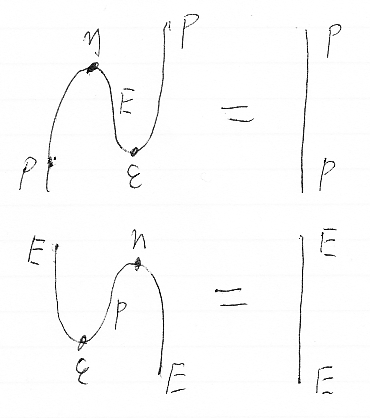
ηとεは自然変換で、それぞれ随伴の単位と余単位と呼ばれます。絵と相性が良いDOTN二号記法なら、目で見たまんまにテキスト等式を書き下せます。

(η*P);(P*ε) = P
(E*η);(ε*E) = E

絵の描き方やニョロニョロについては次の記事に説明があります。

通常の反図式順記法（anti-diagrammatic-order notation）では、並びの順番を逆にしたり、下付き添字と丸括弧と結合（合成）の記号を組み合わせたりと煩雑になります。だけどしょうがないので、通常記法でも書き下しておきます。IをCの恒等関手として、自然変換ηとεのプロファイルは：

η::I⇒EP:C→C
ε::PE⇒I:C→C

X∈|C|を取って自然変換を適用すれば：

η_X:X→EP(X) in C
ε_X:PE(X)→X in C

Xを使ってニョロニョロ関係式を書くと：

ε_P(X) $\circ$ P(η_X) = id_P(X)
E(ε_X) $\circ$ η_E(X) = id_E(X)

ハァー、デコボコが鬱陶しい。

掛け算関手Pと指数関手Eの場合の単位と余単位を具体的にラムダ式で書きましょう。指数X^Aは A->X とも書くことにします。P(X) = X×A、E(X) = A->X です。

η_X:X->(A->(X×A)) = λx∈X.λa∈A.(x, a)
ε_X:(A->X)×A->X = λ(f, a)∈(A->X)×A.f(a)

余単位εは、(f, a) |→ f(a) なので、evalまたはapplyのことです。

ニョロニョロ確認作戦

ニョロニョロ関係式をもう一度見てみましょう。

ε_P(X) $\circ$ P(η_X) = id_P(X)
E(ε_X) $\circ$ η_E(X) = id_E(X)

2つの等式は対称的な形をしてますが、実際に具体的に調べる立場では対称（同等）ではありません。それぞれの等号を考える舞台は、

equality on C(P(X), P(X))
equality on C(E(X), E(X))

です。P(X) = X×A なので、一番目の等式は「データのペアを引数とする関数の等しさ」です。一方、E(X) = A->X なので、二番目の等式は「関数を引数として関数を値とする関数の等しさ」となります。「関数の等しさ」がそもそも確認できない事なのですが、関数を引数として関数を値とする関数（高階関数）の等しさとなると、数個の具体例での確認さえできません。なので二番目のニョロニョロ関係式の確認は諦めます。

一番目のニョロニョロ関係式なら、数個のペアデータを両辺の関数に渡して、結果が等しいなら「成立していそうだ」という気分になれます。ほんとの確認は数個のペアデータではダメで、すべてのペアデータを調べないといけません。たいていは不可能なので、これも諦めます。

値の計算だけではなくて記号の計算（項の変形）も出来るシステムなら、ニョロニョロ等式の証明もできるでしょうが、TypeScriptでは無理です。気分で満足しましょう。

TypeScriptの型パラメータの使い方などの基本事項は次を参照。

TypeScriptと関手やモナドなど

TypeScriptで関手を表すには、関手の対象部として型構成子、射部として総称関数を使います。型構成子は型パラメータ付きのクラスを使いました。そのため、ちょっと冗長なところがあります。直積X×Aは、X型のプロパティ（フィールド、メンバー）fstとA型のプロパティsndを持つオブジェクトです。指数 X^A = A->X は、TypeScript関数型 (a:A)=>X のプロパティfunを持つオブジェクトにしています。自然変換は、型パラメータを持つ型のあいだの総称関数です。

対象Aは固定するのですが、Aとしてstringを選びました。A = string です。

assertNyoroNyoro<X> という関数が、次の等式に相当します。

ε_P(X) $\circ$ P(η_X) = id_P(X)

x∈X と s∈string である引数を持つので、次のように書くとより実状に近いです。

λ(x, s)∈X×string. ( (ε_P(X) $\circ$ P(η_X))(x, s) = id_P(X)(x, s) )

型パラメータXをnumberに具体化したものが、assertNyoroNyoroNumber関数で、これは型パラメータを持たない具体的関数です。もっとも、JavaScriptにコンパイルしてしまうと、assertNyoroNyoro<X> と assertNyoroNyoroNumber は同じですけどね。

確認方法とソースコード

nyoronyoro.tsをtscでコンパイルしてnyoronyoro.jsを作り、次のようなHTMLファイルを作ってブラウザ・コンソールで確認できます。

<html>
  <head>
    <title>nyoronyoro</title>
    <script src="nyoronyoro.js"></script>
  </head>
  <body>
    <h1>nyoronyoro</h1>
  </body>
</html>



> assertNyoroNyoroNumber(0, "hello")

  0 == 0 && "hello" == "hello"

  true

> assertNyoroNyoroNumber(1, "明けましておめでとうございます。")

  1 == 1 && "明けましておめでとうございます。" == "明けましておめでとうございます。"

  true

>

nyoronyoro.tsはこの記事の最後に貼り付けてあります。

人類が犯した過ちについて

毎度思うことなんだけど、ほとんどの人が反図式順記法を使っているのって間違っているよ。僕は、ε_P(X) $\circ$ P(η_X) = id_P(X) なんてデコボコグチャグチャした等式は見ただけでゲロ吐きそうなんだけど、コミュニケーションのためには通常記法で書かざるを得ないから書いているんです。

絵を描いて「なるほど」と思えるまではさしたる手間じゃないときでも、それから通常テキスト記法に翻訳するのが大変。プログラミング言語の構文も、右から左への順で、適用と合成と型パラメータは違う書き方をしているので、反図式順記法と同じ。こんなに分かりにくくて手間がかかる記法を標準に採用していることは人類が犯した過ちであり悲劇だと思うのだが。苦労しているのは僕だけかい？

ソースコード（nyoronyoro.ts）

// nyoronyoro.ts

// stringによる積（掛け算） X |→ X×string
class Prod<X> {
    fst: X;
    snd: string;

    constructor (x:X, s:string) {
	this.fst = x;
	this.snd = s;
    }
}
// 射に対する積（掛け算） f |→ f×string
// Prod_fmap<X, Y>: (f:(x:X)=>Y) => ((p:Prod<X>)=>Prod<Y>)
function Prod_fmap<X, Y>(f:(x:X)=>Y) : (p:Prod<X>)=>Prod<Y> {
    return (
	function (p:Prod<X>) {
	    return new Prod<Y>(f(p.fst), p.snd)
	}
    );
}


// stringによる指数 X |→ X^string
class Exp<X> {
    fun: (s:string)=>X;

    constructor (f:(s:string)=>X) {
	this.fun = f;
    }
}
// 射に対する指数 f |→ f^string
// Exp_fmap<X, Y>: (f:(x:X)=>Y) => ((e:Exp<X>)=>Exp<Y>)
function Exp_fmap<X, Y>(f:(x:X)=>Y) : (e:Exp<X>)=>Exp<Y> {
    return (
	function (e:Exp<X>) {
	    return new Exp<Y>((s:string) => f(e.fun(s)));
	}
    );
}

// 随伴の単位 η<X>: Id<X> → Exp<Prod<X>>
// eta<X>: (x:X) =>  Exp<Prod<X>>
function eta<X> (x:X) : Exp<Prod<X>> {
    var fun: (s:string)=>Prod<X>;
    fun = (s:string) => new Prod<X>(x, s);
    return new Exp<Prod<X>>(fun);
}

// 随伴の余単位 ε<X>: Prod<Exp<X>> → Id<X>
// epsilon<X>: (fx:Prod<Exp<X>>) => X
function epsilon<X>(fx:Prod<Exp<X>>) : X {
    var fun: (s:string)=>X;
    fun = fx.fst.fun;
    var arg: string = fx.snd;
    return fun(arg);
}


// ニョロニョロの左辺上部
//
//   eta<X>: (x:X)=>Exp<Prod<X>>
//   Prod_fmap<X, Y>: (f:(x:X)=>Y) => ((p:Prod<X>)=>Prod<Y>)
//   ----------
//   Prod_fmap<X, Exp<Prod<X>>(eta<X>): (p:Prod<X>) => Prod<Exp<Prod<X>>>
//
// Prod_eta<X>: (p:Prod<X>) => Prod<Exp<Prod<X>>>
function Prod_eta<X>(p:Prod<X>) : Prod<Exp<Prod<X>>> {
    return (
	Prod_fmap<X, Exp<Prod<X>>>(
	    (x:X)=>eta<X>(x) // eta<X> を生で入れると構文エラーになってしまう
	) (p)
    );
}

// ニョロニョロの左辺下部
//
//   Exp_fmap<X, Y>: (f:(x:X)=>Y) => ((e:Exp<X>)=>Exp<Y>)
//   epsilon<X>: (x:X) =>  Exp<Prod<X>>
//   ----------
//   epsilon<Prod<X>>: (hf:Prod<Exp<Prod<X>>>) => Prod<X>
//
// 関数定義はしない。

    
// ニョロニョロの左辺
// Z<X>: (p:Prod<X>) => Prod<X>
function Z<X>(p:Prod<X>) : Prod<X> {
    return (
	epsilon<Prod<X>>(Prod_eta<X>(p))
    );
}

// ニョロニョロの右辺
// id_Prod<X>: (p:Prod<X>) => Prod<X>
function id_Prod<X>(p:Prod<X>) : Prod<X> {
    return p;
}

// ニョロニョロ関係のアサーション
// 注意：型Xは、== による等値判定が可能でなくてはならない。
function assertNyoroNyoro<X>(x:X, s:string) : boolean {
    // 引数
    var p:Prod<X> = new Prod<X>(x, s);
    // 左辺
    var lhs:Prod<X> = Z<X>(p);
    // 右辺
    var rhs:Prod<X> = id_Prod<X>(p)
    // アサーション
    if (lhs.fst == rhs.fst && lhs.snd == rhs.snd) {
	console.log(lhs.fst + " == " + rhs.fst + " && " +
		    '"' + lhs.snd + '" == "' + rhs.snd + '"');
	return true;
    } else {
	console.log(lhs.fst + " != " + rhs.fst + " || " +
		    '"' + lhs.snd + '" != "' + rhs.snd + '"');		    
	return false;
    }
}

// アサーションの具体化： X = number とする。
// numberは、== による等値判定が可能である。
function assertNyoroNyoroNumber(x:number, s:string) : boolean {
    return assertNyoroNyoro<number>(x, s);
}

*1:[追記]指数関手という言葉は曖昧ですね。X, Y |→ Y^X というニ変項関手か、Aを固定しての X |→ A^X か、それとも Y |→ Y^A か分からないです。Y |→ Y^A は、Aによる累乗関手、A-乗関手と呼ぶのがいいかも。[/追記]