昨日書いた記事「確率的圏における期待値と雑音」で、記法の選び方をしくじりました。
- Sの射を、'F', 'G' と書いた。
- 文字'G'の使用が衝突した。
絵のなかで'G'を使っていたので修正しませんでした（絵の描き直しが面倒）。他にも、ベースの圏Mとクライスリ圏Sがゴッチャになっていて分かりにくいかと思います。僕は一度書いた記事は書き直さない（単なるモノグサです）ので、昨日の記事はそのままですが、今後のために注意事項を書いておきます。単に記法の話だけではなくて、周辺の概念（表題参照）も説明します。
内容：
クライスリ圏の使いみち
Cを圏として、Cの自己関手 T:C → C と自然変換 μ::T＊T ⇒ T:C → C, η::IdC ⇒ T:C → C は、モナド (T, μ, η) を形成しているとします。'＊'は関手の図式順結合記号で、Idは恒等関手を表します。いつもの記号の乱用で、T = (T, μ, η) と書きます。
Kは、モナドTのクライスリ圏だとします。
- K := Kl(C, T) （Klはクライスリ圏を作り出すオペレータ）
プログラマ・技術者にとってのモナドは、クライスリ圏を作り出す素材のようなものです。クライスリ圏Kの射は、（なんらかの意味で）拡張された関数となり、通常の関数（Cの射）だけでなく拡張された関数も使えるようになり便利だなー、となります。
一方でクライスリ圏は、次の問に答えるための仕掛けでもあります。
- モナドTを、関手の随伴対 J -| S を使って T = J＊S と分解できないか？
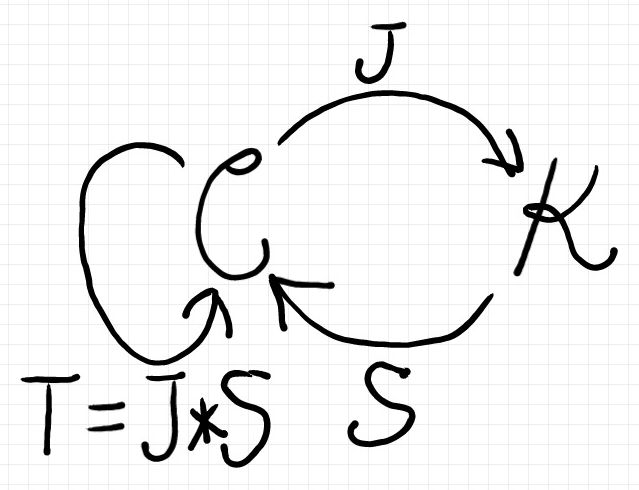
クライスリ圏Kに対して、J:C → K と S:K → C をうまく作ると、JとSは随伴対で、J＊S により T:C → C が再現します（下図）。この事実は、クライスリ圏を拡張された関数の圏として使う立場でも知っておいていいと思いますよ。なので、次節以降で説明します。
転置と反転置
「圏論の随伴をちゃんと抑えよう // 転置と反転置」の復習をしましょう。一般に、F:C → D と U:D → C が随伴関手対（Fが左、Uが右）だとします。このとき、ホムセットのあいだに次の同型（集合のあいだの双射）があるのでした。
- D(F(A), X)
C(A, U(X))
ちなみに僕は、この形に書いたとき「カンマの左に現れるFが左、カンマの右に現れるUが右」と随伴の左右を覚えています。
エミリー・リエル〈Emily Riehl〉にならい、上記の同型〈双射〉で移り合う2つの射は互いに転置〈mutually transposed〉といいます。左から右への同型写像を転置〈transposition〉D(F(A), X) → C(A, U(X))、右から左への同型写像を反転置〈opposite-transposition〉C(A, U(X)) → D(F(A), X) と呼び、(-)∩（転置）、(-)∪（反転置）という演算子記号で表します（下図）。
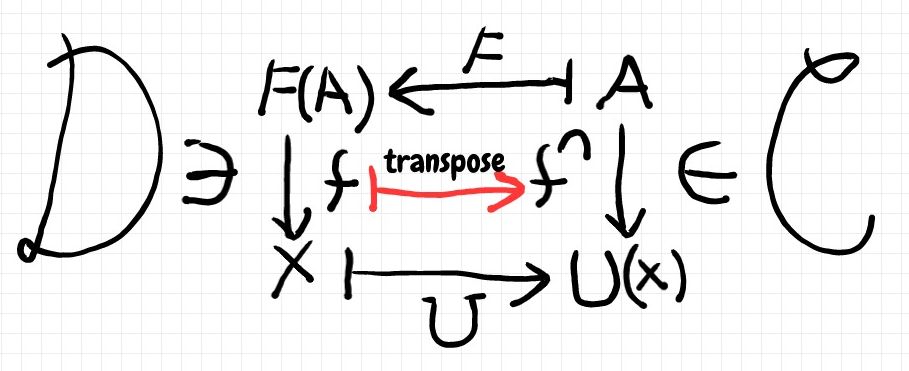
以上で一般論の復習は終わりで、Cが一般的圏、Fが随伴対の左関手という設定もオシマイです。後で出てくる C, F は別な文脈で解釈します。こう断らないと、また記号の衝突になりますからね、念の為。
さて、モナドTが載った圏Cとそのクライスリ圏Kの話に戻ります。(J:C→K) -| (S:K→C) が随伴対のとき、今説明した転置・反転置同型が次の形で存在します。
- K(J(X), Y)
クライスリ圏の場合は、この転置・反転置同型がイコールになってしまうのです。
- K(J(X), Y) = C(X, S(Y))
さらに、J(X) = X, S(Y) = T(Y) なので、
- K(X, Y) = C(X, T(Y))
転置・反転置同型がだいぶ退化した形で現れます。それが原因で、CとKがゴチャ混ぜの印象を受けます。“互いに転置な K(X, Y) の要素と C(X, T(Y)) の要素”は、実体としては同じでも役割が違います。転置記号 (-)∩ と反転置記号 (-)∪ を付けて役割を区別することにします。
- F:X → Y in K ⇔ F∩:X → T(Y) in C （ただし、実体としては F = F∩）
- f:X → T(Y) in C ⇔ f∪:X → Y in K （ただし、実体としては f = f∪）
クライスリ射は二面性を持つのだと思ってください。“クライスリ圏Kの射”としての面と、“ベースの圏Cの射”としての面です。それらの二面を、記号 '∪', '∩' を添えてトグルします。
小学校の運動会にかぶる帽子で、ひっくり返すと赤白入れ替わるのがありましたよね。先生が赤組に入ったり白組に入ったりしている情景を思い浮かべてください。同一人物である先生が、帽子をひっくり返すたびに赤組メンバー／白組メンバーと入れ替わります。記号 '∪', '∩' によるトグルとは、帽子のひっくり返しのようなものです。
「実体としては同一でも役割としては別物」という状況は頻繁に現れます。次の記事は、セミナーの補足資料として書いたものですが、この状況に慣れるために役立つかも知れません。
クライスリ結合とクライスリ恒等射
「確率的圏における期待値と雑音」が読みにくい原因のひとつは、ベースの圏の結合／恒等射とクライスリ圏の結合／恒等射を同じ記号で表していることです。圏は異なっても結合／恒等射は同じ記号で書くのは極めて普通なので、特に責められることではないのですが、クライスリ圏の文脈では分かりにくくなります。
「マルコフ核： 確率計算のモダンな体系」では、クライスリ圏の結合（チャップマン／コルモゴロフ結合）とクライスリ圏の恒等射は普通とは違う記号（反図式順）を使っていました。
| ベースの圏 | クライスリ圏 | |
|---|---|---|
| 反図式順結合 | ||
| 恒等射 |
'Id'は恒等関手に使うので変更して、以下では次のようにします（反図式順記号は今回使いませんけど）。
| ベースの圏 | クライスリ圏 | |
|---|---|---|
| 反図式順結合 | ||
| 図式順結合 | ||
| 恒等射 |
「マルコフ核： 確率計算のモダンな体系」では、射のプロファイル（域と余域）を表す矢印も変えて、F:X →* Y のような書き方をしていました。が、そこまでは面倒だなぁ、普通の矢印にします。どこまで親切な記法（めんどくさい記法）を採用するかの判断は難しいですね。
クライスリ圏と随伴性
記法の準備が出来たので、ベースの圏Cとクライスリ圏Kを結ぶ随伴関手対を構成します。クライスリ圏Kのもとになったモナドは (T, μ, η) です（念の為）。
関手 J:C → K の定義：
- X in C（X∈|C|）に対して、J(X) := X
- f:X → Y in C （f∈C(X, Y)）に対して、J(f) := (f;ηY)∪
ここで、(f;ηY)∪ は、C内で作った f;ηY:X → T(Y) in C を（同じモノですが）K内の X → Y という射とみなしたモノという意味です。'∪'を付けて役割（所属する圏）が変わったことを明示しています。
Jが関手であることは次の等式が成立することです。
- f:X → Y, g:Y → Z in C に対して、J(f;g) = J(f);;J(g) in K
- X in C に対して、J(idX) = kidJ(X) in K
クライスリ結合 ;; とクライスリ恒等射 kidX の定義は：
- F:X → Y, G:Y → Z in K に対して、F;;G := (F∩;T(G∩);μZ)∪
- X in K に対して、kidX := (ηX)∪
これらの定義を使えば、Jの関手性は明白に示せるでしょう。
次に関手 S:K → C の定義：
- X in Kに対して、S(X) := T(X)
- F:X → Y in K に対して、S(F) := (F∩)#
ここで、f# は、f:X → T(Y) in C のクライスリ拡張〈Kleisli extension〉で次のように定義されます。
- f:X → T(Y) in C に対して、f# := T(f);μY :T(X) → T(Y) in C
Sが関手であることは次の等式が成立することです。
- F:X → Y, G:Y → Z in K に対して、S(F;;G) = S(F);S(G) in C
- X in K に対して、S(kidX) = idS(X) in C
Sの関手性も定義に従えば難しくはないです。
J -| S であることを示す次の同型（転置・反転置同型）も、(F∩)∪ = F, (f∪)∩ = f の形で示せます（つうか自明）。
- K(J(X), Y)
そして、J＊S = T :C → C も容易に確認できます。最初に与えられたモナドTが、随伴関手対 J -| S に分解されたことになります。
今回の記事くらいに記号の選択を注意すれば、J -| S, J＊S = T を示すのは容易ですが、通常レベルの記号のオーバーロード（多義的使用）／乱用を使ってしまうと、なにがなんだか分かりません。いつでも記号の区別をするのは面倒でたまりませんが、必要なときはキチッと区別したほうがいいですよ。
