このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

従順な複体から作られる3次元の圏 -- toward 量子と古典の物理と幾何＠名古屋

雑記／備忘

一連の記事「* -- toward 量子と古典の物理と幾何＠名古屋」は、“話すこと”より“話さないこと”を書いていくシリーズになってきましたね。まー、それはそれでいいですけど。

単体複体（simplicial complex）に対して一般化と制限を施した図形からなる高次圏を背後で使う予定です。しかし、この高次圏を「量子と古典の物理と幾何＠名古屋」で説明する余裕はないと思うので、ここに書いておきます。「何をするのか」「何故それをするのか」「何の役に立つのか」を先に読んで、あとは斜め読み／飛ばし読みでもいいと思います。これは予備知識とかではありません、もちろん。

なお、この記事では、「圏」という言葉で高次元の圏を意味することもあるのでご注意ください。

内容：

何をするのか

これから、とある3次元の圏を構成します。この圏は具体的な圏なので、固有名詞で呼ぶことにします。圏の名前はAKB12とします。憶えやすく親しみやすいように、アイドルグループの名称に似せています。

綴り字の逆順で文字の意味を説明します。まずは概略だけです。出てくる用語の意味も説明してないので、いま伝わるのは雰囲気だけでしょう。詳細は後述します。

12は「ジュウニ」ではなくて「イチとニ」です。1次元と2次元の意味です。BはbordismのBです。bordismとcobordismという2つの言葉は双対ではなくてほぼ同義で、境界関係という意味を持ちます。どちらかというと、「コボルディズム」のほうが多く使われているかも知れません。B12で、1次元図形のあいだの2次元(コ)ボルディズムの圏ということになります。コボルディズム自体は1次元境界を持つ2次元の図形です。

Kはcomplicialに由来し、complicialはcomplexからの形容詞です。えっ、KじゃなくてCだろう？と。ドイツ語ならkomplexです、とか言ってみる。扱う図形が、単体複体（simplicial complex）を少し一般化した複体なので、形容詞complicial（強引にkomplicial）を付けておきます。

AはamenableのAです。すべての複体を考えると厄介すぎるので、扱いやすい複体だけに限定します。その扱いやすい複体を従順複体（amenable complex）と呼ぶことにして、従順複体だけで構成される圏を考えます。後で述べるように、従順複体は、一点複体、折れ線複体、ビーズ複体のどれかです。

3次元の圏AKB12は、従順複体の従順コスパン（amenable cosopan）から構成されます。AKB12の3-射（3-セル）を表すペースティング図（ストリング図ではない！）は次のような形です（ゴチャゴチャで汚いけど）。

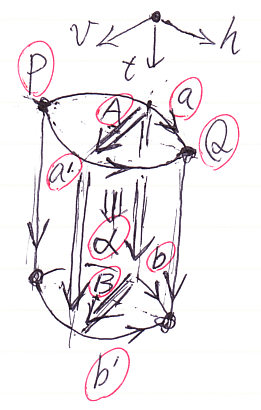
これは、2-射Aから2-射Bへ向かう3-射 α:::A≡>B の絵です。αに関連して、次の射（セル）が描かれています。

  1. 対象（0-射）P, Q, R, S
  2. h1-射 a:P→Q, a':P→Q, b:R→S, b':R→S
  3. hv2-射 A::a⇒a', B::b⇒b'
  4. t1-射（無名） P→R, Q→S
  5. ht2-射（無名） a⇒b, a'⇒b'
  6. 3-射 α:::A≡>B

3-射には、これら6種類の射が付随します。略記号の意味は次のとおり：

  1. h = horizontal （水平、横）
  2. v = vertical （垂直、縦）
  3. t = transversal （横断的）

水平方向、垂直方向、横断的方向の3つの方向があります。横断的方向は、時間方向を表すときもあります（応用に依存する）。なお、射の種類と次元に関しては「高次圏の次元について -- toward 量子と古典の物理と幾何＠名古屋」も参照してください。

上の図は円柱のような形に描いてますが、これは方体（キューブ）が退化したものだとみなすとよいでしょう。方体状の3-射を描くと次のようです。ただし、煩雑になるので2次元の射（矢印⇒）は明示してません。


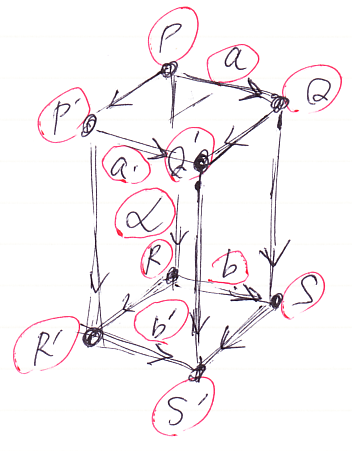
  1. 対象（0-射）P, Q, P', Q', R, S, R', S'
  2. h1-射 a:P→Q, a':P'→Q', b:R→S, b':R'→S'
  3. v1-射（無名） P→P', Q→Q', R→R', S→S'
  4. hv2-射 A::a⇒a', B::b⇒b'
  5. t1-射（無名） P→R, Q→S, P'→R', Q'→S'
  6. ht2-射（無名） a⇒b, a'⇒b'
  7. vt2-射（無名） (P→P')⇒(R→R'), (Q→Q')⇒(S→S')
  8. 3-射 α:::A≡>B

このような方体（キューブ）状の3-射を持つ3次元の圏に関しては、次が参考になります。

何故それをするのか

何故、AKB12を構成するのでしょうか。実は、我々はAKB12自体に興味があるわけではありません。AKB12は道具に過ぎないのです。実際に扱うものは、幾何由来のある種の代数系です。これを仮称Hとしましょう。Hは直感的に理解しやすいものですが、その定義があまりハッキリせず代数的な構造もぎごちないのです。要するに、Hは中途半端でモヤッとした存在です。

Hの定義とその性質をハッキリさせるために、well-definedな圏Kを作って、HをKに埋め込みます。HをKの部分系として理解しよう、ということです。AKB12が、そのようなKを直接与えるわけではありませんが、AKB12を変形することによりKを作ることができます。埋め込みによりHはKの部分系となれば、安心してHを調べることが出来ます。

僕にとってちょっと驚きだったのは、単純で分かりやすいことを基準に選んだ事例Hが、それを合理化するために3次元の圏を必要としたことです。この記事では、その合理化の基本となる圏AKB12を構成します。

ニ角三角複体

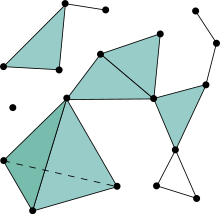
2次元の単体複体は、点、線分、三角形から構成される図形（とその組み合わせ構造）です。それぞれの次元（0, 1, 2）の構成素を、0次元単体、1次元単体、2次元単体とも呼ぶので、それらの複合体を単体複体（simplicial complex）と呼ぶわけです。次の図は、Wikipedia項目「複体」からの拝借です。これは、3次元単体（四面体）も含まれるので3次元単体複体の例ですね。

*1

2次元単体複体は、三角形を少なくとも1つは含むので三角複体とも呼ぶことにします。そして、三角形以外に二角形も許す2次元複体を二角三角複体と呼びます。二角形（二辺形ともいう）とは、半円板 {(x, y)∈R2 | x2 + y2 ≦ 1 かつ y ≧ 0} と同相な図形です*2。点(1, 0)と点(-1, 0)が頂点で、上半円と2つの頂点を結ぶ線分が辺です。次は二角三角複体の例です。

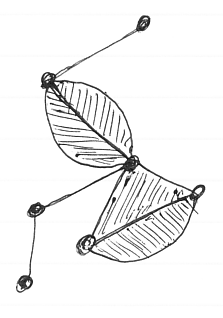
二角形を許すと、単体複体や単体写像の定義も変わってきます。しかし、相手は2次元図形なので、直感で類推することはできるでしょう。ここで詳細は述べません。

これから考える複体は有限個の単体（二角形も単体に含める）からなるものに限ります。Kが二角三角複体だというとき、Kは点集合ではなくて組み合わせ構造を表すとします。Kの幾何的点集合は|K|と表します。|K|は位相空間で、複体Kの台空間と呼びます。|K|を多面体とか多角形と呼ぶことがありますが、ここでは「台空間」を使います。

二角形は要るのか

2次元複体のセルとして二角形を許すことにしました。これは必要でしょうか？ 三角形と二角形を許すと、単体的方法と球体的方法の両方を使えるんじゃないだろうか、とうっすらと思っています。ですが、必須かどうかはよく分かりません。僕は二角形を使ってますが、無しで済ませられる可能性もあります。二角形を入れると、定義や定理の変更が必要になります。その労力をかける利便性があるかどうかも考慮しないといけませんしね。今のところ、ハッキリ分かりません。

一点複体と折れ線複体

二角三角複体は、少なくとも1つの2次元単体（二角形または三角形）を含みます。二角三角複体より次元が低くて、もっと簡単なものを導入しましょう。

まずは一点だけからなる0次元複体。これはとても簡単ですね。Pが一点複体なら、その台空間は当然一点だけからなる空間です。「複体」とか「空間」とか言うのがおこがましいほどに単純です。

nを正の整数として、実数直線内の区間[0, n]と、その有限部分集合{0, 1, ..., n}の組み合わせは1次元単体複体とみなせます。n個の辺と(n + 1)個の頂点からなるグラフ構造です。この1次元複体を今後（記号の乱用で）[0, n]で表します。

複体[0, n]と同型な複体を折れ線複体、または単に折れ線と呼ぶことにします。正の整数nは折れ線の長さと呼ぶことにしましょう -- ただし、距離をベースにした長さではなくて、含まれる1次元単体の個数のことを長さと呼ぶだけです。Kが折れ線だというときには、[0, n]からの同型単体写像 k:[0, n]→K を一緒にした(K, k)を考えることにします。単体写像（同型） k:[0, n]→K を、折れ線Kの構造写像と呼びます。

(K, k)が長さnの折れ線のとき、頂点k(0)を始点（始頂点、始端点）、頂点k(n)を終点（終頂点、終端点）と呼びます。(K, k)を単にKと略記することにして、構造写像kを表に出さない書き方をすることにします。

  • K.i := k(i) （0≦ i ≦n）
  • K.[i, j] := k([i, j]) （0≦ i ＜ j ≦n）

この書き方では、

  • Kの始点 = K.0
  • Kの終点 = K.n （nはKの長さ）
  • Kの最初の辺 = K.[0, 1]
  • K = K.[0, n]

K, Lを、それぞれ長さn, mの折れ線複体として、K.nとL.0を同一視して貼り合わせた折れ線複体をK・Lで表します。これは2つの折れ線の連接です。K・Lの構造写像 [0, n + m]→K・L も自然に定義できます。

ビーズ玉とビーズ複体

Dは二角三角複体だとします。f:[0, n]→D, g:[0, m]→D （n, mは正整数）は単射単体写像とします。次の条件を満たすとき、(D, f, g)をビーズ円板複体（bead disk complex）、または単にビーズ円板、あるいはビーズ玉と呼びます。

  1. 複体Dの台空間|D|は、円板 {(x, y)∈Rn| x2 + y2 ≦ 1} と同相である。
  2. f(0) = g(0), f(n) = g(m) である。
  3. fの像とgの像の共通部分は{f(0), f(n)}である。
  4. fの像とgの像の合併はDは1次元部分複体Sとなるが、Sの台空間|S|は、|D|の位相的境界（円周と同相な図形）と一致する。

この条件から、ビーズ円板の境界は次の構造を持つことになります。

  • 円板の境界である円周上に2頂点（f(0)とf(n)）を選び、分割された半円をそれぞれn個、m個の弧に細分した組み合わせ構造を持つ。

単体写像 f:[0, n]→D と g:[0, m]→D をビーズ円板Dの構造写像と呼びます*3。ビーズ円板全体は、二角形と三角形に分割されています。その分割は、境界では構造写像で与えられる分割と一致する必要がありますが、内部の分割方法は自由です。

ビーズ円板がユークリッド空間に埋め込まれていることは要求しませんが、便宜上次の言葉を使うことにします。

  • f(0)はDの頂点になるが、この頂点を左端点と呼び、D.leftと書く。
  • f(n)はDの頂点になるが、この頂点を右端点と呼び、D.rightと書く。
  • fの像である1次元部分複体をトップ境界と呼び、D.topと書く。
  • gの像である1次元部分複体をボトム境界と呼び、D.bottomと書く。

D1とD2が2つのビーズ円板として、D1・D2 を、D1の右端点とD2の左端点を同一視（貼り合わせ）して作った複体としまし。Dがビーズ円板、Lが折れ線のとき、Dの右端点とLの始点を同一視した図形を同じ記号・を使ってD・Lと書くことにします。L・Dも同様です。より一般に、X1, X2, ..., Xk がビーズ円板か折れ線のとき、X1・X2・ ... ・Xk が定義できます。この形の複体をビーズ複体（bead complex）、または単にビーズ（beads）と呼ぶことにします。単一のビーズ円板も折れ線もビーズ複体とみなします。ビーズ円板は“ビーズ玉1個だけ”、折れ線は“糸だけ”のビーズ複体です。

*4

念のため注意しておくと、上の写真のリアル・ビーズ玉は3次元の存在ですが、ビーズ円板＝2次元的ビーズ玉は2次元の二角三角複体です。

Lが長さnの折れ線複体のときも, ビーズ玉と同じ記法 left, right, top. left を使えるようにしましょう。

  • L.left := L.0
  • L.right := L.n
  • L.top := L
  • L.bottom := L

さらに、X1・X2・ ... ・Xkがビーズ複体のとき、

  • (X1・X2・ ... ・Xk).left := (X1).left
  • (X1・X2・ ... ・Xk).right := (Xk).right
  • (X1・X2・ ... ・Xk).top := (X1).top・(X2).top・ ... ・(Xk).top
  • (X1・X2・ ... ・Xk).bottom := (X1).bottom・(X2).bottom・ ... ・(Xk).bottom

それぞれ、ビーズ複体の左端点、右端点、トップ境界、ボトム境界と呼びます。

ビーズ複体にも構造写像を定義します。適当な正整数Nに対して、(X1・X2・ ... ・Xk).top は複体として[0, N]と同型になります。同様に適当な正整数Mに対して、(X1・X2・ ... ・Xk).bottom と[0, M]は同型です。この同型を与える単体写像を埋め込みと解釈した写像を f:[0, N]→(X1・X2・ ... ・Xk), g:[0, M]→(X1・X2・ ... ・Xk) として、ビーズ複体(X1・X2・ ... ・Xk)の構造写像と定義します*5。ビーズ玉の構造写像（の成分）f, gは単射ですが、ビーズ複体の構造写像は単射とは限りません。[追記]嘘でした。f, gは個別に見れば単射ですね。fとgを貼り合わせて、円周からの写像と見ると単射じゃないと言いたかった。[/追記]

ビーズ複体をKとするとき、その構造写像を対応する小文字kに下付き添字0, 1を付けてk0, k1のように書くことにします。

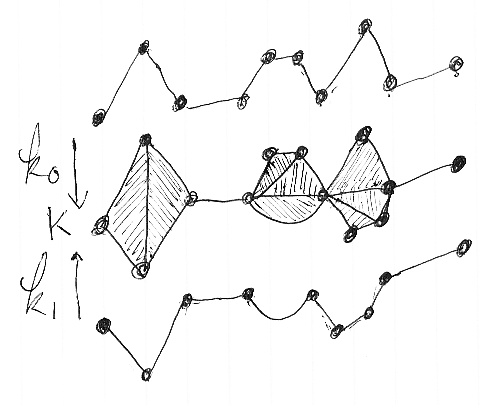
従順な複体と従順な単体写像

今まで定義した一点複体、折れ線複体、ビーズ複体をあわせて従順な複体と呼びます。折れ線複体はビーズ複体の特殊なものですから、「従順な複体とは、一点複体かビーズ複体だ」と言っても同じです。従順複体の台空間は、2次元までの連結かつ単連結な位相空間ですから、図形としては単純なものです（ホモトピー的には一点と同値になってしまいます）。

従順な複体のあいだの従順な単体写像を定義します。短く従順写像とも呼びます。

まず、基本的な従順写像を列挙します。次のようなfが基本従順写像です。

  1. 一点複体のあいだの単体写像 f:P→Q （自明な写像）
  2. Pが一点複体、Lが折れ線複体のとき、f(Pの一点) = L.0 である単体写像 f:P→L
  3. Pが一点複体、Lが折れ線複体のとき、f(Pの一点) = L.n （nはLの長さ）である単体写像 f:P→L
  4. L, Kが折れ線複体のとき、同型単体写像で構造写像を保つ*6 f:L→K。つまり、L, Kの構造写像をl, kとすると、l;f = k。
  5. Lが折れ線複体、Kがビーズ複体のとき、LとK.topのあいだの同型を与える単体射像で構造写像を保つ f:L→K。つまり、Lの構造写像をl、Kの構造写像をk0, k1とするとき、l:f = k0。
  6. Lが折れ線複体、Kがビーズ複体のとき、LとK.bottomのあいだの同型を与える単体射像で構造写像を保つ f:L→K。つまり、Lの構造写像をl、Kの構造写像をk0, k1とするとき、l:f = k1。
  7. L, Kがビーズ複体のとき、同型単体写像で構造写像を保つ f:L→K。つまり、L, Kの構造写像をl0, l1、Kの構造写像をk0, k1とすると、l0;f = k0, l1;f = k1。

基本的な従順写像の結合（合成）として得られる写像はすべて従順であると定義します。従順写像はすべて単射で、同型か境界への埋め込みです。定義から、従順写像の結合は従順で、恒等写像は従順です。したがって、従順複体とそのあいだの従順写像の全体は圏となります。この圏をAK（amenable komplexから）とします。AKは通常の圏です。

  • |AK|0 = Obj(AK) = (従順複体の全体)
  • |AK|1 = Mor(AK) = (従順複体のあいだの従順写像の全体)

従順複体の従順コスパン

圏AKが定義できたので、AK内のスパンと入れ子のスパンを定義します。|AK| = |AK|0 = (従順複体の全体) でした。|AK|の部分集合として、|AK|(0), |AK|(1), |AK|(2) を定義します。

  • |AK|(0) = 一点複体の全体
  • |AK|(1) = 一点複体または折れ線複体の全体
  • |AK|(2) = すべての従順複体（一点複体またはビーズ複体の全体）

​|AK|(0) ⊆ |AK|(1) ⊆ |AK|(2) = |AK| という包含系列があることに注意してください。|AK|(i) は、i次元以下の従順複体の全体という意味です。

コスパンとは、f:L→K, g:R→K の組み合わせですが、L-f→K←g-R という形で書くことにします。射の名前が不要なときは、L→K←R とも書きます。圏AK内のコスパンを従順コスパンと呼ぶことにします。

ここで、今までとは文字・記号の使い方を変えて、次の約束をします。

  • P, Qなどは一点複体とする。記号の乱用で、台空間|P|も、台空間の唯一の要素もPで表すことがある。
  • a, bなどは折れ線複体とする。一点複体 [0, 0] = {0} も特殊な折れ線複体と考える。[0, 0]と同型な複体（一点複体）も特殊な折れ線複体とみなす。折れ線とみなした一点複体の構造写像は、[0, 0] = {0} からの唯一の写像とする。
  • A, B, Kなどはビーズ複体とする。[0, 0]を折れ線複体とみなしたので、[0, 0]と同型な複体（一点複体）も特殊なビーズ複体とみなす。ビーズ複体とみなした一点複体の構造写像は、[0, 0] = {0} からの唯一の写像の（同じもの2つの）ペアとする。

以上の再定義から、次のように言えます。

  • 一点複体とは、0次元の従順複体である。
  • 折れ線複体とは、1次元の従順複体だが、0次元複体は自然に折れ線複体とみなせる。
  • ビーズ複体とは、2次元の従順複体だが、0, 1次元複体は自然にビーズ複体とみなせる。

さて、従順コスパンを次のように分類します。

  • P, Q∈|AK|(0)、a∈|AK|(1) である従順コスパン P→a←R を0-1-従順コスパンと呼ぶ。
  • a, b∈|AK|(1)、K∈|AK|(2) である従順コスパン a→K←b を1-2-従順コスパンと呼ぶ。

P, Q∈|AK|(0)、a, b∈|AK|(1)、K∈|AK|(2) に対して3つのコスパンからなる系 (P→a←Q, P→b←Q, a→K←b) が0-1-2-従順コスパンだとは：

  1. P→a←Q は0-1-従順コスパン
  2. P→b←Q は0-1-従順コスパン
  3. a→K←b は1-2-従順コスパン

これから使うコスパンは、0-1-従順コスパンと0-1-2従順コスパンです。1-2-従順コスパンは、0-1-2従順コスパンを定義する手段に使っただけです。

弱2-圏としてのAKB12

AKB12は3次元の圏ですが、いきなり3次元だと難しいので、2次元の圏としてのAKB12を最初に定義しましょう。2次元の圏としてのAKB12の構成素は次の通りです。

  • |AKB12|0 = |AK|0 = (一点複体の全体)
  • |AKB12|h1 = (AKの0-1-従順コスパンの全体)
  • |AKB12|hv2 = (AKの0-1-2-従順コスパンの全体)

下付きのh1, hv2は単に1, 2でもいいのですが、後の3次元のときの記法と合わせるためにこうしています。

弱2-圏の記述には、比較的最近の記事「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き）」にだいたい従いますが、多少の変更をします。

  • unitP, ida の代わりに unit[P], id[a] を使う。記法を合わせるために、dom[A], cod[A] とする。
  • 2-圏の縦結合の記号は「#」とする。「;」は第3方向（transversal方向）の結合に使うので。

P, Q∈|AKB12|0 に対して、ホム圏AKB12(P, Q)を定義します。AKB12(P, Q)は通常の圏で、次のように定義されます。

  • |AKB12(P, Q)|0 := (0-1従順スパン P→a←Q の全体)
  • |AKB12(P, Q)|1 := (0-1-2従順スパン (P→a←Q, P→b←Q, a→K←b) の全体)
  • dom[(P→a←Q, P→b←Q, a→K←b)] := P→a←Q
  • cod[(P→a←Q, P→b←Q, a→K←b)] := P→b←Q
  • id[P→a←Q] := (P→a←Q, P→a←Q, a→a←a)
  • (P→a←Q, P→b←Q, a→K←b);(P→b←Q, P→c←Q, b→L←c) := (P→a←Q, P→c←Q, a→M←c)、ここでMは、KとLのbによるコファイバー和（貼り合わせ、pushout）

ホム圏AKB12(P, Q)内での結合演算の記号は「;」を使いましたが、弱2-件全体でみたときは「#21」と書くことにします。ややこしいのですが、ひとつのホム圏だけを見たときと、弱2-圏全体と見たときで記号法を変えるほうが整合的になるのです。(弱)3-圏の記号法と合わせる意味もあります。

という次第で：

  • #21 ： 1-射（ホム圏では対象）を介して隣接する2つの2射（ホム圏では射）のコファイバー和で与えられる結合。縦結合（vertical composition）と呼ぶ。

うるさいことを言うと、縦結合を定義するコファイバー和は同型を除いて一意にしか定まらず、結合律と単位律が厳密に成立する保証がありません。それと、ホムセットのサイズの問題もありますが、気にしない方向で。

横方向の演算として、1-射（ホム圏内では対象）の横結合 |AKB12(P, Q)|0×|AKB12(Q, R)|0→|AKB12(P, S)|0 と2-射（ホム圏内では射）の横結合 |AKB12(P, Q)|1×|AKB12(Q, R)|1→|AKB12(P, S)|1 が必要ですが、いずれもコスパンのコファイバー和で定義します。

横結合の演算記号は次のようにしましょう。

  • *10 ： 0-射（対象）を介して隣接する2つの1-射（ホム圏では対象）の横結合
  • *20 ： 0-射（対象）を介して隣接する2つの2-射（ホム圏では射）の横結合

P∈|AKB12|0 に対して、unit[P]∈AKB12(P, P) は次のように定めます。

  • unit[P] := (P→P←P, P→P←P, P→P←P)

縦方向の結合に関する結合律／単位律が弱い（up-to-iso）ことを許容すれば*7、AKB12は弱2-圏になります。（細部まで確認するには退屈な作業が必要です。）

3-圏としてのAKB12

いよいよAKB12を3次元の圏にします。これ以降、3-圏は弱3-圏の意味で使い、いちいち「弱」は付けません。圏が備える第3の方向であるtransversal方向をt-方向と略称します。追加する射は：

  • t1-射 ： 対象から対象へのt-方向の射
  • ht2-射 ： h1-射（横射）からh1-射へのt-方向の2-射
  • 3-射 ： hv2-射からhv2射へのt方向の射

これらの射は、複体の単体写像として与えます。見返さなくてもいいように、冒頭の絵（ペースティング図）を再掲します。


  • 対象PからQへのt1射 ： 一点複体PからQへの単体写像（自明）
  • h1-射aからbへのht2-射 ： 折れ線複体aからbへの単体写像で、左端点を左端点に、右端点を右端点に写すもの
  • hv2-射AからBへの3-射 ： ビーズ複体AからBへの単体写像で、左端点を左端点に、右端点を右端点に、トップ境界をトップ境界に、ボトム境界をボトム境界に写すもの

t-方向を持つ射であるt1-射、ht-2射、3射は、いずれも写像です。t-方向の結合は写像の結合として定義します。

  • ;10 ： 0-射（対象）を介して隣接する2つのt1-射のt-結合（写像の結合）
  • ;21 ： h1-射を介して隣接する2つのht2-射のt-結合（写像の結合）
  • ;32 ： hv2-射を介して隣接する2つの3-射のt-結合（写像の結合）

ht2-射は横方向（h-方向）に結合することができます。3-射は横方向と縦方向（v-方向）にも結合できます。よって、次の結合演算があります。

  • *21 ： t-1-射を介して隣接する2つのht2-射の横結合
  • *31 ： t-1-射を介して隣接する2つの3-射の横結合
  • #32 ： ht2-射を介して隣接する2つの3射の縦結合

3-圏の構造の整理

AKB12は、方体（cube）ベースの三重圏から、縦1-射の概念を取り除いた構造をしています。通常の圏のように、「dom（域）, cod（余域）, id（恒等）, comp（結合）」の4つ組だけでは記述できません。この記述の煩雑性が高次圏を扱うときの困難さの要因です。

高次圏の次元について -- toward 量子と古典の物理と幾何＠名古屋」述べた次元（むしろグレード）の値は、AKB12の場合、次の6種です（6種とも既に使ってます。）v方向はありますが、v1-射はありません。v1-射は0射に退化しているのです。

  1. 0
  2. h1
  3. t1
  4. hv2
  5. ht2
  6. 3

記述を整理するひとつの方法は、方向と次元を添字にする方法です。「添字が付いたdom, cod, id, comp」で圏の構造を記述できます。しかし、添字だとイメージが湧かないので辛い面もあります。方向、次元ごとに名前や記号を変えたほうが親しみやすいかも知れません。

ここでは、添字方式と別名方式を併置してみます。別名（別記号）は次のようにします。

  • h方向のdom/codにleft/rightを使う。
  • v方向のdom/codにtop/bottomを使う。
  • h方向のidにunitを使う。
  • v方向のidにtriv（trivial）を使う。
  • t方向にはdom/cod/idを使う。
  • h方向の結合は*を使う。
  • v方向の結合は#を使う。
  • t方向の結合は;を使う。
  • それでも区別しにくいときは、次元（グレード）を添字に使う。

では、AKB12に登場する「dom, cod, id, comp」を列挙しましょう。AKB12は球体（globular）スタイルでも方体（cubical）スタイルでもないので、構成素を列挙する単純な方法がありません*8。3次元なので目視と手作業でなんとかなりますが、体調や機嫌が悪いと間違えます（もし後で間違いに気づいたら修正します）。

AKB12の「dom, cod」は次のようです。写像のプロファイル（域と余域）は、次元（グレード）だけ記しています。別名はオーバーロード（同じ名前の多義的使用）しています。

写像 プロファイル 別名
h-domh10 h1 → 0 left
h-codh10 h1 → 0 right
v-domhv2h1 hv2 → h1 top
v-codhv2h1 hv2 → h1 bottom
h-domhv20 hv2 → 0 left
h-codhv20 hv2 → 0 right
t-domt10 t1 → 0 dom
t-codt10 t1 → 0 cod
h-domht2t1 ht2 → t1 left
h-codht2t1 ht2 → t1 right
t-domht2h1 ht2 → h1 dom
t-codht2h1 ht2 → h1 cod
h-dom3t1 3 → t1 left
h-cod3t1 3 → t1 right
v-dom3ht2 3 → ht2 top
v-cod3ht2 3 → ht2 bottom
t-dom3hv2 3 → hv2 dom
t-cod3hv2 3 → hv2 cod

このなかで次元を2下げる写像は、他の写像の組み合わせで書けますが表に入れています。

次は「id」を表す写像達です。id写像は、次元の低い従順コスパンを次元の高い従順コスパンにみなすことによる埋め込みで与えられます。

写像 プロファイル 別名
h-id0h1 0 → h1 unit
v-idh1hv2 h1 → hv2 triv
t-id0t1 0 → t1 id
t-idh1ht2 h1 → ht2 id
h-idt1ht2 t1 → ht2 unit
t-idhv23 hv2 → 3 id
v-idht23 ht2 → 3 triv

そして「comp」を表す写像達。写像と×に付いてる下添字は、隣接境界となる射（セル）の種類です。

写像 プロファイル 別記号
h-comph10 h1×0h1 → h1 *10
h-comphv20 hv2×0hv2 → hv2 *20
v-comphv2h1 hv2×h1hv2 → hv2 #21
t-compt10 t1×0t1 → t1 ;10
t-compht2h1 ht2×h1ht2 → ht2 ;21
h-compht2t1 ht2×t1ht2 → ht2 *21
h-comp3t1 3×t13 → 3 *31
v-comp3ht2 3×ht23 → 3 #32
t-comp3hv2 3×hv23 → 3 ;32

いやー、めんどくさいですね。

上記にまとめたものは、いわば素材です。これらの写像のあいだに様々な法則があります。通常の圏（1-圏）の場合、法則を書き下すのは大した手間ではありませんが、3-圏の法則は数が膨大になり、書き下すのは大変です。ここでは省略しますが、グロンディ／パレ（Marco Grandis, Robert Paré）の論文 https://arxiv.org/abs/1412.0144 などを参考にしてください。AKB12は、グロンディ／パレ論文で扱っているintercategoryのv-方向を1点に潰した形をしています。

何の役に立つのか

長々と説明した割には、AKB12の素材を列挙しただけでした。退屈な話だったかも知れませんが、もっとキチンと定義しようとすると、さらに退屈な話が続くことになります。高次圏とはそういうものです。定義するだけでもけっこうな手間がかかるものなのです。

そんな手間をかけるのは、他の定義や計算を合理化したいからです。高次圏のなかで計算することなんてあるのか？ と言うと、けっこうあるんですよ。以前弱2-圏の例を10種だしましたが、オートマトンの圏は情報科学に由来します。圏の圏や（10種に入れてなかった）プロ関手の圏もプログラム意味論に使われます。コボルディズムの圏（幾何的次元が0はなくて1, 2, 3あたり）は数理物理学で使われます。双加群の圏は代数で重要です。

弱2-圏でモデル化すべき例が色々ありますが、2-圏では足りないことも珍しくはありません。そう、3-圏の出番なんですね。ただし、3-圏の構成素や法則をフルに使う必要はなくてその一部の力を借りれば済むことも多いです。そのため3-圏の存在は意識されないこともあります。別に意識されないならそれでもいいとは思いますが、「背後に3-圏があるぞ」と言ってみたい気分になったり、ね。

*1:画像は https://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Simplicial_complex_example.svg/220px-Simplicial_complex_example.svg.png

*2:別に半円版でなくてもいいです。円板でもいいのですが、円板だと、頂点が「角」の感じがしない、というだけの理由で半円板にしました。

*3:構造写像の定義域を、(n + m)個の弧に分割された円周と考えて定義してもいいです。関連する定義を修正する必要がありますが。

*4:画像は http://www.webcortex.com の http://ecx.images-amazon.com/images/I/410RFQ477QL.jpg

*5:構造写像の定義域を、(N + M)個の弧に分割された円周と考えて定義してもいいです。関連する定義を修正する必要がありますが。

*6:「構造写像を保つ」は「向きを保つ」と言っても同じです。しかし、「向き」という概念を定義しなかったので、構造写像を使って向きの概念を代用しています。

*7:transversal方向では厳密な法則が成立し、transversal方向の同型による弱結合律と弱単位律が成立します。

*8:いったん方体スタイルで考えて、一部を潰していけばよさそうです。