マルコフ圏、ベイズの定理、陰関数定理 - 檜山正幸のキマイラ飼育記 (はてなBlog)

マルコフ圏に出会って10日くらいですが、だいぶ気に入ってます。

フリッツ〈Tobias Fritz〉がマルコフ圏という俯瞰図を与えてくれたおかげで、圏論的確率論の地勢がだいぶスッキリと見えるようになりました。

マルコフ圏の枠組みから眺めると、ベイズの定理と陰関数定理はだいたい同じものです。これは、少なくとも僕にとっては、思いも寄らなかったことで、「おー、やるなぁ、マルコフ圏」とテンション上がる事態です。

内容：

マルコフ圏におけるベイズの定理
ちょっと記法の準備
多様体と非決定性写像の圏
多様体に関するベイズの定理
陰関数定理
おわりに

マルコフ圏におけるベイズの定理

「マルコフ圏 A First Look -- 圏論的確率論の最良の定式化」にて：

マルコフ圏の公理だけでは、条件付き確率の議論が出来ません。が、現状では、条件付き確率の公理化をどうすべきかの確たる方針がないので、条件付き確率を公理化するのは時期尚早です。マルコフ圏の上に条件付き確率らしきものを載せてトライアルをすべきです。

ベイズの定理は条件付き確率*1に関わる命題なので、これを記述するには、マルコフ圏に「条件付き確率らしきもの」を載せる必要があります。フリッツは、ベイズの定理（に相当する命題）を公理として要請して、“ベイズの定理が成り立つマルコフ圏”（特に名前は付いてない）のなかで条件付き確率を云々〈うんぬん〉しています。

ベイズの定理というと、次のような等式を思い浮かべる人が多いでしょう。

[等式 A] P(A∩B) = P(B|A)P(A)

この等式は、なんだかワケワカランですね。フリッツの論文の39ページにあるベイズの定理（相当命題）は、次の図（[図 B] とします）です。

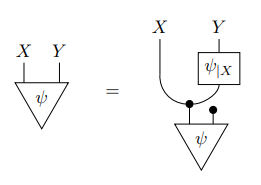
えっ、もっとワケワカランって？そんなことありません。ストリング図を約束に従って解釈すれば、この絵図等式は極めて明確な意味を持ちます。ちなみに、下から上の向きなのでそれは注意してください（「双対や随伴に強くなるためのトレーニング」参照）。

[図 B]のψやψ_|Xをマルコフ核*2（測度論的な積分核）だと思って、dx, dy記法（「ライプニッツの微分記法とアインシュタインの総和規約を測度に使ってみる」参照）を使ってベイズの定理を書けば：

[等式 C] $\psi(dx, dy) = \int_{t\in X} \delta_t(dx)(\psi_{|X}(dy | t) ) \,\psi(dt, Y)$

今日のところは、[図 B]、[等式 C]の説明は割愛しますが、出てきた記号の意味だけは書いておきます。一般的なマルコフ圏ではなくて、たちの良い可測空間とマルコフ核の圏で解釈しています。

$X, Y$ は、たちの良い可測空間です。
$\psi(dx, dy)$ は、 $X\times Y$ 上の同時確率分布です。
$\psi(dt, Y)$ は、 $\psi(dx, dy)$ から作った周辺確率分布です。
$\psi_{|X}(dy | t)$ は、同時確率分布 $\psi(dx, dy)$ に対応する条件付き確率です。
$\delta_t(dx)$ は、点tに台を持つディラック測度です。

ちょっと記法の準備

[追記] $\psi^{!Y}$ のように書いていた周辺分布を $\psi_{!X}$ のような書き方に変更しました。 $\psi_{|X}$ （条件化）と $\psi_{!X}$ （周辺化）の目視区別がしにくくなったので注意してください。[/追記]

モノイド圏の話をするときは、ストリング図を描くのがいちばんいいのですが、チャッチャとストリング図を描く手段がないのでテキスト表現します。フリッツの論文から引用した前節の図に出てくる射をテキストで書けば：

絵図等式の左辺： ψ:1→X $\otimes$ Y （1は単位対象でもあり終対象でもある対象、 $\otimes$ はモノイド積）
絵図等式の右辺の下側の三角形、右ワイヤーが途切れてるヤツ： (id_X $\otimes$ !_Y) $\circ$ ψ （!_Xは、Xから1への唯一の射）
絵図等式の右辺の中段の三又： Δ_X:X→X $\otimes$ X （対角写像）
絵図には現れない： ρ_X:X $\otimes$ 1→X （モノイド圏の右単位律子〈right unitor〉）

以上のように約束すると、[図 B]は次のようにテキスト表現できます*3。

$\psi = (\mbox{id}_X \otimes \psi_{|X})\circ \Delta_X \circ \psi_{!X} : {\bf 1} \to X\otimes Y$
$\psi_{!X} := \rho_{X} \circ (\mbox{id}_X \otimes !_Y)\circ \psi : {\bf 1} \to X$

この等式は、圏に、 $\otimes$ （モノイド積）、1（単位対象兼終対象）、Δ_X（対角射）、!_X（終対象への射）があれば意味を持ちます。しかし、この等式を成立させる ψ_|X の存在は一般には保証されません。存在を主張したいなら、証明するか、または公理として要請します。

多様体と非決定性写像の圏

「マルコフ圏って、いいんじゃないのコレ」において、計算科学でしばしば使われる圏としてNonDet（集合と非決定性写像の圏）を出しました。NonDetの射である非決定性写像 F:X→Y とは次のようなものです。

x∈X に対して、F(x) はYの部分集合である対応

Yのベキ集合を Pow(Y) として、F(x)∈Pow(Y) なので、F:X→Pow(Y) という写像だともいえます。通常の写像の値が単一要素だったのを、部分集合を許すようにしたのが非決定性写像です。

さてここで、なめらかな多様体となめらかな写像の圏をManとして、次の“比例式”を考えます。

Set : NonDet ＝ Man : ？

疑問符のところには何が入るでしょうか？答は、「対象は多様体だけど、射として非決定性写像を許すような圏」ですよね。って、多様体のあいだの非決定性写像ォー、はーっ、ワケワカラン！

ワケワカランのですが、そんな圏が在りそうな気がします。ここは楽観的に在ると信じて、当該の圏をNonDetManとしましょう。|NonDetMan| = |Man| = (すべての多様体) で、Manは、NonDetManに自然に埋め込めます。

X, Y が多様体として、非決定性写像〈non-deterministic map〉（そんなものが在るとする） F:X→Y の値 F(x) はYの部分多様体になります。Yのすべての部分多様体からなる集合を Subman(Y) とすると、F:X→Subman(Y) と考えてもかまいません。Subman(Y) は通常の意味の多様体にはなりませんが、なんらかの意味で“なめらか構造”を持つとして、F:X→Subman(Y) は“なめらか”とします。

a, b∈X に対して、F(a)∈Subman(Y) と F(b)∈Subman(Y) の次元が違うと扱いにくそうなので、とりあえずは F(x) の次元はxによらず一定を仮定してもいいでしょう*4。xによらず dim(F(x)) = k であるような非決定性写像をk次元の非決定性写像〈non-deterministic map of dimension k〉と呼ぶことにします。π:Y→X がファイバー次元kのファイバーバンドルのとき、逆向きの対応 X→Subman(Y) は、k次元の非決定性写像の良い例になるでしょう。古典的な線織面は、次元1（値が直線）の非決定性写像になります。

非決定性写像 F:X→Y in NonDetMan に対する形容詞全域〈total〉、全射的〈surjective〉、単葉〈univalent〉などは、NonDetと同じ定義です。

任意の x∈X に対して、

F(x) が連結部分多様体ならば、F は連結値非決定性写像〈connected-value non-deterministic map〉
F(x) がコンパクト部分多様体ならば、F はコンパクト値非決定性写像〈compact-value non-deterministic map〉
F(x) が開集合ならば、F は開値非決定性写像〈open-value non-deterministic map〉

と呼ぶことにします。

一点多様体1からの非決定性写像 1→X は、Xの部分多様体と同じです。0次元の連結値非決定性写像は、決定性写像と同じです。0次元のコンパクト値非決定性写像は、一点が有限分散〈有限分岐〉する非決定性写像です。Iを0次元離散多様体として、F:I→X が全射的開値非決定性写像なら、FはXの開被覆です。

実際のところNonDetManは正体不明ですが、発見的方法の手段として使うくらいは許してちょうだい。

多様体に関するベイズの定理

仮にNonDetManが存在したとして（思考実験）、NonDetManでベイズの定理は成立するでしょうか？ -- 全然成立しません（オイッ!）。NonDetManは、フリッツが条件付き確率が扱える圏として定義した“ベイズの定理が成立するマルコフ圏”からは遠く離れた存在です。

しかし、特別に扱いやすい状況では、NonDetManでもベイズの定理が成立します。稀〈まれ〉に成立する“多様体に関するベイズの定理”が、実は陰関数定理だと僕は言いたいのです。ポイントは、うまくいく稀〈まれ〉なる状況をキチンと記述することです。

アナロジーが分かりやすいように、確率の話と多様体の話で同じ記号を使い、用語も出来るだけ揃えましょう（揃ってないモノもあります）。

記号	確率の話	多様体の話
X, Y	可測空間	多様体
X×Y	直積可測空間	直積多様体 *5
F:X→Y	マルコフ核	非決定性写像
1 = {0}	一点可測空間	一点多様体
ψ	同時確率分布	同時部分多様体
!_Y	終写像	終写像
Δ_Y	対角写像	対角写像
ψ_!X	周辺確率分布	周辺部分多様体
ψ_\|X	条件付き確率	陽関数

さて、“特別に扱いやすい状況”を記述しましょう。もとになる同時部分多様体（直積多様体の部分多様体）ψ:1→X×Y in NonDetMan は次のような性質を持つとします。

ψ(0) = Z ⊆ X×Y とすると、Zは通常の部分多様体。
第一射影 π¹:X×Y→X を、Z上に制限したものを同じ記号で π¹:Z→X と書く。
π¹:Z→X は、写像として全射であり、局所微分同相写像（同じことだが、可微分エタール写像）である。局所部分同相であることから、dim(Z) = dim(X) 。

この前提が満たされるなら、ベイズの定理は成立します。 $\psi = (\mbox{id}_X \otimes \psi_{|X})\circ \Delta_X \circ \psi_{!X} : {\bf 1} \to X\otimes Y$ となるような $\psi_{|X}:X \to Y$ が存在するのです。

ただし、命題の逆は言ってません。ベイズの定理が成立しても、この前提が満たされない状況はあるでしょう。が、ベイズの定理と同値になる条件が何であるかは僕はよく分かりません。

今述べた形のベイズの定理が、陰関数定理（少し一般化している）と同じことを、次節でもう少し説明します。

陰関数定理

陰関数定理を、多様体に関して述べてみます。オーソドックスな陰関数定理と少し違い、陰関数を定義する方程式が出てこないで、方程式で定義される部分多様体をいきなり出しています。方程式から部分多様体を作るステップを省略していると思ってください。

M, N は多様体として、L⊆M×N を部分多様体とします。p∈L に対して、pのM×Nにおける開近傍を取りたいのですが、開集合 X⊆M と Y⊆N を選んで、p∈X×Y をpの開近傍とします。Z := L∩(X×Y) と置きます。陰関数定理の主張は次のようになります。

うまく選んだ X, Y に対して前節の条件が成立するならば、適当な写像 f:X→Y があって、Zはfのグラフと一致する。

絵に描くと次のよう。

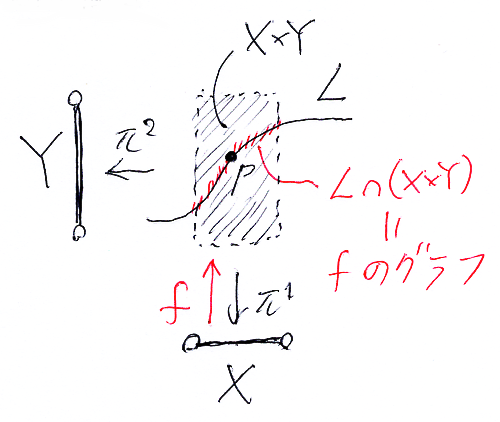
部分多様体Z（あるいはもとになった L⊆M×N）を陰関数〈implicit function〉と呼び、f:X→Y を対応する陽関数〈explicit function〉といいます。ここでの陽関数は、非決定性写像ではなくて、決定性写像です。

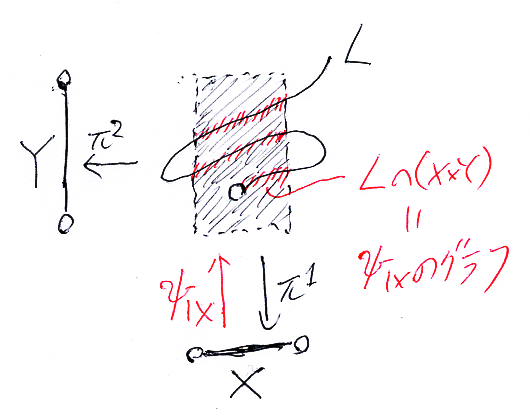
前節のベイズの定理は、上記陰関数定理をわずかに一般化していて、 $\psi_{|X}:X \to Y$ が決定性であることを要求していません。とはいえ、0次元非決定性しか出てこないので、 $\psi_{|X}:X \to Y$ はいわゆる多価関数〈多葉関数〉です。

絵に描くと次のようです。

おわりに

マルコフ圏の枠組みがなければ、ベイズの定理と陰関数定理が同一のステートメントを共有していることは気が付きにくいでしょう。これは、マルコフ圏の公理系がよくできていることへのささやかな傍証です。

謎の圏NonDetManにおいては、特別な条件がない限りはベイズの定理＝陰関数定理は成立しません。それでも陰関数定理は役に立ちます。ということは、ベイズの定理が完全には成立しない圏において、稀〈まれ〉に成立するベイズの定理でも十分に役立つ可能性があります。

なにかと妄想が捗って、マルコフ圏、いいんじゃないのコレ。

*1:「条件付き確率」は、文脈により幾つかの異なった意味を持つ多義語です。相当に違った意味で同じ語が使われるので注意してください。

*2:マルコフ核の同義語が山のようにあることは、「ベイズ確率論、ジェイコブス達の新しい風 // チャンネルについてもう少し」を参照。

*3:[追記]二番目の等式に $(\rho_X)^{-1}$ とありましたが、 $\rho_X$ の間違いでした。訂正しました。[/追記]

*4:応用上は、この仮定は邪魔になりそうです。様々な次元の部分多様体が値になるようなケースが出てくるでしょうから。

*5:常に直積を可能とするには、境界なし多様体だけを考えるか、角付き多様体を考えます。