ツリーデータ型のモナド - 檜山正幸のキマイラ飼育記 (はてなBlog)

ある種のツリーデータ型はモナドにできます。

[追記]この記事は十何年か前に書いておくべきだったのかも知れません。当時は、ツリーデータ型のモナドは自明な事実に見えてました（ツリーばっかりいじっていたからなー）。が、「えっ、そうだったの」と思う人もいそうなので、思い出して記した次第。[/追記]

内容：

自由モノイド＝クリーネスター
ファイルシステム風パス記法
ツリー形状とリーフ値付きツリー
リーフ値付きツリーデータ型のモナド

自由モノイド＝クリーネスター

集合Xに対して、Xから生成される自由モノイド (M, #, ε) を定義しましょう。

モノイドの台集合Mは、Xの要素を並べた列の集合。List型構成子を知っているなら、M := List(X) 。
モノイドの演算#は、列〈リスト〉の連接〈concatenation〉。
モノイドの単位元は、空列〈空リスト〉ε 。

台集合MをX^*とも書きます。また、いつもの記号の乱用（悪習）により、

X^* = (X^*, #, ε)

写像 f:X → Y in Set に対して、モノイド準同型写像 X^* → Y^* in Monoid を構成できるので、関手 FreeMonoid:Set → Monoid を構成できます。これは、グラフからの自由圏構成 FreeCat:Graph → Cat の特別なものだとみなすこともできます -- 興味があれば、次の記事を参照してください。

X^* の右肩の星はクリーネスター〈Kleene star〉と呼ばれ、自由モノイドの台集合、自由モノイド、自由モノイド生成関手などの意味で使われます。

ファイルシステム風パス記法

具体例として次の3つの集合を考えます。

A = {a}
B = {1, 2, 3}
C = {foo, bar}

Aの要素は「文字 a」そのものなので 'a' と書いたほうがいいでしょう。同じ理由で、Cの要素は "foo", "bar" と書いたほうがいいでしょう。しかし、めんどくさいので、a, foo, bar にします。

A^*, B^*, C^* の要素をどう表しましょうか？ a, aaa∈A^*、3, 3231∈B^* とかはいいでしょうが、C^* の要素を foobarbar とか書くと区切りがわかりません。スラッシュを区切り記号に使うことにします。そうすると、ファイルシステムのパスに似ているので、行きがかり上、先頭（左端）にもスラッシュを置きます。

単なる併置	スラッシュ区切り
a	/a
aaa	/a/a/a
3	/3
3231	/3/2/3/1
foobarbar	/foo/bar/bar

空列εは単一のスラッシュ / で表します。連接演算はホントに並べるだけですが、空列との連接では余分なスラッシュを削除します。

/a # /a/a/a = /a/a/a/a
/ # /a/a/a = /a/a/a
/ # / = /

ツリー形状とリーフ値付きツリー

ツリー形状〈tree shape〉がどんな形であるかは説明しません。皆さんの直感的理解で十分です。一例を挙げれば、次の図形はツリー形状です。

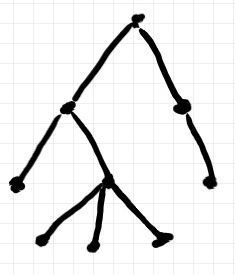
ツリー形状は、何の装飾もない“裸のツリー”のことです。ツリー形状は、ルートからリーフ〈葉〉へと向かう方向を考えて有向グラフになります。ツリー形状への修飾として、すべての辺にラベルを付けます。辺ラベルの集合をXとします。

ツリーのすべてのノードが辺ラベルの列で一意的に表現できるように、次の制限を付けます。

ひとつのノードから出る辺の本数は、集合Xの基数〈cardinality〉を超えてはならない。

そして、ラベリングは実際にノードが一意的に表現できるものに限ります。兄弟辺に同じラベルが付くのはダメです。

辺ラベルの集合Xが無限集合なら、上記の基数に関する制限は常に満たされます。辺ラベルの集合に、A = {a} や C = {foo, bar} を使うと、上の例のツリー形状にラベリングできません。辺ラベルの集合に B = {1, 2, 3} を使えばOKです。上のツリー形状のすてのノードをラベル {1, 2, 3} を使ったパスで表現してみましょう。

/
/1
/1/1
/1/2
/1/2/1
/1/2/2
/1/2/3
/2
/2/1

このなかでリーフノードは次の5個です。

/1/1
/1/2/1
/1/2/2
/1/2/3
/2/1

リーフノードの意味は明らかでしょうが、ルートノードしかないツリーでは、ルートノードはリーフノードになります。

辺ラベルの集合とは別に（同じ集合でもかまわないが）集合Yを考えます。リーフノードにだけYの値を割り当てたツリーを、リーフ値付きツリー〈leaf-velued tree〉と呼びましょう。辺ラベルの集合がXであり、リーフ値の集合がYであるリーフ値付きツリー全体の集合を LVTree_X(Y) とします。

上記の例で、リーフ値の集合を C = {foo, bar} とすると、LVTree_B(C) ができます。その要素の一例は、リーフノードのパスに foo か bar に割り当てればいいので、例えば次のように書けます。

/1/1 $\mapsto$ foo
/1/2/1 $\mapsto$ foo
/1/2/2 $\mapsto$ bar
/1/2/3 $\mapsto$ foo
/2/1 $\mapsto$ bar

入れ子のリスト（囲み括弧をブラケットにする）として次のように書いてもかまいません。

[ [foo, [foo, bar, foo]], [bar] ]

[追記]↑が間違っていたので修正しました。2次元的なレイアウトを使うと間違えないかな。

          [ ]
   [ ],           [ ]
foo,   [ ]        bar
   foo, bar, foo

[/追記]

リーフ値付きツリーデータ型のモナド

ツリーの辺ラベルの集合Kを固定します。Kの要素は“キー”と呼んでもかまいません。そして、リーフ値の集合を色々と変化させます。この節での X, Y などは色々と変化させる集合です。

X $\mapsto$ LVTree_K(X) （Xは色々と変化させる集合）

という、“集合 $\mapsto$ 集合”対応は、型構成子になります。写像 f:X → Y in Set に対して、fをツリーに適用するように“マップ化”することもできます。

map(f):LVTree_K(X) → LVTree_K(Y)

型構成子とマップ化高階関数の組は関手を定義するので、この関手を同じ名前で

LVTree_K:Set → Set

とします。

集合圏上の自己関手 LVTree_K に、2つの自然変換 η, μ を付け足して、モナドにしましょう。

For X∈|Set|, η_X:X → LVTree_K(X) in Set
For X∈|Set|, μ_X: LVTree_K(LVTree_K(X)) → LVTree_K(X) in Set

η_X:X → LVTree_K(X) は次のように定義します。

x∈X に対して、「ルートノードしかないツリーで、リーフ値がxであるリーフ値付きツリー」を対応させる。

μ_X: LVTree_K(LVTree_K(X)) → LVTree_K(X) は、次のように考えます。

LVTree_K(LVTree_K(X)) の要素は、親のツリーの各リーフに子のツリーが入れ子で入っている。“親のリーフノード”と“子のルートノード”を同一視する（糊付けする）ことにより入れ子を平坦化したツリーは LVTree_K(X) の要素になる。

ラフな定義(?)ですが、お好みのプログラミング言語で実際の処理を書いてみれば実感が湧くでしょう。(LVTree_K, η, μ) がモナドになるには、モナド法則を満たす必要がありますが、その確認は練習問題とします。