モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き）

お正月に考えてみたことを記します。書くのにけっこう時間がかかりました。長いです。

圏の基本事項を学んだ後にモナドの概念が導入されます。しかし、モナド概念を使って圏を調べるということも出来そうです。「圏論 → モナド論 → 圏論」という循環が生じますが、こんな循環はしょっちゅう生じる現象なので気にする必要はありません。

狭義の圏論（あくまで狭義）とは、圏Catを調べることだと言っていいでしょう。Catには、圏、関手以外に自然変換も含まれるとして、2次元の圏と捉えましょう。2次元の圏Catよりも扱いやすかったり、豊富な構造を持つナニモノカをXCatとします。うまいXCatが見つかると、通常の圏論がより簡単になったり、より面白くなったりするかも知れません。

そんなXCatを定義し調査することを、仮に代替圏論と呼ぶことにします。ここでは、モナドの構成をヒントにして、（ひとつの）代替圏論を試みてみます。まだ詰めは甘い話です。予備知識に関して、弱2-圏（双圏）の事などけっこう説明してますが、それでもself-containedではないので、必要に応じてnLabなどを参照しながら読んでください。

この記事のアイディアは、（お正月に眺めた）次のラックの論文に基づくものです。

• Title: Composing PROPs
• Author: Stephen Lack
• Pages: 18p
• URL: http://www.tac.mta.ca/tac/volumes/13/9/13-09abs.html

内容：

モノイド、モナド、圏

モナドが一種のモノイドであることはよく知られています。モナドは、自己関手（endofunctor）の圏のなかのモノイドになっています。では、モノイドとモナドを全く同じように扱うか、というと、そうではありません。特定のモナドは特定の圏C上の自己関手圏 End_Cat(C) = Cat(C, C) 内に存在しますが、すべてのモナドを考えるときは、Cを動かさなくてはなりません。Cを小さい圏に限るなら、モナドはすべての小さい圏の圏Catの2次元構造（自然変換を含む構造）のなかに棲んでいることになります。

モナドがCat内に居る生き物であるのに対して、通常のモノイドは集合の圏Setのなかに棲んでいて、集合と写像から構成されます。モノイドとモナドの特徴をまとめると：

	モノイド	モナド
構成要素	集合と写像	圏と関手と自然変換
環境となる圏	集合圏Set	圏の圏Cat
環境となる圏の次元	1次元	2次元

モノイドとモナドは類似の構造であるが、「構造の次元が違う」と言えます。

ところで圏は、これまた一種のモノイドとみなせます。小さな圏だけを考えるとして、集合Xを対象集合とする圏Cは、Xを頂点集合とする有向グラフの圏Graph[X]のなかのモノイドとなります。モナドのときと同様に、すべての圏を考えるときは、Xを動かさなくてはなりません。このことから、モナドの構成と圏の構成に類似性があるだろう、と見当が付きます。

1. 特定の圏C上のモナドがCat(C, C)内のモノイドであるのと同様に、特定の集合X上の圏はGraph[X]内のモノイドとなる。
2. モナドと圏は、共通の構成法を持つだろう。局所的には（CやXを固定すれば）どちらもモノイドなのだから。
3. モナドが2次元の圏Cat内に棲むように、圏もなんらかの2次元の圏（生息環境）のなかに存在するのだろう。

代替圏論の枠組と効能

前節の見通しに従って、代替圏論を試みてみましょう。通常の“圏の圏”Catに代わる新しい“圏の圏”をXCatと書くことにします。Xは未知なるモノとしてのエックスと、extendedの意味で付けています。

細部の説明は後回しにして、結論を先に言ってしまうと、XCat = Lax2(1⁽²⁾, SPAN(Set)) が新しい“圏の圏”の定義です。この定義は、モナドの全体が Lax2(1⁽²⁾, Cat) と書けることをヒントにしたものです。より一般には、（小さいとは限らない）双圏Bに対して Lax2(1⁽²⁾, B) という構成法があり、その2つの事例がモナドと圏の構成法になっています。

XCatが通常のCatよりメリットがある点を述べておきます。Lax2(1⁽²⁾, SPAN(Set)) という定義のなかに、集合圏Setが含まれますが、これは終対象とファイバー積（プルバック）を持つ任意の圏*1に置き換えることができます。つまり、XCatは終対象／ファイバー積を持つ圏でパラメトライズされているのです。

• XCat(C) = Lax2(1⁽²⁾, SPAN(C))

ベースとなる圏Cを取り替えることにより、Set以外をベースとした圏論を展開できます。これは、Cの内部圏の理論に対応します。XCatの定義のなかには、SPAN(-), 1⁽²⁾, Lax2(-, -) なども含まれます。これらを一般化したり取り替えることにより、別な圏概念が得られる可能性もあります。

XCatはあからさまにモナドと類似しています。なので、モナドに関する概念を圏に持ち込むことが（ある程度は）できるでしょう。例えば、ベックの分配法則により2つのモナドの複合モナドを構成できます。同様に、2つの圏の複合圏（直積や直和ではない）を構成できるかも知れません*2。テンソル強度（tensorial strength）と強モナド（strong monad）という概念に対応する強圏（strong category）という概念も定義可能かも知れません。逆に、圏同値や随伴対は圏論の概念ですが、モナド側ではどんな概念でしょうか？

思いついたばかりでロクに考えてないので、楽観的な期待感を述べているだけですが、けっこう面白い気がします。

圏論の用語法の問題点と対策

XCatの定義である Lax2(1⁽²⁾, SPAN(Set)) について説明したいわけですが、圏論の用語法の不統一性と混乱が説明とコミュニケーションの障害となります*3。今回の話では、メジャーな用語法に従うと表現が破綻してしまうので、破綻を回避する言葉づかいを選択します。用語法を改善するだけで、難解さが格段にやわらいだりします*4。

まず「n-圏」という言葉ですが、これは n = 0, 1, 2, ... に対するn次元の圏の意味です。強n-圏（strong n-category）と弱n-圏（weak n-category）という区別があります。最近では、単にn-圏というとそれは弱n-圏を意味することが多いです。また、「強」よりは「厳密（strict）」を使うことが多くなっていると思います。「弱」は「非厳密（non-strict）も許す」の意味です。ここでの非厳密とは、「イイカゲンで当てにならない」という意味では無いですよ！ 厳密性も非厳密性もチャンと（厳密に）定義された概念です。ややこしいのは、厳密n-圏を弱n-圏の特殊なモノとみなす場合（これが普通）と、「弱＝非厳密」という用法があることです。ここでは、「弱＝厳密または非厳密」です。

n = 2 の場合は例外的で、単に2-圏というと、厳密2-圏の意味です。弱2-圏は双圏と呼びます。n = 2 だけ用語法が違っているのです*5。しかも、「双」という厄介な形容詞が付いています（「「余」と「双」の使い方がバラバラ」参照）。この記事では、これから先「双圏」は使わず、弱2-圏を使います。通常の「2-圏」は厳密2-圏と形容詞「厳密」を付けます。厳密2-圏は弱2-圏の特別なモノです。厳密・非厳密が文脈から明らかなときや、厳密・非厳密を気にする必要がないときは単に「2-圏」ということもあります。

弱2-圏のあいだの関手をなぜか疑関手（pseudofunctor）と呼びます。この「擬」の用法は他の用語との統一性・整合性がまったく無いので使用せず、2-関手と呼ぶことにします。

ただし、2-関手には種類があります。この種類はモノイド圏のときと形容詞を合わせて、次のように呼びます。

1. 厳密2-関手（strict 2-functor）
2. タイト2-関手（tight 2-functor）
3. ラックス2-関手（lax 2-functor）
4. 反ラックス2-関手（oplax 2-functor）

これらの呼び名（形容詞）については、「モノイド圏の随伴性を“豊饒圏の圏”の随伴性に持ち上げる： 計画編」でも言及してます。「タイト」という形容詞は一般的ではありませんが、形容詞「強」や形容詞なしによる混乱を避けるために「タイト」を使います。

「強」の代わりに「厳密」「タイト」を使うのは、「テンソル強度を持つ（with tensorial strength）」の意味で形容詞「強」を使う習慣があり、様々な意味の「強」がかち合ってしまうからです。「強」はテンソル強度の意味だけに使うようにします。

実は、疑関手を弱2-関手（weak 2-functor）と呼ぶ人もいます。強モノイド関手の「強」を流用するなら、疑関手は強2-関手となります。すると、疑関手＝弱2-関手＝強2-関手 というハチャメチャな状況になります。この点からも、形容詞「強（strong）」は避けるべきと思います。僕の過去の記事では「強」を使っているのですが、それはご容赦ください。

モノイド圏は、単対象（対象がひとつだけ、single-object）の2-圏と考えることができます。一般の2-圏と単対象2-圏に同じ用語法を適用するようにします。これで、だいぶスッキリします。

	一般の2-圏	単対象の2-圏
厳密な圏	厳密2-圏	厳密モノイド圏
非厳密な圏	弱2-圏	モノイド圏
厳密関手	厳密2-関手	厳密モノイド関手
タイト関手	タイト2-関手	タイト・モノイド関手
ラックス関手	ラックス2-関手	ラックス・モノイド関手
反ラックス関手	反ラックス2-関手	反ラックス・モノイド関手

2-圏には、対象と射以外に2次元の構成素がありますが、これは2-射と呼ぶことにします。2-セル、または単にセルと呼ぶこともありますが、基本的な（生成元となる）2-射を2-セルと呼ぶこともあるので、今回は用語「2-射」を採用します。0-射は対象、1-射は通常の射のことです。

2-圏と2-関手の図示法

弱2-圏はモノイド圏の拡張であり、モノイド圏は弱2-圏の特殊ケースです。このため、弱2-圏の定義はモノイド圏と非常によく似ています。単対象の2-圏がモノイド圏なのですが、通常は次元をズラして記述します。この事情を表にまとめておきます。次元のズレで混乱してしまう人は多そうなので注意してください。

単対象の2-圏	モノイド圏
0-射（ただ1つ）	考えない
1-射	対象（0-射）
2-射	射（1-射）
ホム圏	モノイド圏全体
1-射の横（水平）結合	対象のモノイド積
2-射の縦（垂直）結合	射の結合
2-射の横（水平）結合	射のモノイド積

一般の2-圏（弱2-圏）とモノイド圏の違いは、対象がたくさんある（multi-object）かどうかだけです。一般の2-圏（弱2-圏＝双圏）の形式的な定義はnLabのエントリーを参照してもらうとして、ここでは2-圏の“描き方”を述べます。

ストリング図を使う場合は、2-圏の対象、射、2-射の描き方はモノイド圏の場合とほとんど同じです。異なるのは、背景色が“単色”から“多色”になるだけです。ここで背景色とは、対象（0-射、0-セル）を表す領域の色のことです。

念のために、2-圏の構成要素（constituent, entity）と図形の対応を示しましょう。

2-圏	ストリング図
対象（0-射）	面（領域）
射（1-射 ）	辺（ストリング、ワイヤー）
2-射	頂点（ドット、ボックス、丸など）

モノイド圏の場合は、暗黙の（言及されない）0-射を表す平面領域が単色（または無色）だったのに対して、2-圏では様々な色（あるいはラベル）で識別されます。

絵の実例に関しては、「絵算のススメ 2015 年末版」で紹介したマースデンの論文などを参照してください。

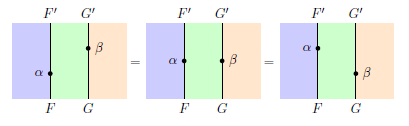
2-圏のあいだの2-関手、特にラックス2-関手の図示にはマッカーディのストライプ図を使うのが便利です。ストライプ図については、次の記事を参照してください。

• モノイド関手／ラックス・モノイド関手とその実例
• モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形
• モノイド自然変換とモノイド同値関手

次は多色のストライプ図の例です（"Frobenius Morphisms of Bicategories"より）。

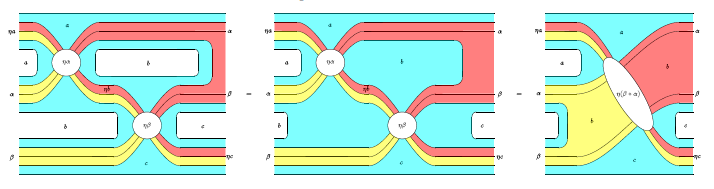
ストライプ図は、モノイド圏を含む2次元の圏とそのあいだの関手の計算に大変便利な道具です。

スパンの弱2-圏 ＝ 二部箙の弱2-圏

弱2-圏とそのあいだの関手の準備ができれば、XCat = Lax2(1⁽²⁾, SPAN(Set)) という定義の説明ができます。1⁽²⁾とSPAN(Set)は弱2-圏であり、これらの弱2-圏のあいだのラックス2-関手の全体が Lax2(1⁽²⁾, SPAN(Set)) です。（後で、Lax2(-, -)上に2-圏構造を入れますが、今は気にする必要はありません。）

まずは弱2-圏SPAN(Set)ですが、これは「スパンの圏と行列の圏」で説明しています。「スパンの圏と行列の圏」の目的は、SPAN(Set)とMAT^|Set|_Set が事実上同じであることを説明することでした。SPAN(Set)が弱2-圏（双圏）であることを強調してませんが、圏係数行列の圏とみたときの行列の積が横結合を与えます。

弱2-圏の概念	圏係数行列の圏の概念
対象	添字集合
1-射	（対象の）行列
2-射	射の行列
1-射の横結合	行列の積
2-射の縦結合	射の行列の結合
2-射の横結合	射の行列の積

集合圏Setが係数圏のとき、行列の係数（成分）は集合（1-射）または写像（2-射）となります。形式上は、通常の行列計算と同じ計算ができます。

弱2-圏SPAN(Set)は、行列表示以外の別な表示も持ちます。SPAN(Set)の1-射は箙〈えびら〉とみなせるのです。箙（quiver）は有向グラフ（directed graph）と同義です（この言葉を選んだ事情は「形容詞「複」「多」と箙〈えびら〉」、応用例は「高次圏の下部構造を箙〈えびら〉で表現してみる」を参照してください）。代替圏論のためには、SPAN(Set)を箙で解釈するのが便利です。

集合V, Eと、写像 src, trg:E→V の組 (V, E, src, trg) が箙です。頂点の集合Vを2つの集合X, Yに分けて、src:E→X, trg:E→Y としたモノを二部箙（bipartite quiver）と呼びます。もちろん、二部グラフ（bipartite graph）とも呼びます、というか、二部グラフが普通の呼び名です。

A = (X, Y, E, src, trg) を二部箙とします。二部箙の有向辺をアローとも呼びます。アローは始頂点集合Xに始点を持ち、終頂点集合Yに終点を持つことになります。x∈X, y∈Y に対して A(x, y) := {f∈E | src(f) = x, trg(f) = y} とすると、(x, y)|→A(x, y) という対応は、X×Y→|Set| となるので集合係数行列を定めます。これが、二部箙と集合係数行列を同一視する方法です。

二部箙を記述するために、X, Y, Eのような文字をたくさん消費するのはイヤなので、次のように約束します。

• 記号の乱用で、アロー（有向辺）の集合EをAと書く。（二部箙全体と同じ記号を使う。）
• X = Src(A), Y = Trg(A) と書く。
• 異なる箙に属するsrc, trgを区別したいときは、src_A, trg_Aのように添字を付ける。
• 以上の約束のもと、A = (Src(A), Trg(A), A, src_A, trg_A) と書ける。

二部箙の全体が構成する弱2-圏をBipartQuivとします。BipartQuivはSPAN(Set)と同じものです -- この2つは、メンタルモデルの違いしかないと言っていいでしょう。念のために弱2-圏BipartQuivの仕様を箇条書きにしておきましょう。|-|_iは弱2-圏を構成するi次元の構成素（i-射、i-セル）の全体の集合です。

1. Obj(BipartQuiv) = |BipartQuiv|₀ は、すべての集合からなる類である。
2. Mor(BipartQuiv) = |BipartQuiv|₁ は、すべての二部箙からなる類である。
3. X, Y∈Obj(BipartQuiv) に対して、ホム圏 BipartQuiv(X, Y) が定義できる。以下にホム圏の定義：
4. ホム圏BipartQuiv(X, Y)の対象（BipartQuivの射）は、Src(A) = X, Trg(A) = Y であるような二部箙 A = (X, Y, A, src_A, trg_B) である。
5. ホム圏BipartQuiv(X, Y)の射（BipartQuivの2-射） F:A→B は、箙のアロー集合のあいだの写像であって、srcとtrgを保存するものである。F:A→B in BipartQuiv(X, Y) を、弱2-圏BipartQuivの2-射とみるときは、F::A⇒B:X→Y と書く。
6. ホム圏BipartQuiv(X, Y)の結合（BipartQuivの2-射の縦結合）は、写像の結合（合成）である。
7. ホム圏BipartQuiv(X, Y)の恒等射（BipartQuivの恒等2-射）は、恒等写像である。
8. 二部箙（BipartQuivの1-射）(X, Y, A, src_A, trg_A)と(Y, Z, B, src_B, trg_B)の横結合は、スパンの横結合として定義する。集合Y上のファイバー積を使う。
9. BipartQuivの2-射 F::A⇒A':X→Y G::B⇒B':Y→Z の横結合は、写像のファイバー積として定義する。
10. 集合Xに対する自明な二部箙 (X, X, X, id_X, id_X) が、横結合に対する単位となる。

ホム圏BipartQuiv(X, Y)において X = Y としたエンド圏BipartQuiv(X, X)をQuiv[X] と書くことにします。するとQuiv[X]は、Xを頂点集合とする通常の箙（有向グラフ）となります（箙と有向グラフは同義なので、Quiv[X] = Graph[X]）。BipartQuivの横結合がQuiv[X]内ではモノイド積になり、Quiv[X]はモノイド圏となります。このモノイド圏Quiv[X]のなかのモノイド対象が、対象集合をXとする小さな圏となることに注意してください -- 後でこの事実を系統的に定式化します。

2-圏の例 10選

高次圏の話はどうしても抽象的になってしまうので、具体例が欲しくなります。2-圏の具体例を幾つか挙げておきます。次元0, 1, 2の構成素と三種類の結合（compositions）だけ示します。

1. 圏の圏

前節で説明したBipartQuiv（SPAN(Set)と同じ）は非厳密2-圏です。厳密2-圏の典型例は圏の圏Catでしょう。

• 対象は、（小さい）圏である。
• 射は、関手である。
• 2-射は、自然変換である。
• 射の横結合は、関手の結合である。
• 2-射の縦結合は、自然変換の縦結合である。
• 2-射の横結合は、自然変換の横結合である。

2. 順序集合の圏

順序集合の圏Ordは、厳密2-圏の例になります。Ordは簡易版Catのようなものです。「n-圏とは何だろう」の主要な例になっているので、詳細はそちらを参照してください。

• 対象は、順序集合である。
• 射は、単調写像（順序を保つ写像）である。
• 2-射は、単調写像のあいだの順序である。
• 射の横結合は、単調写像の結合である。
• 2-射の縦結合は、単調写像のあいだの順序の推移律である。
• 2-射の横結合は、単調写像の結合の順序（に関する法則）である。

3. モノイド圏

モノイド圏はただ1つの対象を持つ弱2-圏でした。厳密モノイド圏は単対象の厳密2-圏です。直積を入れた集合圏やテンソル積を入れたベクトル空間の圏は非厳密2-圏です。

• 対象は、0（なんでもいい）である。
• 射は、モノイド圏の対象である。
• 2-射は、モノイド圏の射である。
• 射の横結合は、モノイド圏の対象のモノイド積である。
• 2-射の縦結合は、モノイド圏の射の結合である。
• 2-射の横結合は、モノイド圏の射のモノイド積である。

4. 2-離散な2-圏

任意の圏Cに対して、恒等2-射だけを持つ2-離散な厳密2-圏を作れます。こうしてCから作った厳密2-圏をC⁽²⁾と書くことにします。

• 対象は、Cの対象である。
• 射は、Cの射である。
• 2-射は、Cの射 f:X→Y ごとの id_f::f⇒f:X→Y である。（その他の2-射はない。）
• 射の横結合は、Cの射の結合である。
• 2-射の縦結合は、恒等2-射の自明な結合である。（特に考える必要はない。）
• 2-射の横結合は、if_f;id_g = id_f;g で与えられる。

5. 順序半環係数の行列の圏

K = (K, +, 0, ・, 1, ≦) が順序半環のとき、K係数（Kを成分とする）行列の圏は厳密2-圏の構造を持ちます。K = N（自然数に、常識的な順序半環構造） とか K = ({true, false}, ∨, false, ∧, true, (true＜false とする順序)) が事例です。より詳しくは「これならいじれるぞ、2-圏の簡単な例」を参照してください。

• 対象は、自然数である。
• 射は、K係数の行列である。
• 2-射は、成分ごとに比較する順序関係である。
• 射の横結合は、行列の積である。
• 2-射の縦結合は、行列のあいだの順序の推移律である。
• 2-射の横結合は、行列の積の順序（に関する法則）である。

6. 関係圏

関係圏Relも順序構造を考慮すると厳密2-圏になります。これは、すぐ上の例である行列の圏で、真偽値半環を係数とした場合の拡張です。同様な拡張は任意の順序半環に対して行えます。「スパンの圏と行列の圏」も参照してください。

• 対象は、集合である。
• 射は、集合のあいだの関係である。
• 2-射は、関係のあいだの包含関係である。
• 射の横結合は、関係の結合である。
• 2-射の縦結合は、関係のあいだの包含関係の推移律である。
• 2-射の横結合は、関係の結合の包含関係（に関する法則）である。

7. アルファベット集合と翻訳の圏

クリーネスターと関係圏を利用して、形式言語理論で使える厳密2-圏を定義できます。

• 対象は、集合（アルファベット集合）である。
• 射は、文字列のあいだの翻訳である。アルファベットX上の文字列からアルファベットY上の文字列への（非決定性で線形な）翻訳は、X→Y^* という非決定性写像とする。ここで、上付きスターはクリーネスター。
• 2-射は、翻訳をクリーネスターのあいだの関係と見ての包含関係である。（非決定性写像は関係とみなせる。）
• 射の横結合は、関係の結合である。
• 2-射の縦結合は、関係のあいだの包含関係の推移律である。
• 2-射の横結合は、関係の結合の包含関係（に関する法則）である。

8. 入出力を持つオートマトンの圏

入出力を持つ非決定性オートマトンは、次のようなモノで構成されます。

1. 入力アルファベット集合X
2. 出力アルファベット集合Y
3. 状態集合S（空ではない）
4. 状態遷移非決定性写像（あるいは遷移関係） δ:X×S→S×Y^*
5. 始状態の集合 I∈S
6. 終状態の集合 F⊆S

入出力を持つオートマトンの全体は、入出力の結合と模倣関係により弱2-圏を構成します。その記述はちょっと長くなるので今回は割愛します。S = {0} と固定すると、すぐ上の例と同じになります。

9. 0次元のコボルディズム圏

微分同相による同値関係で割る前のコボルディズム圏は厳密2-圏になります。幾何的次元（扱う多様体の次元）が高くなると記述が面倒ですが、0次元なら簡単に記述できます。

• 対象は、有限個の点である。
• 射は、n個の始点とm個の終点を境界とするコンパクトでなめらかな1次元有向多様体である。
• 2-射は、なめらかな1次元有向多様体のあいだの境界を固定したなめらかな写像である。微分同相写像に限定する場合が多いが、ここでは任意のなめらかな写像とする。
• 射の横結合は、終点境界と始点境界を貼り合わせることである。
• 2-射の縦結合は、なめらかな写像の結合である。
• 2-射の横結合は、なめらかな写像を貼り合わせることである。

10. 双加群の圏

代数的な例として、双加群（両側加群）の弱2-圏があります。

• 対象は、可換環である。
• 射は、左右のスカラー乗法（作用）を持つ双加群（両側加群）である。
• 2-射は、双加群のあいだの準同型写像（加法と左右のスカラー乗法を保つ線形写像）である。
• 射の横結合は、双加群のテンソル積である。
• 2-射の縦結合は、準同型写像の結合である。
• 2-射の横結合は、準同型写像のテンソル積である。

単対象2-圏からのラックス2-関手

圏の次元が上がると、関連する定義や記述が面倒になってきます。2次元でも既に、関手の構造はけっこう複雑です。以前、ラックス・モノイド関手の説明はしたことがあるので、ラックス・モノイド関手の拡張としてラックス2-関手を定義しましょう。

一般的な弱2-圏をA, Bなどとします。弱2-圏の構成素を表す記号は次のように約束します。

• 対象は、X, Yなどの大文字で表す。
• 射は、f, gなどの小文字で表す。
• f:X→Y のとき、X = left(f), Y = right(f) と表す（dom, codは2-射に関して使うことにする）。
• 2-射は、α, βなどのギリシャ文字で表す。
• α::f⇒g:X→Y のとき、f = dom(α), g = cod(α), X = left(α), Y = right(α) と表す。
• 射の横結合はf*gで表す（f;gではないので注意）。
• 2-射の縦結合はα;βで表す。
• 2-射の横結合はα*βで表す。（射のときと同じ記号を使う。）
• 対象Xに対する単位射はunit_Xで表す（id_Xではない）。unit_Xは横結合*に対する単位（中立元）となる。
• 射fに対する恒等2-射をid_fで表す。id_fは縦結合;に対する恒等（中立元）になる。
• unit_Xのidは、idunit_X と書く。

この約束はこの記事のローカルルールで、記法の選択に特に根拠はありません（けど、なにかしらの約束は必要です）。次元を明示すれば、このような約束は不要ですが、とても煩雑になります。以上の約束により、次のような“みなし”が導入されます。

• 大文字Xは、暗黙に X∈|A|₀ とみなす。
• 小文字fは、暗黙に f∈|A|₁ とみなす。
• ギリシャ文字αは、暗黙に α∈|A|₂ とみなす。
• *は、|A|₁×|A|₁→|A|₁ という部分写像である。
• ;は、|A|₂×|A|₂→|A|₂ という部分写像である。
• *は、|A|₂×|A|₂→|A|₂ という部分写像で、同じ記号がオーバーロードされている。
• unitは、|A|₀→|A|₁ という写像である。
• idは、|A|₁→|A|₂ という写像である。
• idunitは、|A|₀→|A|₂ という写像である。

次元がもっと高くなると、「文字種によって次元を区別する」「次元ごとに別な名前で呼ぶ（例：「単位」と「恒等」）」ような約束は使えなくなります。一般的な表記法のヒントは「高次圏の下部構造を箙〈えびら〉で表現してみる」にあります。

さて、弱2-圏Aの対象が1個だけの場合を考えます。ただ1つの対象をXとします。この場合、ラックス2-関手はラックス・モノイド関手とほとんど同じものです。ラックス・モノイド関手については、次の記事を参照してください。

• モノイド関手／ラックス・モノイド関手とその実例
• ラックス・モノイド関手について、もうちょっと

Aが単対象の弱2-圏（モノイド圏）のとき、AからBへのラックス2-関手は次のモノから構成されます。

1. Bの対象Y
2. Aのホム圏A(X, X)からBのホム圏B(Y, Y)への関手F
3. B(Y, Y)の射（Bの2-射） ε:unit_Y→F(unit_X)
4. ホム圏A(X, X)の2つの対象（Aの射）f, gを添字に持つB(Y, Y)の射（Bの2-射）の族 μ_{f, g}:F(f)*F(g)→F(f*g)

対象がXだけの場合は、弱2-圏Aとそのホム圏A(X, X)は同じものです。それにも関わらず、構成素の次元はズレます。一般に、2つのモノを繋ぐホム構造の次元は下がるので、ホム構造内での構成素の次元も下がります。

弱2-圏の構成素	ホム圏の構成素
対象X	なし
射 f:X→Y	対象 f
2-射 α::f⇒g:X→Y	射 α:f→g

同じfやαの次元が、見方により変わるのです。

• (f:X→Y in A) = (f in A(X, X))
• (α::f⇒g:X→Y in A) = (α:f→g in A(X, X))

以上に説明した (1) Y∈|B|₀, (2) ホム圏のあいだの関手 F:A(X, X)→B(Y, Y), (3) ε::unit_Y⇒F(unit_X):Y→Y in B, (4) μ_f,g::F(f)*F(g)⇒F(f*g):Y→Y in B の組み合わせは、特定の法則を満たすことを要求されます。その法則は、結合律、左単位律、右単位律です。

以下は、結合律と左単位律（右単位律は左と同様）を示すストライプ図です。

テキスト表記と可換図式を使ったラックス2-関手の詳細な記述は、nLabの定義を参照してください。

• https://ncatlab.org/nlab/show/monoidal+functor
• https://ncatlab.org/nlab/show/oplax+monoidal+functor
• https://ncatlab.org/nlab/show/pseudofunctor

いま定義した(Y, F, μ, ε)は、一般的なラックス2-関手ではなくて、単対象2-圏（モノイド圏と同じモノ）からのラックス2-関手です。今回の目的では、単対象2-圏からの関手で十分なので、一般的なラックス2-関手の説明はしません。（必要なら、すぐ上のnLab記事などを参照。）

自明な2-圏

XCat = Lax2(1⁽²⁾, SPAN(Set)) に登場する1⁽²⁾は自明な2-圏です。自明な2-圏は、空な2-圏（何もない）を除けば、2圏のなかで最も簡単なものです。簡単過ぎてかえって分かりにくい存在かも知れません。

1⁽²⁾以外に、自明な0-圏1⁽⁰⁾、自明な1-圏1⁽¹⁾も一緒に説明しましょう。記法を単純にするために：

• I := 1⁽⁰⁾
• J := 1⁽¹⁾
• K := 1⁽²⁾

とします。これから I, J, K について考えます。

Iは単なる集合で、I = {0} とします。Jは通常の圏で、

• 対象：|J|₀ = I = {0}
• 射： |J|₁ = {1}
• dom, cod： dom(1) = cod(1) = 0
• 恒等： id₀ = 1
• 結合： 1;1 = 1

2-圏Kは、1-圏Jに恒等2-射を付け加えて2-離散な2-圏です。具体的に定義しましょう。

• 対象：|K|₀ = I = {0}
• 射： |K|₁ = |J|₁ = {1}
• 射のleft, right: left(1) = right(1) = 0
• 単位： unit₀ = 1
• 射の横結合： 1*1 = 1
• 2-射： |K|₂ = {2}
• left, right: left(2) = right(2) = 0
• dom, cod：dom(2) = cod(2) = 1
• 恒等： id₁ = 2
• 2-射の縦結合： 2;2 = 2
• 2-射の横結合： 2*2 = 2

すべての定義が自明ですが、それでもややこしいところがあります。Kの2-射を捨てて、対象と射を考えると通常の圏（1-圏）になります。その圏をK₁とすると：

• K₁ J

一方、2-圏Kのホム圏K(0, 0)も通常の圏でJと同型な圏です。

• K(0, 0) J

しかし、K₁とK(0, 0)は違う圏です。K₁の構成素は{0, 1}、K(0, 0)の構成素は{1, 2}です。次元が高いほうを捨てて作ったのがK₁で、次元が低いほうを忘れて次元をズラして作ったのがK(0, 0)です。また、ホム圏K(0, 0)には横結合に由来するモノイド積*が入り、モノイド圏となります。結合もモノイド積も実質は同じ演算ですが、K(0, 0)は名目上2つの演算を持つのです。

自明な2-圏からのラックス2-関手

1⁽²⁾は単対象の2-圏なので、1⁽²⁾から弱2-圏Bへのラックス2-関手は次のモノで決まります。

1. Bの対象X
2. ホム圏1⁽²⁾(0, 0)からホム圏B(X, X)への通常の関手
3. F(-)*F(-) から F(-*-) への自然変換 μ::F(-)*F(-)⇒F(-*-):1⁽²⁾(0, 0)×1⁽²⁾(0, 0)→B(X, X)
4. ε:unit_X→F(1) in 1⁽²⁾(0, 0) （ε::unit_X⇒F(1):X→X in B）

結局、横結合をモノイド積とするモノイド1⁽²⁾(0, 0)から、同様に作ったモノイド圏B(X, X)へのラックス・モノイド関手(F, μ, ε)がラックス2-関手となります。モノイド圏としての1⁽²⁾(0, 0)は自明なモノイド圏なので、(F, μ, ε)はモノイド圏B(X, X)内のモノイド(F(1), μ_1,1, ε)と同じことです -- このことは次の記事に書いてあります。

• ラックス・モノイド関手について、もうちょっと / 自明なモノイド圏からのラックス・モノイド関手

「モノイド圏B(X, X)内のモノイド」の別な言い方が、「弱2-圏B内のX上のモナド」です。よって、次の3つの概念は同じです。

1. 自明な2-圏1⁽²⁾から弱2-圏Bへのラックス2-関手
2. 弱2-圏Bのホム・モノイド圏B(X, X)内のモノイド
3. 弱2-圏B内のX上のモナド

特に、B = Cat とした場合が、通常のモナドとなります。

弱2-圏BipartQuiv内のモナドは圏

いよいよ（やっと）、圏（小さい圏）の別定義を述べることができます。我々の代替圏論における圏とは、二部箙の弱2-圏BipartQuiv内のモナドです。BipartQuivの対象Xを選ぶと、X上のモナドは、ホム・モノイド圏BipartQuiv(X, X)内のモノイドです。このモノイドの構成素は次のモノです。モノイド圏BipartQuiv(X, X)のモノイド積（ファイバー積）をで表します。

1. 集合X
2. 二部箙 A = (X, X, A, src_A, trg_A)
3. 二部箙の準同型写像 μ:AA→A
4. 二部箙の準同型写像 ε:unit_X→A

二部箙と書いてますが、始頂点集合と終頂点集合が一致しているので、Aは通常の箙（有向グラフ）で、Xがその頂点集合です。BipartQuiv(X, X)の射は箙の準同型なので、(A, μ, ε)は箙を台とするモノイドになります。

箙（有向グラフ）を台とするモノイドと言えば圏であることはお馴染みでしょうが、次の点に注意して確認してください。

• AAは {(f, g)∈A×A | trg(f) = src(g)} と書ける。
• x, y∈X に対して、A(x, y) = {f∈A | src(f) = x かつ trg(f) = y} とすると、(AA)(x, z) = Σ(y∈X | A(x, y)×A(y, z)) と書ける。
• 従ってμは、μ[x, y, z]:A(x, y)×A(y, z)→A(x, z)により記述できる。
• ε: unit_X→A は、単なる写像 X→A（このAは箙のアロー集合）と同じである。

箙 A = (X, A, src_A, trg_A) に、箙の準同型写像 μ:AA→A, ε:unit_X→A がある状況で、満たすべき法則は結合法則、左単位法則、右単位法則で、それは次の形に書けます。ただし、弱2-圏の結合律子（associator）と左右の単位律子（unitor）は省略しています（律子（りつし）に関しては「律子からカタストロフへ」を参照してください）。

• (μ[x, y, z]×id_{A(z, w)});μ[x, z, w] = (id_{A(x, y)}×μ[y, z, w]);μ[x, y, w] : A(x, y)×A(y, z)×A(z, w)→A(x, w)
• (ε(x)×id_{A(x, y)});μ[x, x, y] = id_{A(x, y)} : A(x, y)→A(x, y)
• (id_{A(x, y)}×ε(y));μ[x, y, y] = id_{A(x, y)} : A(x, y)→A(x, y)

左斜め加群と右斜め加群

圏を弱2-圏BinpartQuiv内のモナドとして定式化しました。この方法のメリットは、通常のモナドと圏に共通の定義を与え、お互いの理論が行き来する通路を与えることです。もうひとつのメリットは、圏のあいだの準同型写像が一般化されることです。モナドのあいだの準同型写像が、通常の関手よりずっと広い概念だからです。

一般的なモナドとは、自明な2圏1⁽²⁾から弱2-圏（厳密2-圏も含む）Bへのラックス2-関手なので、モナドの準同型はラックス2-自然変換だと考えるのが自然でしょう。ラックス2-自然変換の、より分かりやすい（と思える）定式化として、ここでは斜め加群（oblique module）という概念を紹介します。概念に新しいものはありませんが、「斜め加群」という言葉は僕の造語です。

Bが弱2-圏で、(X, M, μ, ε)がB内の（X上の）モナドとします。（Mは大文字ですが、ここではBの射を表します。）念のため繰り返すと、モナドの構成素は：

1. Bの対象X
2. Bの射 M:X→X
3. Bの2-射 μ::M*M⇒M:X→X （*はBの横結合）
4. Bの2-射 ε::unit_X⇒M:X→X （unit_XはBの単位射）

ホム圏B(X, X)の言葉で言えば：

1. B(X, X)の対象M
2. B(X, X)の射 μ::M*M→M （*はB(X, X)のモノイド積）
3. B(X, X)の射 ε::unit_X→M （unit_XはB(X, X)の単位対象）

満たすべき法則は、結合律、左単位律、右単位律です。

M = (X, M, μ, ε), N = (Y, N, ν, ι) がB内の2つのモナドのとき、左(M, N)-斜め加群は次のモノから構成されます。

• Bの射 F:X→Y
• Bの2-射 α::M*F⇒F*N:X→Y

左(M, N)-斜め加群(F, α)が満たすべき法則はモナド乗法とモナド単位の擦り抜け法則です。これらの法則をストリング図で表せば次のようになります。

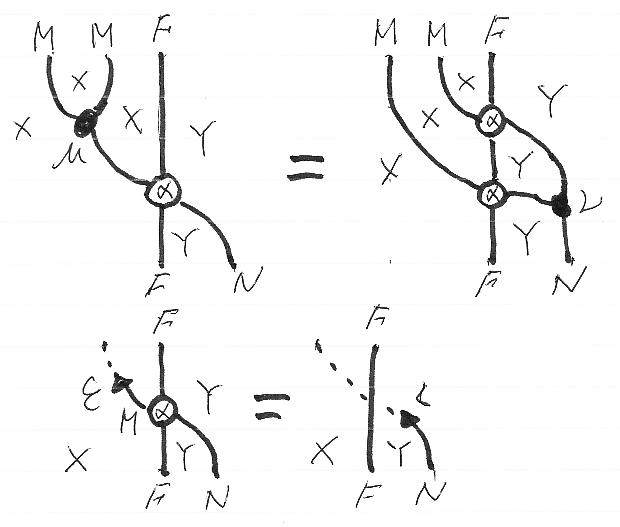
右(M, N)-斜め加群(F, β)も同様に定義されます。

• Bの射 F:X→Y
• Bの2-射 β::F*N⇒M*F:X→Y

左(M, N)-斜め加群を使っても右(M, N)-斜め加群を使っても同じことですが、ここでは左斜め加群を使うことにします。ラックス2-自然変換の定義として右斜め加群を採用していることもある（多数派かも）ので注意してください。

左斜め加群の圏

前節に引き続き、Bは弱2-圏（Bは厳密2-圏でもよい）だとします。M = (X, M, μ, ε), N = (Y, N, ν, ι) をB内の2つのモナドとします。言い方を換えると、MはB(X, X)内のモノイド、NはB(Y, Y)内のモノイドです。左(M, N)-斜め加群の全体をLeftOblMod_B(M, N)と書くことにします。下付きのBは省略することがあります。

(F, α), (G, β)∈LeftOblMod_B(M, N) のとき、(F, α)から(G, β)への左斜め加群の準同型とは次のモノです。

• 弱2-圏Bの2-射 φ::F⇒G:X→Y
• φは、α;(φ*N) = (M*φ);β を満たす。

満たすべき法則をストリング図で描けば次のようです。

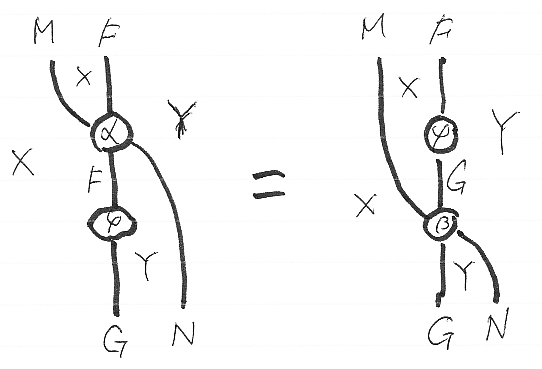
Y上のモナドNが、N = (Y, unit_Y, unit_Y*unit_Y⇒unit_Y, idunit_Y) という自明なモナドの場合、左斜め加群は左加群（モナドによる左作用）とみなせ、左斜め加群の準同型は左加群の準同型と同じ概念になります。

この節の最初で、LeftOblMod_B(M, N)を左(M, N)-斜め加群全体の集合（類）としましたが、ホムセットを定義して、LeftOblMod_B(M, N)を圏とみなすことができます。

• 対象： |LeftOblMod_B(M, N)| = (左(M, N)-斜め加群の全体)
• ホムセット： (LeftOblMod_B(M, N))((F, α), (G, β)) = ((F, α)から(G, β)への左斜め加群の準同型の全体)
• 射の結合： Bの2-射としての縦結合
• 恒等射： Bの恒等2-射

ラックス2-関手の2-圏

代替圏論における“圏の圏”は、次のように定義されるのでした。

• XCat = Lax2(1⁽²⁾, SPAN(Set))

通常の“圏の圏”Catは2-圏（厳密2-圏）なので、XCatも2-圏の構造を持つべきです。となると、右辺Lax2(1⁽²⁾, SPAN(Set))に2-圏の構造が必要です。

ラックス2-関手の全体に対して、次のような構成素により2-圏構造を入れることができます。

• 対象は、ラックス2-関手
• 射は、ラックス2-関手のあいだのラックス2-自然変換
• 2-射は、ラックス2-自然変換のあいだの変更手（modification）

変更手は2-自然変換のあいだの変換です。一般に、n-自然k-変換という概念があり、ラックス2-関手は（ラックスな）2-自然0-変換、2-自然変換は2-自然1-変換、変更手は2-自然2-変換です。こらについては次を参照してください。

• https://ncatlab.org/nlab/show/lax+natural+transformation
• https://ncatlab.org/nlab/show/modification
• https://ncatlab.org/nlab/show/transfor

幸いに、自明な2-圏からのラックス2-関手の場合は、n-自然k-変換（高次変換）の理論を持ち出さなくても、ラックス2-関手の2-圏を記述できます*6。

高次変換の概念	代数的概念
ラックス2-関手	モナド
ラックス2-自然変換	左斜め加群
変更手	左斜め加群の準同型

弱2-圏Bに対して、Lax2(1⁽²⁾, B)をMonad_Bと略記すると。Monad_Bは2-圏であり、次の構成素からなります。

• |Monad_B|₀ = (B内のモナドの全体)
• |Monad_B|₁ = (B内の左斜め加群の全体)
• |Monad_B|₂ = (B内の左斜め加群準同型の全体)

2-圏Monad_Bのホム圏は、

• Monad_B(M, N) = LeftOblMod_B(M, N)

M, N, Lが3つのモナドで、(F, α):M→N in Monad_B, (G, β):N→L in Monad_B のとき、(F, α)と(G, β)の横結合は、αとβのBにおける横結合で与えられます。

• (F, α)*(G, β) = α*β = (α*G);(F*β)

左斜め加群の準同型の横結合も、Bの横結合として定義できます。

まとめと展望

長々と説明してきましたが、“高次でラックスな圏と変換の理論”の特殊ケースを取り上げただけです。

• A, B が弱2-圏のとき、「ラックス2-関手、ラックス2-自然変換、変更手」から構成される2-圏Lax2(A, B)を構成できる。
• 特に、A = 1⁽²⁾ のとき、Lax2(1⁽²⁾, B)はB内のモナドの2-圏となる。
• Monad_B = Lax2(1⁽²⁾, B) に対しては、「モナド、左斜め加群、左斜め加群の準同型」という代数的な記述が可能である。

さらにBを特定の2-圏にすると：

• Monad := Monad_Cat
• XCat := Monad_BipartQuiv

2-圏XCatの理論が代替圏論です。代替圏は通常のモナドと明らかな類似性があります。ただし今回は、通常の「圏、関手、自然変換」の2-圏Catと代替圏の2-圏XCatとの関係にあまり言及してません。CatをXCatに埋め込めますが、埋め込み方が自明とも言えません。[追記]埋め込めるかな？ Catを素直に埋め込みのためには、XCatの定義を変えたほうがいいかも知れません。「弱2-圏内のモナドに関する補足：モナドが作る2-圏の多様性」を参照。[/追記]

枠組は出来たので、ベックの分配法則を代替圏に適用することが次の目標になるでしょう。また、Cat, BipartQuiv（SPAN(Set)）以外の2-圏Bに対する Monad_B = Lax2(1⁽²⁾, B) を作ってみるのも面白そうです。

*1:終対象とファイバー積を持つことは、終対象と直積と等値核（イコライザー）を持つと言っても同じです。また、有限完備とか「有限極限を持つ」とも言い換えられます。

*2:ラックの論文"Composing PROPs"では、ベックの分配法則を使っています。

*3:これは圏論に限ったことじゃないですけどね。例えば、型理論の用語法も酷いもんです。→「型推論に関わる論理の概念と用語 その2」

*4:カレン語だと「言葉がきまじっちゃってるのが、やわらがります。」

*5:[追記]n = 2 の場合が特殊というより、n = 2, 3 あたりを扱う低次元圏論と、一般の次元を扱う一般高次圏論に違いがある、というのが実情ですね。「高次圏： 用語法と文脈（主に2次元） // 文脈により言葉の解釈が変わる」を見てください。[/追記]

*6:僕は、高次変換（transfor, higher transformation）の理論を理解してません。