2013年に「絵算したい人のためにオススメする3つのストリング図解説 (とオマケ)」という記事を書きました。絵算(お絵描き計算、pictorial/graphical/diagrammatic calculation)は、圏論の理解や計算を、図式を使って行う方法です。使用される図式をストリング図(string diagram)と呼びます。
最近、ストリング図の良い解説を見つけました。ダニエル・マースデン(Daniel Marsden)の次の論文です。
- Title: Category Theory Using String Diagrams
- Author: Daniel Marsden
- URL: http://arxiv.org/abs/1401.7220
- Pages: 60p.
2014年発表なので、以前の記事のときには存在してなかったものです。この論文を紹介しながら、絵算に関する“よしなしごと”を記します。
[追記]絵算をやってみたい人は、知識の習得だけでなく、双対や随伴に強くなるためのトレーニングを必ずしましょう。[/追記]
内容:
ストリング図は流派が乱立
ストリング図の利用はポピュラーになってきましたが、その描き方がキチンと決まっているわけではありません。人により描き方はまちまちです。「絵算(ストリング図)における池袋駅問題の真相」で、代表的な絵算使い9人(7人+1組)の描き方を紹介しています。射の結合とテンソル積(モノイド積)をどの方向に描くかを表にまとめたものが次です。絵のサンプルは「池袋駅問題の真相」記事にあります。
| 人名 | 図:射の結合 | 図:テンソル積 | テキスト:射の結合 | テキスト:テンソル積 | まとめると |
|---|---|---|---|---|---|
| キュリア | 上から下↓ | 左から右→ | 右から左← | 右から左← | ↓→←← |
| メリス | 下から上↑ | 左から右→ | 右から左← | 左から右→ | ↑→←→ |
| ストリート | 下から上↑ | 左から右→ | 右から左← | 左から右→ | ↑→←→ |
| ウィラートン | 下から上↑ | 右から左← | 右から左← | 右から左← | ↑←←← |
| セリンガー | 左から右→ | 下から上↑ | 右から左← | 左から右→ | →↑←→ |
| 長谷川 | 左から右→ | 下から上↑ | 右から左← | 左から右→ | →↑←→ |
| クック | 下から上↑ | 左から右→ | 右から左← | 左から右→ | ↑→←→ |
| バエ/ステ | 上から下↓ | 左から右→ | 右から左← | 左から右→ | ↓→←→ |
メリスとストリート、セリンガーと長谷川が同じですが、他はバラバラです。マースデン(Daniel Marsden)はメリス/ストリートと同じなので、「↑→←→」方向が多数派になりましたね。([追記]クックも同じ「↑→←→」でした。[/追記])
ストリング図は、トレース付きモノイド圏、コンパクト閉圏、デカルト閉圏などの計算でよく使われますが、ここでは「圏、関手、自然変換」の計算にストリング図を使う場合を扱います。「圏、関手、自然変換」をセルと呼び、それぞれ、0次元セル、1次元セル、2次元セルといいます。n次元(n = 0, 1, 2)セルを絵に描くときは、(2 - n)次元の図形を使います。n←→(2 - n) の対応はポアンカレ双対と呼ばれます。
| セル | セルの次元 | 双対次元 | 図示すると |
|---|---|---|---|
| 圏 | 0 | 2 | 面、領域、エリア |
| 関手 | 1 | 1 | 線、エッジ、ワイヤー |
| 自然変換 | 2 | 0 | 点、ノード、ドット、ボックス、オダンゴ |
オダンゴとは、0次元図形を大きさを持つ円や楕円により描いたものです。キュリア、メリス、ストリート、ウィラートン、バエズ、ステイはオダンゴを使っています。セリンガー、長谷川、クックはボックスを使っており、今回新しく紹介するマースデンだけが2次元セル=0次元図形にドットを使っています。ただし、セルの形は同じ人でも状況により変えることもあります。
キュリアとマースデン
「圏、関手、自然変換」のストリング図に関する詳しい説明として、キュリアによる次のテキストがあります。
- Title: Category theory: a programming language-oriented introduction
- Author: Pierre-Louis Curien
- URL: http://www.pps.univ-paris-diderot.fr/~mellies/mpri/mpri-ens/articles/curien-category-theory.pdf
- Pages: 145p.
第2章"String Diagrams"(第2章の分量:56ページ)がストリング図の説明です。僕は、キュリアのテキストから多くを学んだので、マースデンの新しいテキストとキュリアのテキストを比較しながら話します。
まず、自然変換の交替律(interchange law、キュリアはエレベーター規則とも呼んでいる)を見てみましょう。
[キュリア p.32]
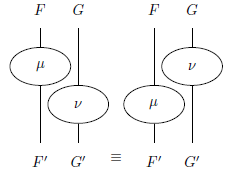
[マースデン p.7]
キュリアとマースデンでは、上下の方向が逆転しています。キュリアの左端は μ::F⇒F' と上から下に読み、マースデンの左端は α::F⇒F' と下から上に読みます。
オダンゴとドットの違いもありますが、より目立つ違いはマースデンが色を使っていることです。マースデンは一貫して色を使っており、見た目がきれいでスッキリとした絵になっています。
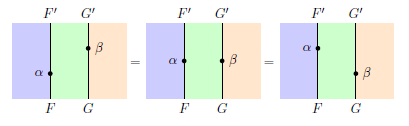
別な例として、随伴や双対を表現するニョロニョロ関係(snake relation、「双対とニョロニョロ」参照)は次のようです。
[キュリア p.34]
[マースデン p.10]

キュリアのはオダンゴが大きすぎて邪魔くさいですね。マースデンのほうがずっと見やすい。ただ、マースデンは、ワイヤーのラベル(関手の名前)を枠の外にだけ書くようにしているらしく、無名のワイヤーの意味が取りにくいことがあります。一番左の絵で言えば、ηとεを繋ぐワイヤーはGなのですが、それが明示されていません。
ラベルの付け方も人により違うので表にしておきます。キュリア、マースデン以外にウィラートンも入れました。
| 人名 | エリアのラベル | ワイヤーのラベル | ノードのラベル |
|---|---|---|---|
| キュリア | なし | ワイヤーのそば | オダンゴのなか |
| マースデン | 色 | 枠の外 | ドットのそば |
| ウィラートン | エリアのなか | ワイヤーのそば | オダンゴのなか |
キュリアはエリアのラベル(圏の名前)を省略しており、色も使ってないので、本文を読まないと解釈に悩むことがあります。エリアのラベルを書き込むとうるさくはなるのですが、必要に応じて記入したほうがいいと思います。描き方の原則に拘るよりは分かりやすくするべきでしょう。
絵算のテクニック:格上げ
キュリアとマースデンが説明している絵算のテクニックには次のようなものがあります。
- 格上げ
- 明示的な等号ノード
- 関手ボックス(functor box, functorial box)
- ホム関手の図示
格上げは最も重要なテクニックでしょう。このブログ内でも何度か触れています。
格上げとは、圏の対象を関手とみなし、圏の射を自然変換とみなす方法です。マースデン論説の最初のほう(2.1 Some Elementary Techniques)で説明されています。
[マースデン p.8]

f:X→Y in C を、f::X⇒Y:1→C と再解釈します。ここで1は、単一対象とその恒等射だけからなる自明な圏です。マースデンはこの自明な圏にクリーム色を固定的に割り当てています。
キュリアはエリアのラベル=圏の名前を省略するので、格上げされている事実が分かりにくいことがあります。余談ですが、最近僕は自明な圏を☆でマークしています。以前は1と書いていたのですが、1(イチ)やI(アイ)は色々な意味で使われすぎて紛らわしいことに気が付いたからです。
1, Iが使われる例:
- 数値のイチ
- モノイドや環の単位元
- 単元集合
- 圏の終対象
- 圏の恒等射
- モノイド圏の単位対象
- 自明な圏(単位圏)
- 恒等関手
- 恒等自然変換
対象→関手、射→自然変換 という格上げの特別な例として、集合とその要素も、関手と自然変換と同列に扱います。
[マースデン p.8]

これは、x∈X の絵です。マースデンにならって単元集合を*(アスタリスク)で書くことにします。集合Xの要素xは、*→X という写像と同一視できます。したがって、x:*→X in Set。単元集合*と集合Xは自明圏☆から集合圏Setへの関手とみなせます。x:*→X を、x::*⇒X:☆→Set と格上げして考えるのです。これにより、集合の要素と自然変換を混ぜた計算が出来るよになります。
自明圏と同様に、集合圏Setもまた頻繁に使用する具体的な圏なので、マースデンはSetにピンク色を割り当てています。
絵算のテクニック もっと:等号ノード、関手ボックス
明示的な等号ノード(explicit equality nodes)はキュリアが導入した手法で、マースデンは使っていません。テキストとして書く等式の情報を、絵のなかに取り込む方法です。
簡単な例として次の絵を見てみましょう。(これは、https://hal.archives-ouvertes.fr/file/index/docid/697115/filename/csl-2008.pdf のp.9から)

H = F;G (反図式順記法なら H = GF、DOTN二号なら H = F*G)というテキストで書いた等式があるとします。そうすると、Hの恒等自然変換 H⇒H と F;Gの恒等自然変換 F;G⇒F;G は同じものです。この恒等自然変換をι(イオタ)と書くと、ι::H⇒F;G と書けます。図の上のほうのオダンゴはιのことです。一方、ι:F;G⇒H とも書けて、図の下のオダンゴがこっちのιを表しています。
明示的な等号ノードを使うと、本文側に書いてあるテキスト等式を参照しなくても済むようになります。絵だけで完結できるのです。また、テキストによる等式的推論を絵の変形で代行することも(ある程度は)出来ます。
関手ボックスは、キュリアもマースデンも使っています。g = F(f:X→Y) のような情報を絵で表すためのものです。どうやら次の論文が起源のようです。
- Title: Linearly distributive functors (1999)
- Authors: J. R. B. Cockett and R. A. G. Seely
- URL: http://www.chimaira.org/archive/LinearlyDistributiveFunctors_linmorph.ps.pdf
関手ボックスの詳しい説明はメリスの論文がおすすめです(絵がきれい)。
- Title: Functorial boxes in string diagrams
- Author: Paul-Andre Mellies
- URL: http://www.pps.univ-paris-diderot.fr/~mellies/papers/functorial-boxes.pdf
ホム関手の図示は、キュリアが考えた手法のようです。マースデンは使ってません。一種の格上げですが、今回は割愛します。
テキスト記法の問題点
絵のなかでのセル(射、関手、自然変換)の結合方向とテキストにおけるセルの結合方向が違うと、その違いをいちいち脳内変換しなくてはならず負担になります。絵とテキストの方向を合わせると、とてもスッキリします。にもかかわらず、先に紹介した9人のなかで絵とテキストの方向を合わせているのはウィラートンだけです。ウィラートンは絵を右から左に描いているのです。
どうしてテキストを左から右にしないのでしょうか? テキスト記法を変更するのが一番自然だと思うのですがね、右から左という不自然な逆方向になんで拘るの? そんなわけで、左から右への記法については何度も述べています。
左から右に書く記法(DOTN二号)の概略は次のようです。
| 意味 | 多数派の記法 | DOTN二号 |
|---|---|---|
| 射の結合 | g |
f;g |
| 関手の結合 | G |
F*G |
| 自然変換の縦結合 | β |
α;β |
| 自然変換の横結合 | α*β, α |
α*β |
| 関手の適用 | F(X) | X.F |
| 自然変換の成分 | αX | X.α |
例を挙げてみましょうか。T = (T, μ, η) が圏C上のモナドで、F:C→C が自然変換λと共にモナド準同型*1となる関手とします。このとき、対象Aを台とするT-代数(アイレンベルグ/ムーア圏の対象)をFにより移した先 A.F (普通の記法ではF(A))もT-代数になります。A.Fの単位律をキュリアは次のように描いています。
[キュリア p.112]

一番左のエリアは自明圏☆で、その他のエリアは圏Cです。AはCの対象、αはCの射ですが、格上げにより A, F, Tが関手、η、λ, α は自然変換とみなします。この絵のイコールの左側を、上段(A, F, η)、中段(A, λ)、下段(α, F)に分けて、格段ごとに左から右に見てテキスト化すると:
- A.F.η ((A.F).η のこと)
- A.λ
- α*F
それぞれの段を縦に結合する演算子記号はセミコロンなので、左辺は (A.F.η);(A.λ);(α*F)、右辺は A.F で、全体として次の等式となります。
- (A.F.η);(A.λ);(α*F) = A.F
格上げしてあったαを射に戻して、右辺のAはAの恒等射(A^と書く)に直すという調整を施して:
- (A.F.η);(A.λ);(α.F) = A^.F
細かい調整を除けば、見たままをテキストに写し取っている感じです。
一方で、多数派である反図式順記法で絵を翻訳すると次のようになります。
- (α*F)
λA
ηF(A) = F(A)
調整を加えた形は:
- F(α)
λA
ηF(A) = F(idA)
並び順は逆だし、下付き添字と丸括弧が混じってデコボコで、なんだか絵と離れている印象ですよね。絵でスラスラ計算できても、テキストとの相互変換に手間がかかるのは嬉しくないなー、と僕は思うのですがいかがでしょう。
ちなみに、今出したキュリアの絵と同じ内容であるマースデンの絵は次です。若干一般化してあって、F:C→C' で、異なる圏上のモナドのあいだの準同型です。
[マースデン p.30]
マースデンの r∈G(X) の図示
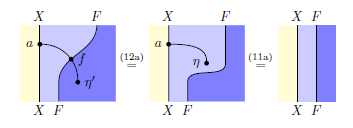
Gが圏Cから集合圏Setへの関手のとき、r∈G(X) をマースデンは次のように図示しています。
[マースデン p.37]
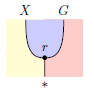
最初見たとき、なんでこう描くのか戸惑ったので説明を加えます。明示的な等号ノードを使うとハッキリします。☆は自明圏、X.G は G(X) の図式順記法です。

マースデンの絵は下から上に見ていくので、まずは下のほう。集合X.G(普通の書き方ではG(X))の要素がrなので、r:*→X.G とみなします。*とX.Gが対象(集合)から関手に格上げされて、rは射から自然変換へと格上げされています。つまり、*:☆→Set、X.G:☆→Set、r::*⇒X.G:☆→Set。
次に等号ノードを見ると、X.Gという関手(格上げで解釈)は、XとGをこの順で結合した関手に等しいことを表しています。明示的な等号ノードは、その名のとおり、明示的に書きたいときに使いますが、不要なら省略可能です。省略した形がマースデンの絵です。
絵算のススメ
絵算は万能ではありませんが、モナド、ベックの分配法則、テンソル強度などが絡んだ計算では絶大な威力を発揮します。
もちろん、トレース付きモノイド圏/コンパクト閉圏/デカルト閉圏の内部での計算でも有効に機能します。
最後に、最近見た壮絶な絵算(サーフェイス図による証明)の例:
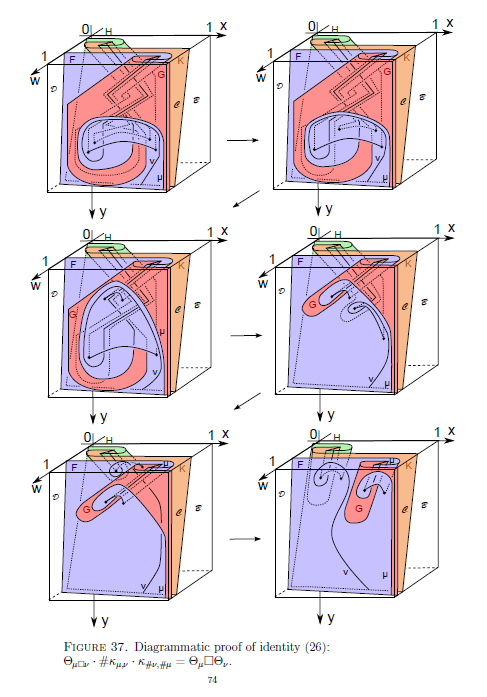
この絵は、次の論文から取ったものです。こういった絵が山のように載っています。こりゃ、ついてけない。
- Gray categories with duals and their diagrams
- John W. Barrett, Catherine Meusburger, Gregor Schaumann
- URL: http://arxiv.org/abs/1211.0529