「第3歩」と書いたからと言って続くかどうかはわからない。だけど、3回書けば既に続きものだとも言えるので、第1歩をハブエントリー(目次ページ)にしておきました。第1歩からリンクをたどれます。
さーて第3歩だけど、そろそろ関手ですかね? いやっ、まーだ実例。もっともっと実例。なんで僕が実例にこだわるかというと、抽象論は好きだけど、具体性のない抽象論が嫌いだから。圏論に関する具体例は山盛りあるんだけど、どうも(良い意味での)アブストラクト・ノンセンスな論法のほうに注目が集まりがちで、そこいらに転がっている具体例が強調されてない気がする。
実際のところ、圏の定義はすごく一般的だから、その例は死ぬほどイッパイあるんだよね。だから、具体例を拾っているときりがない、ってのも確か。なんだけど、手近にあって個性的で面白い圏は紹介しておきたいんです。で、今回は“エッジが効いた”(って、実は意味ワカラン)圏達の登場。
内容:
射がidしかない離散圏
まずは実例から。圏Dを次のように定義します。([追記]アンレー、ガンマがワイに見えるな、フォントによりけりなんだろうが。[/追記])
- 対象の集合: Obj(D) = |D| = {a, b, c}
- 射の集合: D = {α, β, γ} (圏の名前と射の集合は、同じ記号で表す)
- 域: dom(α) = a, dom(β) = b, dom(γ) = c
- 余域: cod(α) = a, cod(β) = b, cod(γ) = c
- 恒等射: ida = α, idb = β, idc = γ
- 結合: α;α = α, β;β = β, γ;γ = γ
対象が3つ、射が3つ。射は、idx(x = a, b, c)の形をしたものに限られます。対象xに対して恒等射idxは絶対に存在するので、圏Dの射を減らそうと思っても無理。つまり、圏Dは「最低限の射しか持たない」圏です。
一般に、任意の集合Xから出発して、x∈Xに対して idx の形の射を一緒に考えると圏ができます。このようにして作られる圏を離散圏(discrete category)と呼びます。離散圏は、対象の集合Xが与えられれば自動的に作れますね。
離散圏は、対象の集合と事実上同じものですから、つまらない圏とみなされがちですが …… つまらない圏っすね。
対象が1つしかないモノイド(as 圏)
射をできるだけ少なくすると離散圏になります。では、対象をできるだけ少なくするとどんな圏になるでしょう。対象が1個もないと射も存在できません。対象も射もない、なにもない圏は空圏(empty category)と呼びますが、空圏は非常につまらない(trivial)です。
んじゃ、対象を1個だけに限りましょう。Mが圏だとして、|M|={★}とします。星印を使ったことに特に意味はなくて、「なんでもいいからなにか1つ」のモノがMの対象なのです。対象が1つしかないので、どんな射も、f:★→★ の形をしています。別な言い方をすると、M = M(★, ★) ですね(矢印の記法やホムセットは前回述べましたよ)。念のため、圏Mをはっきりと定義しておきます。
- 対象の集合: Obj(M) = |M| = {★}
- 射の集合: 特に制限はない。任意の集合でよい。
- 域: 射fが何であっても dom(f) = ★
- 余域: 射fが何であっても cod(f) = ★
- 恒等射: id★ = u (uは選ばれた特別な射)
- 結合: f, gが何であっても cod(f) = dom(g) だから、結合は常に定義可能。
対象が1個しかないと、dom, cod, idは決まり切った構造しか持たないので、射の集合M(圏の名前と射の集合は同じ名称/記号を使います)に注目すると:
- f, g∈M に対して、条件なしに常に f;g が定義できる。
- (f;g);h = f;(g;h) -- 結合法則
- u;f = f;u = f (uはid★)-- 単位法則
上に述べたような、二項演算「;」と単位元uを備えた集合はモノイドと呼びます。んで結局、対象が1つしかない圏は事情上モノイドである、ってことになります。
自然数の全体N = {0, 1, 2, ...}に足し算+と単位元0を一緒に考えるとモノイドになります。対象集合{★}と決まり切ったdom, cod, idを添えると、({★}, N, dom, cod, id, +)は圏になります。要するに、モノイドがあれば、それは対象が1個の圏だとみなせるし、対象が1個の圏はモノイドとみなせるってことです。
圏が与えられると、そこにモノイドを見いだすのは簡単です。圏CのホムセットC(a, a)はモノイドになるからです。例えば、しりとりの圏なら、「し」から始まり「し」で終わるひらがな文字列だけを考えると、これは"し"を単位元とするモノイドです。行列の圏なら、Mat(1, 1), Mat(2, 2), Mat(3, 3)などが、“行列の掛け算”と“各サイズごとの単位行列”に関してモノイドになっています。
射が少ないやせた圏
離散圏は射が最小限しかなくて、いわば「射の砂漠」状態。では、離散圏よりはましだが、射が少ない圏として、次の条件を満たす圏Tを考えましょう。
- どんな対象a, bに対しても、ホムセットT(a, b)はたかだか1個しか射を持たない。
「射がたかだか1個」とは、言い換えると次のことです。
- T(a, b)は空(射がまったくない)であるか、T(a, b) = {f} となる。
この条件を満たす圏をやせた圏(thin category)と呼びます。対象間を結ぶ射がせいぜい1本なので、なんかスジだけのガリガリ、たしかにやせ細ってますな。
次はやせた圏の例を図示したものです。
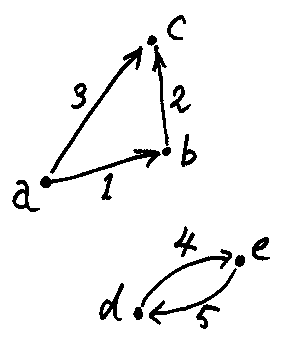
構成要素を列挙してみると:
- 対象の集合: Obj(T) = |T| = {a, b, c, d, e}
- 射の集合: T = {ida, idb, idc, idd, ide, f1, f2, f3, f4, f5}
- 域: 図のとおり
- 余域: 図のとおり
- 恒等射: 自明
- 結合: f1;f2 = f3, f4;f5 = idd, f5;f4 = ide
やせた圏とプレ順序
空集合を0で表すことにします。Tがやせた圏だとして、圏Tの対象集合|T|をAとも呼びましょう。a, b∈Aに対して、T(a, b) ≠ 0のとき(そのときに限って) a≦b と書くことにします。「なんで不等号が出てくるんだ?」と思うでしょうが、まーまー、事情はすぐに明らかになります。とにかく:
- a≦b ⇔ T(a, b)≠0
まず、T(a, a)のなかにはida(だけ)が存在するので、aが何であってもT(a, a)≠0ですね。よって、
- a≦a
次に、T(a, b)≠0、T(b, c)≠0だとしましょう。空でないってことは、ただ1つだけの射が存在するので、T(a, b) = {f}, T(b, c) = {g} と書けます。結合した射 f;g はT(a, c)に入る(dom(f;g) = a, cod(f;g) = cですから)ので、T(a, c) = {f;g}。もちろん、T(a, c)≠0。これから、
- a≦b, b≦c ならば a≦c
「a≦a」と「a≦b, b≦c ならば a≦c」を満たす関係「≦」を備えた集合はプレ順序集合(pre-ordered set)*1と呼びます。つまり、やせた圏の対象集合はプレ順序集合となるわけ。逆に、プレ順序集合が与えられれば、自動的にやせた圏を作れます。
やせた圏Tがさらに次の条件を満たすとき、とてもやせた圏(very thin category)と呼ぶことにしましょう。
- a≠b、T(a, b)≠0 ならば、T(b, a) = 0
とてもやせた圏では、射の一方通行しか許さないのです。とてもやせた圏なら次が示せます。
- a≦b, b≦a ならば、a = b
結論だけ言えば、とてもやせた圏は順序集合とみなせるのです。
それでわかったこと
離散圏、対象が1つの圏、やせた圏は、圏の世界では極地ともいえる辺境に棲む部族達です。実際のところ、これらはそれぞれ、単なる集合、モノイド、プレ順序集合とみなせるので、圏論ではなくて他の分野で扱うべきものです。しかし、ともかくも定義上は、圏の仲間に入るのです。
このことから、圏の定義が非常に一般的/包括的なことは感じ取れるでしょう。あまりに包括的なので、茫漠とした印象もあるのですが、実際に相手にすべきは、実在性と個性を持った(例えばしりとりや行列のような)具体的な個々の圏達です。計算科学の範囲に限っても、オートマトンの圏、データ型(データ領域)の圏、プロセスの圏、ゲームの圏、計算可能関数の圏、回路の圏、仕様の圏、などなど、多様な圏達がそこに蠢〈うごめ〉いています。
*1:前順序集合と呼ぶのが普通ですが、口頭では全順序集合と区別がつかないので「プレ」にしました。