関数の平均・偏差-分解と交代化・歪対称性 - 檜山正幸のキマイラ飼育記 (はてなBlog)

とある説明に「交代化する」とか「‥‥は歪対称である」とかの言い回しが出てきたのですが、その意味がハッキリしませんでした。交代化はある種の平均を求める操作、歪対称性は（平均からの）偏差がゼロである事として特徴付けできそうです。やってみます。

内容：

記号の約束
軌道平均と同変性
射影としての平均化作用素
p次対称群と符号のとき
切断上の関数の拡張

記号の約束

X, Y などは有限集合を表すとします。Gは有限群です。群の演算は特に演算子記号を用意せずに併置で書きます； σ, τ∈G に対して στ∈G のように。群Gの単位元は e とします。

Rは、有理数体Qを含む可換環（同じことですが、Q上の可換代数〈可換多元環〉）とします。Rのなかで、整数 n（n ≠ 0）による割り算ができます。Rが体であることは仮定しませんが、R = Q とか R = R と思ってもかまいません。以下、Rをひとつ選んで固定します。

Map(X, R) は、有限集合Xから可換環Rへの写像全体からなる集合です。単なる集合ではなくて、足し算とRによる掛け算を考えて、Map(X, R) はR-加群とみなします。R = Q、R = R の場合なら、Map(X, R) はベクトル空間です。Rが体でないときでも、Map(X, R) は有限階数の自由加群なので、有限次元ベクトル空間と大差ないです。

集合S（有限でも無限でもよい）に、有限群Gが右作用している〈act from the right〉とは、次のような写像 act:S×G → G があることです。

act(s, στ) = act(act(s, σ), τ)
act(s, e) = s

actを中置演算子記号・で書けば：

s・στ = (s・σ)・τ
s・e = s

この条件を満たす (S, G, ・) を右G-作用〈right G-action〉または右G-集合〈right G-set〉と呼びます。左G-作用〈左G-集合〉もありますが、今回は右、右だけを使います。

(S, G, ・) と (T, G, ・) が2つのG集合として、f:S → T が次を満たすとき、写像fはG-同変〈G-equivariant〉だといいます。

∀s∈S, σ∈G. f(s・σ) = f(s)・σ

次の条件を満たす f:S → T はG-不変〈G-invariant〉だといいます。

∀s∈S, σ∈G. f(s・σ) = f(s)

これは、t・σ = t と定義したT上のG作用に関してG-同変であることです。つまり、不変性も同変性の一種です。

軌道平均と同変性

(X, G, ・) はG-集合とします。X上の同値関係～を次のように定義します。

x ～ x' :⇔ ∃σ∈G. x' = x・σ

～が実際に同値関係になることは、Gが群であることから従います。この同値関係の同値類をG-軌道〈G-orbit〉または単に軌道〈orbit〉と呼びます。x∈X を含む軌道を [x]_G、混乱の恐れがなければ単に [x] と書きます。

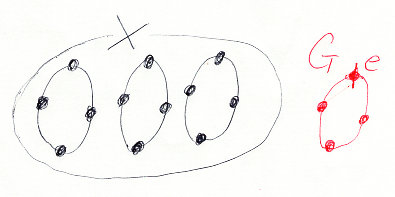
x∈X を固定して、G∋σ $\mapsto$ x・σ∈X を考えると、これが単射になるとは限りませんが、ここでは単射になると仮定します。つまり、X上のG-軌道は、Gと同型な部分集合になります。各軌道の基数（要素の個数）はGの位数（要素の個数）と同じです。「Xの基数＝軌道の本数 × Gの位数」が成立します。

次の図は、Gが4元の群（例えば Z/4Z）で、Xは3つの軌道（各軌道は4元）の直和集合になっている例です。群Gには特別な点である単位元が明確に決まってますが、軌道上に特別な基点はありません*1。

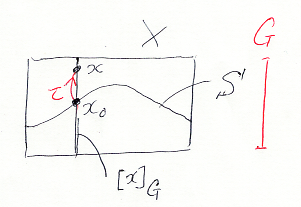
関数 a∈Map(X, R) を各軌道上で平均した関数を考えます。平均を作る作用素を M:Map(X, R) → Map(X, R) とします。Mの定義は：

$\mbox{For }a\in Map(X, R)\\ X\ni x \mapsto M(a)(x) := \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} a(x\cdot \sigma)$

|G| は群の位数（要素の個数）です。aを平均した関数 M(a) は軌道上で同じ値を取ります。別な言い方をすると：

M(a) はG-不変な関数である。

さらに別な言い方では：

M(a) は同値関係～と整合するので、M(a) は商集合 X/～上の関数とみなせる。

単純な平均ではなくて重み付き平均を考えましょう。群Gの要素に重み w:G → R が決まっているとして、重み付き平均 M_w を次のように定義します。

$\mbox{For }a\in Map(X, R)\\ X\ni x \mapsto M_w(a)(x) := \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} a(x\cdot \sigma)w(\sigma)$

ここで、w は群の準同型写像になっているとします。つまり、

w(στ) = w(σ)w(τ)
w(e) = 1

wが群の準同型写像なら、w^-1(σ) := w(σ)^-1 で定義される w^-1 も群の準同型写像です。w^-1 は写像としてのWの逆写像のことではなくて
、Rの乗法逆元を取ることを意味するので注意してください。Rの乗法群は可換群なので：

w^-1(στ) = w^-1(σ)w^-1(τ)
w^-1(e) = 1

平均の重みとなる群準同型写像 w:G → R があるとき、RへのG-作用は次のように定義します。

For r∈R, σ∈G
r・σ := r(w^-1(σ)) （w(σ)の逆元による掛け算）

この前提で、a∈Map(X, R) の重み付き平均 M_w(a) はG-同変になります。それは以下の計算から分かります。

$\:\:\:\: M_w(a)(x\cdot \tau) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} a( (x\cdot\tau) \cdot \sigma)w(\sigma) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} a( x\cdot(\tau \sigma) )w(\sigma) \\$

ここで $\rho = \tau\sigma$ と置くと $\sigma = \tau^{-1}\rho$ 、σを動かして軌道上の総和を取ってもρを動かして軌道上の総和を取っても同じなので、

$= \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} a( x\cdot(\tau \sigma) )w(\sigma) \\ = \frac{1}{|G|}{\displaystyle \sum_{\rho\in G}} a( x\cdot \rho )w(\tau^{-1}\rho) \\ = \frac{1}{|G|}{\displaystyle \sum_{\rho\in G}} a( x\cdot \rho )w(\rho)w^{-1}(\tau) \\ = \left(\frac{1}{|G|}{\displaystyle \sum_{\rho\in G}} a( x\cdot \rho )w(\rho) \right) w^{-1}(\tau) \\ = M_w(a)\cdot \tau$

結局、

$M_w(a)(x\cdot \tau) = M_w(a)\cdot \tau \:\mbox{ on }R$

この同変性は、XへのG-作用だけでなく重み w にも依存するので、丁寧にいうときは (G, w)-同変〈(G, w)-equivariant〉としましょう。

重みとなる群準同型写像 w として、Gの要素をすべて 1 に移す自明な準同型写像 triv:G → R を選ぶと M_triv = M となり、trivによるG-作用に関する同変性、つまり (G, triv)-同変性は不変性となり、重み無し平均のG-不変性が出ます。

以上に説明した、重みの群準同型写像 w に対する線形作用素 M_w:Map(X, R) → Map(X, R) をw-平均化作用素〈w-averaging operator〉と呼ぶことにします*2。

射影としての平均化作用素

a∈Map(X, R) に対して、b = M_w(a) と置くと、前節の結果から b は(G,w)-同変になります。この b に、もう一度w-平均化作用素 M_w を適用してみます。

$\:\:\:\: M_w(b)(x) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} b( x\cdot \sigma) w(\sigma) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} (b( x )\cdot \sigma) w(\sigma) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} b( x ) w^{-1}(\sigma) w(\sigma) \\ = \frac{1}{|G|}{\displaystyle \sum_{\sigma\in G}} b( x ) \\ = \frac{1}{|G|}\times |G| \times b( x ) \\ = b(x)$

計算の途中で、b が(G,w)-同変であることを使っています。下から二行目の ' $\times$ ' は可換環Rでの掛け算です。

この計算で、平均化作用素 M_w:Map(X, R) → Map(X, R) はベキ等性を持つことが分かりました。

M_w $\circ$ M_w = M_w

一般に、R-加群V上の作用素（自己線形写像）P:V → V がベキ等のとき、Pを射影作用素〈projection operator〉、または単に射影〈projection〉と呼びます。w-平均化作用素 M_w は、関数空間 Map(X, R) 上の射影です。

射影 P:V → V に対して、Q := I - P （I = id_V）と置くと、Qも射影になり次が成立します（容易に示せます）。

P² = P, Q² = Q
p $\circ$ Q = Q $\circ$ P = 0 （ $\circ$ は反図式順結合〈合成〉記号、0 はゼロ作用素）
P + Q = I
Im(P) = Ker(Q)
Ker(P) = Im(Q)
V = Im(P) $\oplus$ Ker(P) = Im(P) $\oplus$ Im(Q)
V = Im(Q) $\oplus$ Ker(Q) = Im(Q) $\oplus$ Im(P)

Fix(P) := {v∈V | P(v) = v} と置くと、Pが射影ならば Im(P) = Fix(P) となり、V = Fix(P) $\oplus$ Ker(P) という直和分解が得られます。Fix(P) はいわば“固有値1の固有空間”、Ker(P) は“固有値0の固有空間”です。Fix(P) をPの不動点空間〈fixpoint space〉とも呼びます。射影では、不動点空間と像空間が一致します。

w-平均化作用素 M_w の場合、相方となる射影 I - M_w をD_wと書きw-偏差作用素〈deviation operator〉と呼ぶことにします。M_wとD_w は互いに相補的な射影作用素のペアなので、すぐ上の一般論を適用することができます。

例えば、b∈Im(M_w) であることを次のように言えます。

bは、M_wの像空間に属する ⇔ bは、なんらかの関数 a のw-平均になっている。
bは、M_wの不動点空間に属する ⇔ bのw-平均は再びbになる。
bは、D_wの核空間に属する ⇔ bのw-偏差はゼロになる。

b∈Im(D_w) であることは：

bは、D_wの像空間に属する ⇔ bは、なんらかの関数 a のw-偏差になっている。
bは、D_wの不動点空間に属する ⇔ bのw-偏差は再びbになる。
bは、D_wの核空間に属する ⇔ bのw-平均はゼロになる。

また、(G, w)-同変性との関係では次が言えます。

bは、M_wの像空間に属する ⇔ bは、(G, w)-同変である

'⇒'の方向は、前節で直接計算で示しました。bが(G, w)-同変のとき、M_w(b) = b だったので、bは不動点空間 Fix(M_w) に属します。Fix(M_w) = Im(M_w) なので逆方向も言えます。

同じことですが、言い方を換えると：

bは、D_wの核空間に属する ⇔ bは、(G, w)-同変である

p次対称群と符号のとき

有限群Gが、G = S(p) である特別なケースを考えます。S(p) はp次の対称群で、集合 {1, 2, ..., p} の自己同型写像の集合に写像の結合により群演算を入れたものです。S(p)の位数（要素の個数）は p! なので例えばS(4)は 4! = 24 個の要素を持ちます。S(4)-集合Xが3本のS(4)-軌道を持てば、Xは72個の要素からなる有限集合です。

σ∈S(p) に対して、sign(σ) はσの符号〈偶奇性〉を表します。sign(σ)の値は 1 または -1 ですが、可換環Rの 1, -1 とみなすこととにより、符号 sign:S(p) → R は群準同型写像になります。したがって、S(p)-集合X上で軌道平均を求めるときの重みとして使えます。重み sign による平均化作用素は次のように定義されます。

$\mbox{For }a\in Map(X, R), x\in X\\ M_{sign}(a)(x) := \frac{1}{p!}{\displaystyle \sum_{\sigma\in S(p)}}a(x\cdot \sigma)sign(\sigma)$

M_sign も平均化作用素なので、前節までの一般論が使えます。が、S(p) と sign の場合は独自の言い方をします。sign-平均化作用素 M_sign を交代化作用素〈alternating operator〉と呼びます。関数 a∈Map(X, R) が歪対称〈skew-symmetric〉だとは、次のどれか（すべて同値）と同じことです。

aは交代化作用素M_signの像空間に属する。
aは交代化作用素M_signの不動点空間に属する。
aは(S(p), sign)-同変である。

これで、冒頭に述べた「交代化」と「歪対称」の意味がハッキリしました。

切断上の関数の拡張

G-集合Xの部分集合 S⊆X が次の性質を持つとき切断集合〈section set〉と呼びます。

Sと各軌道の共通部分は常に一点。

x∈X に対して X∩[x] = {x₀} とします。x $\mapsto$ x₀ は一意に決まるので、X → S という写像が定まります。x₀ に適当なGの元 τ を作用させて x を得るので、

x = x₀・τ

このときのτも一意なので、X∋x $\mapsto$ (x₀, τ) ∈S×G という分解も一意的です。

次の図は象徴的（リアリティに欠ける）ですが、今述べた状況を描いています。

切断集合S上でだけ定義された関数 c:S → R があるとき、cをX全体に拡張することを考えます。色々な拡張がありますが、(G, w)-同変になるように拡張します。次のように定義すればいいでしょう。

$\tilde{c}(x) := c(x_0)w^{-1}(\tau)$

ここで、 $\tilde{c}$ は拡張した関数で、x₀, τ は上で説明したxの分解です。この拡張は重みwに依存するので、 $\tilde{c} = E_w(c)$ と書くことにします。この拡張が実際に (G, w)-同変な関数になっているこを確認しましょう。

$\:\:\:\: E_w(c)(x\cdot \sigma)\\ = E_w(c)( (x_0 \cdot \tau) \cdot \sigma)\\ = E_w(c)( x_0 \cdot (\tau \sigma) )\\ = c( x_0 ) w^{-1}(\tau \sigma) \\ = c( x_0 ) w^{-1}(\tau)w^{-1}(\sigma) \\ = E_w(x ) w^{-1}(\sigma) \\ = E_w(x )\cdot \sigma$