部分歪対称関数の歪対称化 - 檜山正幸のキマイラ飼育記 (はてなBlog)

微分形式の計算で、とある式変形がサッパリ分からなかったのですが、組み合わせ的議論がガサッと省略されていました。その組み合わせ的議論をこの記事で補います。背後の事情がなるべく分かるように構成します。「関数の平均・偏差-分解と交代化・歪対称性」は、この記事のための準備として書いた記事なので、必要に応じて参照します。

必要としていた組み合わせ的公式は次のものです。見慣れない言葉や記号がありますが、それらはこの記事内で説明します。

関数 $f: X^{![0, p]} \to R$ が、 $[1, p]$ に関して部分歪対称ならば、次の等式が成立する。

$\mbox{For }\pmb{x} \in X^{![0, p]} \\ {\displaystyle \sum_{ \rho \in S([0, p]) } f(\pmb{x}\cdot \rho) = p!\left( f(\pmb{x}) - \sum_{j = 1}^p f(x_j \,\#\, \pmb{x}'[j\Leftarrow x_0 ] ) \right) }$

[追記]「部分歪対称関数の歪対称化、少し短く」で、ゴチャゴチャした部分を整理した短い記述を述べています。[/追記]

内容：

問題の記述
インデックスに関する前置き
言葉と記号の約束
置換とタプル操作
対称群の埋め込みと置換の分解
上書き代入の公式
簡略な記法と作用の分解
置換の符号
歪対称化作用素の計算

問題の記述

Rは、有理数体Qを含む可換環 *1、Xを集合として、f:X^p+1 → R という関数を考えます。この関数の値を、f(x₀, x₁, ..., x_p) という形に書いたとき、x₁ から x_p に関しては歪対称だとします。

歪対称性に関しては「関数の平均・偏差-分解と交代化・歪対称性」で説明していて、同値な2つの定義があります。

置換（対称群の要素）の作用に関してsign同変である。
歪対称化作用素〈交代化作用素〉の不動点である。

「関数の平均・偏差-分解と交代化・歪対称性」では、「歪対称性」「交代化作用素」という言葉を使ってましたが、不揃いなので「歪対称性」「歪対称化作用素」にします。「歪対称」「反対称」「交代」は同義なので、何を使おうが好みの問題です。

さて、x₁ から x_p に関して歪対称な(p + 1)変数関数をfを、すべての変数 x₀, x₁, ..., x_p （(p + 1)個）に関して歪対称化することを考えます。fは、p個の変数に関しては歪対称なので、その歪対称化は、勝手な(p + 1)変数関数に比べて何かしら簡単な形で表示できるでしょう。歪対称化作用素を SS としたとき、SS(f) の“簡単で扱いやすい表示”を求めることが問題です。

(p + 1)変数関数を、長さ(p + 1)のタプルを引数とする一変数関数と考えます。また、長さ(p + 1)のタプルは {0, 1, ..., p} からXへの写像と考えます。x:{0, 1, ..., p} → X を x = (x(0), x(1), ..., x(p)) あるいはより見慣れた x = (x₀, x₁, ..., x_p) と書くわけです。置換（全単射写像）ρ:{0, 1, ..., p} → {0, 1, ..., p} のタプル x への作用は次の定義で与えられます。

$\pmb{x}\cdot \rho = (x_0, x_1, \cdots, x_p)\cdot \rho := (x_{\rho(0)}, x_{\rho(1)}, \cdots, x_{\rho(p)})$

記号'・'で表される右作用は、写像の結合〈合成〉と同じです。

$\pmb{x}\cdot \rho = \pmb{x}\circ \rho$

Map(Map({0, 1, ..., p}, X), R) 上で定義される歪対称化作用素 SS は次の形です。

$\mbox{For } f:Map(\{0, 1, ..., p\}, X) \to R \\ \mbox{For } \pmb{x} \in Map(\{0, 1, ..., p\}, X) \\ SS(f)(\pmb{x}) := {\displaystyle \frac{1}{(p + 1)!}\sum_{ \rho \in S(\{0, 1, ..., p\}) } f(\pmb{x}\cdot \rho) sign(\rho) }$

ここで、S({0, 1, ..., p}) は(P + 1)次の対称群ですが、0が含まれていることに注意してください。S({0, 1, ..., p}) = BijectiveMap({0, 1, ..., p}, {0, 1, ..., p}) （全単射写像の集合）です。

歪対称化作用素 SS の定義のなかで、定数 1/(p + 1)! は後から調整すればいいので、次の総和について考えます。

${\displaystyle \sum_{ \rho \in S(\{0, 1, ..., p\}) } f(\pmb{x}\cdot \rho) sign(\rho) }$

タプル x の成分として同じ値が出現するときは f(x) = 0 となりますが、最初から、同じ値が出現しないタプルだけを考えることにします（後述）。

インデックスに関する前置き

配列〈リスト | タプル〉のインデックス（成分の番号）を0から始める方式と1から始める方式があります。これは些細な違いですが、両方の方式が混じると、「足す1」や「引く1」をあちこちに挿入する必要があって鬱陶しくなります。今回、定義や計算の途中でこの問題で難儀しました。

「足す1」や「引く1」を挿入するのは、インデックス方式を変換したり揃えようとするからです。相互変換はしないで、そのまま別物として扱うほうがスッキリするようです。そのことに気付いてから定義・計算が捗るようになりました。0始まりインデックスと1始まりインデックスを（統一はしないで）併用するので、その分の準備が複雑になりますが、全体としては単純化された気がします。しかしそれでも鬱陶しいのは事実なので、「スッキリ」は印象と好みの問題かも知れません。

いずれにしても、0始まりインデックスと1始まりインデックスの違いには細心の注意を払う必要があります。なので、0始まりインデックスと1始まりインデックスの区別はくどいほどにしています。あしからず。

言葉と記号の約束

A, B を集合として、写像の集合 Map(A, B) を指数表記で B^A とも書きます。単射の集合と全単射〈双射〉の集合を次の形でも書きます。

B^!A := InjectiveMap(A, B) （ここだけの記法）
S(A) := BijectiveMap(A, A)

A = {1, ..., n} ではなくても、Aがn元の有限集合なら、S(A) をn次対称群と呼びます。このときの群の演算は写像の結合〈合成〉、単位元は恒等写像です。

n, m ∈N に対して、

[n, m] := {k∈N | n≦ k ≦ m}

とします。これは区間の記号ですが、実数の区間は出てこないので混乱はないでしょう。S([1, p]) はp次対称群、S([0, p]) は(p + 1)次対称群になります。

ここでは、「タプル」「リスト」「配列」を区別しません*2。Xの要素を成分〈要素 | 項目 | エントリー〉とする長さnのタプル〈リスト | 配列〉x とは、x:[1, n] → X または x:[0, n - 1] → X です。前者の場合はインデックスが1始まり、後者の場合はインデックスが0始まりです。

タプル〈リスト | 配列〉への置換（対称群の要素）の作用は、写像の結合〈合成〉です。ただし、インデックスが1始まりと0始まりではちょっとだけ違います。

act1:X^{[1, n]} × S([1, n]) → X^{[1, n]}
act0:X^{[0, n - 1]} × S([0, n - 1]) → X^{[0, n - 1]}

インデックス1始まりタプルへの右作用は act1 、インデックス0始まりタプルへの右作用は act0 と区別しました。同様な区別は後でも行います。しかし、右作用の演算子記号'・'はオーバーロード（多義的使用）します*3。

置換とタプル操作

p∈N に対して、p次対称群 S([1, p]) と、(p + 1)次対称群 S([0, p]) を考えます。X成分のタプル〈リスト | 配列〉は、X値の関数とみなすのでした。なので、タプルxのインデックスの集合は dom(x) で、成分の型（値の集合）は cod(x) です。タプルに対する操作〈オペレーション〉 op:X^{[ℓ, n]} → X^{[k, m]} は、ψ:[k, m] → [ℓ, n] によって op(x) = x $\circ$ ψ と書ける場合があります -- この点に注意しながら、幾つかのタプル操作を導入します。

この節で出てくるタプル操作関数名のフルスペルと一言を示しておきます。

関数名	フルスペル	一言
bdown	bubble down	指定成分をバブルダウン（後述）
bup	bubble up	指定成分をバブルアップ（後述）
del	delete	指定成分を削除
rest	rest	先頭を除いた残り
cons	construct	先頭成分を挿入追加
repl	replace	指定成分を置き換え

バブルソートのときに出てくる置換操作が後で重要になります。次の約束をします。

タプルの先頭位置にある成分を指定位置まで動かす操作をバブルアップ〈bubble up〉と呼ぶ。
タプルの指定位置にある成分を先頭位置まで動かす操作をバブルダウン〈bubble down〉と呼ぶ。

置換としてのバブルアップ β0(j):[0, p] → [0, p] を次のように定義します。j は 0（先頭）の行き先です。

β0(j)(0) := j
if (0 < i ≦ j) then β0(j)(i) := i - 1
if (j < i ≦ p) then β0(j)(i) := i

β0 と'0'が付いているのは [0, p] → [0, p] だからで、β1:[1, p] → [1, p] の定義は開始番号がズレます。

β1(j)(1) := j
if (1 < i ≦ j) then β1(j)(i) := i - 1
if (j < i ≦ p) then β1(j)(i) := i

以下は、バブルアップ置換 β0(2):[0, 3] → [0, 3] と β1(3):[1, 4] → [1, 4] の絵です。

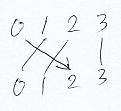
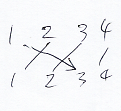
バブルアップ置換をタプルにプレ結合〈pre-compose〉すると、タプル成分のバブルダウン操作になります。アップ・ダウンが逆転するので注意してください。タプルのバブルダウン操作 bdown0(j):X^{[0, p]} → X^{[0, p]} は次のように定義されます。

bdown0(j)(x) := (x_j, x₀, ... x_jが抜けている ...)

これは、

bdown0(j)(x) := x $\circ$ β0(j)

です。同様にして：

bdown1(j)(x) := x $\circ$ β1(j)
bup0(j)(x) := x $\circ$ β1(j)^-1
bup1(j)(x) := x $\circ$ β1(j)^-1

次に、タプル成分の削除操作を定義します。今から定義する削除は、0始まりタプルを1始まりタプルにするものです。del0(j):X^{[0, p]} → X^{[1, p]} は：

del0(j)(x) := (x_j を取り除いて、インデックスは1始まりにする)

del0(j) を正確に定義するには、次の写像 δ(j):[1, p] → [0, p] を考えます。

if (1 ≦ i ≦ j) then δ(j)(i) := i - 1
if (j + 1 ≦ i) then δ(j)(i) := i

そして、del0(j)(x) := x $\circ$ δ(j) と定義できます。

特に、del0(0) を rest0 とします。rest0(x) は、xの先頭成分＝第0成分を取り除いた残り〈rest〉で、インデックスは1から始まります。

rest0((x₀, x₁, ..., x_p)) = (x₁, ..., x_p)

rest0 の“ほぼ逆”の操作として、cons1 を導入します。cons1 は X^{[1, p]} の要素を引数として、X^{[0, p]} の要素を作りだします。cons1:X × X^{[1, p]} → X^{[0, p]}

cons1(a, x) = cons1(a, (x₁, ..., x_p)) := (a, x₁, ..., x_p)

最後に、タプルの成分を他の値で置き換え〈上書き代入 | 破壊的代入〉する関数を定義します。repl1:X^{[1, p]} × [1, p] × X → X^{[1, p]} は：

repl1(x, j, a) := (x_j を a に置き換え、他は同じ)

repl0:X^{[0, p]} × [0, p] × X → X^{[0, p]} も同様に定義できます。

対称群の埋め込みと置換の分解

p次対称群 S([1, p]) を(p + 1)次対称群 S([0, p]) に埋め込みましょう。埋め込み〈embedding〉写像を emb:S([1, p]) → S([0, p]) とします。σ∈S([1, p]) に対する埋め込み emb(σ) ∈S([0, 1]) は次のように定義します。

emb(σ)(0) = 0
emb(σ)(i) = i （1 ≦ i ≦ p）

この埋め込みは、包含関係 S([1, p]) ⊆ S([0, p]) を表現したもので自然な埋め込みでしょう。

自然数 j∈[0, p] とp次置換 σ∈S([1, p]) の組 (j, σ) から、(p + 1)次置換 ρ∈S([0, p]) を作り出せます。そして、(j, σ) ←→ ρ という対応は1：1になります。(j, σ) $\mapsto$ ρ の方向の写像を comb:[0, p] × S([1, p]) → S([0, p]) とすると：

comb(j, σ) := β0(j) $\circ$ emb(σ)

σの自然な埋め込みに、バブルアップ置換をポスト結合〈post-compose〉します。p = 3, j = 2 のケースを絵に描けば次のようになります。

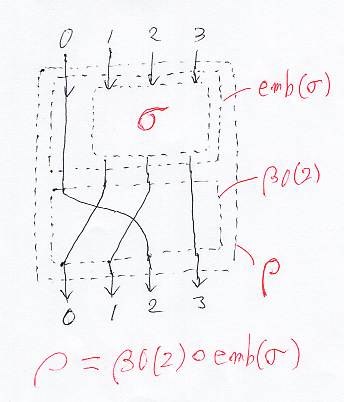
ρから j を得るには j = ρ(0) とします。ρからσを得るには次のようにします。

$\mbox{if } (1 \le i < j) \mbox{ then }\\ \:\:\:\: \sigma(i) := \rho(i) - 1 \\ \mbox{if } (j < i \le p) \mbox{ then }\\ \:\:\:\: \sigma(i) := \rho(i)$

以上で、[0, p] × S([1, p]) $\cong$ S([0, p]) という同型が完全に記述できました。ρ∈S([0, 1]) から j∈[0, p] と σ∈S([1, p]) を得る操作を置換の分解〈decomposition of permutation〉と呼ぶことにします。

上書き代入の公式

後の計算で使う組み合わせ的公式をもうひとつ準備します。タプルに対する上書き代入を、タプル成分の削除とバブルアップで表現します。その公式は次の形です。

$\mbox{For }\pmb{x}\in S([0, p]),\; j\in [1, p] \\ \:\:bup1(j)(del0(j)(\pmb{x}) ) = repl1(rest0(\pmb{x}), j, x_0)$

パッと見では分かりにくいでしょうが、絵で描けば次のようです。図中の☓（Xではない）は、削除でなくなることを意味します。

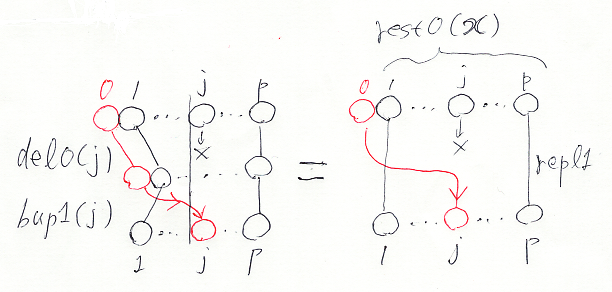
x = (x₀, ..., x_j, ..., x_p) から x_j を取り除きます。ただし、j は 0 ではありません（x₀ は残る）。先頭になった x₀（値は x₀ だが、第1成分）を j 番目の位置までバブルアップします。するとこれは、最初の x_j を x₀ で上書きしたものと同じです。

タプルのバブルアップは、バブルダウン置換 β1(j)^-1 をプレ結合することなので、上書き代入の公式は次の形にも書けます。

$\mbox{For }\pmb{x}\in S([0, p]),\; j\in [1, p] \\ \:\: del0(j)(\pmb{x})\circ \beta1(j)^{-1} = repl1(rest0(\pmb{x}), j, x_0)$

簡略な記法と作用の分解

計算過程を簡略に記述するために、短い記法を導入します。'=:' は、右側が略記であることを示します。

$del0(\pmb{x}, j) =: \pmb{x}\setminus j \:\in X^{[1, p]} \\ rest0(\pmb{x}, j) =: \pmb{x}\setminus 0 := \pmb{x}' \:\in X^{[1, p]}\\ cons1(a, \pmb{y}) =: a \,\#\, \pmb{y} \:\in X^{[0, p]} \\ repl1(\pmb{y}, j, a) =: \pmb{y}[j \Leftarrow a] \:\in X^{[1, p]} \\ comb(j, \sigma) =: j\triangle \sigma \:\in S([0, p])$

この記法を使うと、上書き代入の公式は次のように書けます。

$\mbox{For }\pmb{x}\in S([0, p]),\; j\in [1, p] \\ \:\: (\pmb{x} \setminus j)\cdot \beta1(j)^{-1} = \pmb{x}'[j \Leftarrow x_0]$

' $\circ$ ' が ' $\cdot$ ' に変わっているのは、置換のプレ結合をタプルに対する置換の右作用ともみなせるからです。

後で使う形は両辺にバブルアップ置換を施したものです。

$\mbox{For }\pmb{x}\in S([0, p]),\; j\in [1, p] \\ \:\: (\pmb{x} \setminus j) = \pmb{x}'[j \Leftarrow x_0]\cdot \beta1(j)$

置換 $\rho = j\triangle \sigma \:\in S([0, p])$ のタプルへの作用は次のように書けます（作用の分解）。

$\mbox{For }\pmb{x}\in S([0, p]) \\ \:\: \pmb{x} \cdot \rho = \pmb{x}\cdot (j \triangle \sigma) = x_j \,\#\, ( (\pmb{x}\setminus j)\cdot \sigma )$

ここで、 $(\pmb{x}\setminus j)$ は、タプル $\pmb{x}$ の第j成分を第0位置までバブルダウンしたrest部分（先頭以外）です。これは、置換を $\rho = j\triangle \sigma, \: (j, \sigma)\in [0, p]\times S([1, p])$ と分解すると、その作用も第j成分バブルダウンとrest部分へのσ作用に分解できることを意味します。

置換の符号

置換の符号は、置換を互換〈transposition〉の積で書いたときの互換の個数を k として (-1)^k で与えられます。自然数の順序に関する転倒数としても符号を定義できます。次の関係は基本的です。

$sign(\sigma \tau) = sign(\sigma\circ \tau) = sign(\sigma)sign(\tau) \\ sign(e) = sign(id) = 1 \\ sign(\sigma^{-1}) = sign(\sigma)$

埋め込み emb:S([1, p]) → S([0, p]) で符号が変わらないことは明らかでしょう。

$sign(emb(\sigma)) = sign(\sigma)$

バブルアップ置換、バブルダウン置換の符号は次のようになります。

$sign(\beta0(j)) = sign(\beta0(j)^{-1}) = (-1)^j \\ sign(\beta1(j)) = sign(\beta1(j)^{-1}) = (-1)^{j - 1}$

$j \triangle\sigma$ の符号は次のように求められます。

$\:\:\:\: sign(j \triangle\sigma) \\ = sign(\beta0(j) \circ emb(\sigma)) \\ = sign(\beta0(j)) sign( emb(\sigma)) \\ = (-1)^{j} sign(\sigma)$

歪対称化作用素の計算

準備が整ったので、部分的に歪対称な関数に対する歪対称化作用素（定数倍は無視）を計算しましょう。考える関数は、X^{[0, p]} 全体ではなくて、成分の値が重複するタプルを取り除いた X^{![0, p]} 上で考えます。こうすると、cons1（略記は $\#$ ）、repl1（略記は $[\,\Leftarrow\,]$ ）などの関数は制限を受けます（一部未定義となる）が、この制限が問題になることはありません。

次の総和を計算します。

${\displaystyle \sum_{\rho \in S([0, 1])}f(\pmb{x}\cdot \rho) sign(\rho) }$

置換の分解 ρ ←→ (j, σ) により、次のように書き換えられます。

${\displaystyle \sum_{\rho \in S([0, 1])}f(\pmb{x}\cdot \rho) sign(\rho) } \\ = {\displaystyle \sum_{ (j, \sigma) \in [0, 1]\times S([1, p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) } \\ = {\displaystyle \sum_{j = 0}^p \sum_{ \sigma\in S([1, p]) } f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }$

総和される関数〈summand〉を、作用の分解と上書き代入の公式で変形します。j = 0 のときと、j ≠ 0 のときで場合分けします。

j = 0 のとき：

$\:\:\:\: f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) \\ = f(\pmb{x}\cdot (0\triangle\sigma) ) sign(0 \triangle\sigma) \\ = f(x_0 \,\#\, ( (\pmb{x}\setminus 0) \cdot \sigma ) ) sign(0 \triangle\sigma) \\ = f(x_0 \,\#\, (\pmb{x}'\cdot \sigma) ) sign(\sigma)$

j ≠ 0 のとき：

$\:\:\:\: f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) \\ = f( x_j \,\#\, ( (\pmb{x}\setminus j)\cdot \sigma) ) sign(j \triangle\sigma) \\ = f( x_j \,\#\, ( (\pmb{x}'[j \Leftarrow x_0]\cdot \beta1(j))\cdot \sigma) ) sign(j \triangle\sigma)$

fは、引数タプルのrest部分に対しては歪対称なので、rest部分への置換作用はsignを介して出し入れできます。

$= f( x_j \,\#\, ( (\pmb{x}'[j \Leftarrow x_0]\cdot \beta1(j))\cdot \sigma) ) sign(j \triangle\sigma) \\ = f( x_j \,\#\, \pmb{x}'[j \Leftarrow x_0]) sign(\beta1(j)) sign(\sigma) sign(j \triangle\sigma) \\ = f( x_j \,\#\, (\pmb{x}'[j \Leftarrow x_0] \cdot \sigma) ) sign(\beta1(j)) sign(j \triangle\sigma)$

符号に関しては次が成立します。

$sign(\beta1(j)) = (-1)^{j - 1} \\ sign(j \triangle\sigma) = (-1)^j sign(\sigma)$

結局、j ≠ 0 における総和される関数は、

$\:\:\:\: f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) \\ = f( x_j \,\#\, (\pmb{x}'[j \Leftarrow x_0] \cdot \sigma) ) (-1)^{2j - 1} sign(\sigma) \\ = (-1) f( x_j \,\#\, (\pmb{x}'[j \Leftarrow x_0] \cdot \sigma) ) sign(\sigma)$

総和される関数を、（j は固定したまま）σに関して総和しましょう。fが部分歪対称であること（仮定）を使います。まずは j = 0 のとき：

$\:\:\:\: {\displaystyle \sum_{\sigma\in S([1, p])} f(\pmb{x}\cdot (0\triangle \sigma))sign(0\triangle \sigma) } \\ = {\displaystyle \sum_{\sigma\in S([1, p])} f(x_0 \,\#\, (\pmb{x}'\cdot \sigma)) sign(\sigma) } \\ = p! f(x_0 \,\#\, \pmb{x}') \\ = p! f( \pmb{x})$

次は j ≠ 0 のとき、σに関して総和：

$\:\:\:\: {\displaystyle \sum_{\sigma\in S([1, p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }\\ = (-1) {\displaystyle \sum_{\sigma\in S([1, p])} f( x_j \,\#\, (\pmb{x}'[j \Leftarrow x_0] \cdot \sigma) ) sign(\sigma) }$

fは、引数タプルのrest部分に対しては歪対称、つまり、rest部分への歪対称化作用素に対する不動点なので次が成立します。

さて、σに関して総和したものを j = 0, 1, ..., p に関して総和すると：

$\:\:\:\: {\displaystyle \sum_{j = 0}^p \sum_{\sigma\in S([1, p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }\\ = {\displaystyle \sum_{\sigma\in S([1, p])} f(\pmb{x}\cdot (0\triangle\sigma) ) sign(0 \triangle\sigma) + \sum_{j = 1}^p \sum_{\sigma\in S([1, p])} f(\pmb{x}\cdot (j\triangle\sigma) ) sign(j \triangle\sigma) }\\ = {\displaystyle p! f(\pmb{x}) + (-1)p! \sum_{j = 1}^p f( x_j \,\#\, (\pmb{x}'[j \Leftarrow x_0]) ) }\\ = {\displaystyle p!\left( f(\pmb{x}) - \sum_{j = 1}^p f(x_j \,\#\, \pmb{x}'[j\Leftarrow x_0 ] ) \right) }$