組み合わせ的主バンドル：エディントン・バンドル - 檜山正幸のキマイラ飼育記 (はてなBlog)

エディントン（人名：Eddington）のイプシロンという組み合わせ的関数（を表す記法）があります。その定義や色々な公式は、例えばWikipedia項目に書いてあります。

Wikipedia項目：エディントンのイプシロン

エディントンのイプシロンは、テンソル代数／外積代数の計算で使われますが、その一部分を取り出すと、面白い組み合わせ構造が出現します。微分幾何における主ファイバー・バンドルの組み合わせ（離散有限）版が出てくるのです。エディントンのイプシロン（の一部）は、その主ファイバー・バンドル上の符号関数になります。

内容：

離散ファイバー・バンドル
エディントン・バンドル：最初の定義
エディントン・バンドルへの対称群の作用
G-バンドルと主G-バンドル
主バンドルのセクションと単射の分解
置換の符号とエディントンのイプシロン
タプルによる表現
順列と組み合わせ

エディントンのイプシロンの直接的定義は →「エディントンのイプシロンを圏論的に定義する」

離散ファイバー・バンドル

トポロジー／微分幾何で登場するファイバー・バンドルから、位相的／幾何的な仮定を全部取り除いて、単なる集合と写像だけからなる構造を定義しましょう。そのような構造を離散ファイバー・バンドル（これから定義する）と呼ぶことにします。

(E, B, π)という3つ組を考えます。ここで：

Eは非空な集合で全集合（total set）と呼ぶ。
Bは非空な集合で底集合（base set）と呼ぶ。
πは写像で、全射とする。射影と呼ぶ。

πは全射なので、b∈B に対して、その逆像π^-1(b)は空ではありません。π^-1を、bにおけるファイバー（fibre, fiber）と呼びます。bにおけるファイバーをE_bと書きます。

(E, B, π)のすべてのファイバーが集合として同型なとき、この3つ組が離散的ファイバー・バンドル（discrete fibre/fiber bundle）です。位相的／幾何的な仮定は一切ないことに注意してください。この記事内では離散的ファイバー・バンドルしか扱わないので、離散的ファイバー・バンドルを単にファイバー・バンドルあるいはバンドルと略称します。

バンドル(E, B, π)において、定義より E_b $\stackrel{\sim}{=}$ E_b' （b, b'∈B）ですが、この同型を標準的に与える方法は決まってません。異なるファイバーは同型であっても、自然な対応というものは前もって存在しないのです。

全集合Eは、ファイバー達の直和になるので、次のように書けます。

E = Σ(b∈B | π^-1(b)) = Σ(b∈B | E_b)

エディントン・バンドル：最初の定義

{1, 2, ..., n} = {i∈N | 1≦ i ≦n} という集合が頻繁に出てくるので、これを[n]と書くことにします。[0] = 空集合、[1] = {1} です。p, nを自然数として、Map(p, n)を[p]から[n]への写像の全体とします。Inj(p, n)は[p]から[n]への単射（injection）の全体とします。単射も写像なので、Inj(p, n)⊆Map(p, n) です。

[n]の部分集合で、基数（要素の個数）がpであるもの全体をSubset(p, n)とします。Subset(2, 3)を具体的に書き出してみると：

Subset(2, 3) = {{1, 2}, {1, 3}, {2, 3}}

写像 f:[p]→[n] に対して、その像集合をIm(f)と書きます。Im(f)⊆[n]。写像 f:[p]→[n] が単射の場合は、Im(f)の基数はpです。したがって、Im(f)∈Subset(p, n)。これより、ImをInj(p, n)とSubset(p, n)に制限して、Im:Inj(p, n)→Subset(p, n) と考えても大丈夫です。

基数pの部分集合a（a⊆[n]）を勝手に選ぶと、その集合aを像とするような単射 f:[p]→[n] が存在するので、Im:Inj(p, n)→Subset(p, n) は全射になります。このことから、次のようなファイバー・バンドルが構成できます。

全集合： Inj(p, n)
底集合： Subset(p, n)
射影： Im:Inj(p, n)→Subset(p, n)

n ＜ p だと、Inj(p, n)もSubset(p, n)も空になってしまうので、p ≦ n の範囲だけを考えます。また、ファイバー・バンドルの条件である「すべてのファイバーが同型である」は、現時点では自明でないかも知れません。この条件は後でまた言及しますが、成立しています。

上記のようにして定義された離散ファイバー・バンドルをエディントン・バンドル(Eddington bundle)と呼ぶことにします。命名の理由は、エディントンのイプシロンがこのバンドル（の全集合）上に生息しているからです。

エディントン・バンドルは、p, nの値ごとに定まります。p = 2, n = 3 のときのエディントン・バンドルを絵に描いておきます。絵のなかで、単射 f:[2]→[3] を、(f(1), f(2))というタプルで示しています。

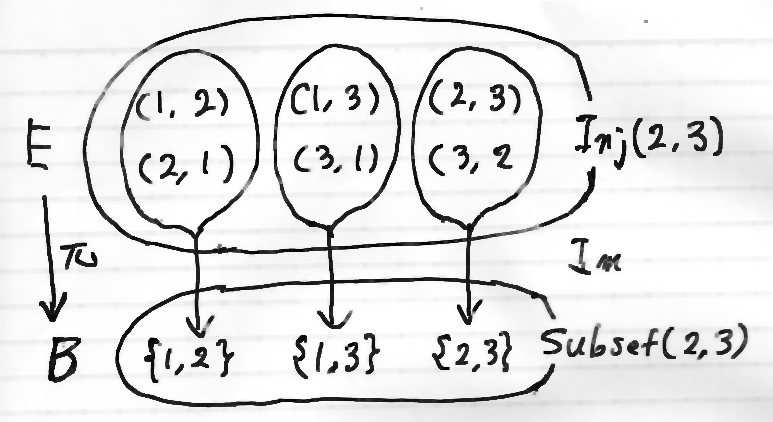
エディントン・バンドルへの対称群の作用

[p]から[n]への双射（1：1の写像）の全体をBij(p, n)と書くことにします。p ≠ n のとき、Bij(p, n)は空になってしまうので、意味があるのはBij(p, p)だけです。f, g∈Bij(p, p) のとき、写像としての結合（composition）f;g（またはg $\circ$ f）が定義できます。恒等写像id_[p]は結合の単位元です。f∈Bij(p, p)ならば逆写像f^-1が存在します。結局、(Bij(p, p), ;, id_[p], (-)^-1)は群になります。

今述べた群構造を備えたBij(p, p)をp次の対称群（symmetric group）と呼びます。対称群の要素である全射は[p]の置換（permutation）と呼ばれます。なので、対称群やその部分群を置換群（permutation group）と呼ぶことがあります。群としてのBij(p, p)、すなわち対称群をS(p)と書きます。Sはsymmetricにちなみます。

群S(p)（集合としてはBij(p, p)）の要素は、σ, τなどのギリシャ文字小文字で表すのが習慣なので、それに従うことにします。σ∈S(p) , f∈Inj(p, n) のとき、σ;f:[p]→[n] は単射になります。よって、写像の結合';'を、S(p)×Inj(p, n)→Inj(p, n) という写像とみなせます。このとき次が成立します。

(σ;τ);f = σ;(τ;f)
id_[p];f = f

写像の結合を反図式順の' $\circ$ 'で書くなら：

f $\circ$ (τ $\circ$ σ) = (f $\circ$ τ) $\circ$ σ
f $\circ$ id_[n] = f

一般に、群 G = (G, ・, e, (-)^-1) と集合Xがあり、さらに (-)▷(-):G×X→X が次の条件（公理）を満たすとき、▷を左G-作用（left G-action）と呼びます。

(α・β)▷x = α▷(β▷x)
e▷x = x

同様に、(-)◁(-):X×G→X が次の条件（公理）を満たすとき、◁を右G-作用（right G-action）と呼びます。

x◁(α・β) = (x◁α)◁β
x◁e = x

群Gは、集合Xに左から（または右から）作用している、とも言います。

対称群S(p)は、集合Inj(p, n)に左から、または右から作用しています。左右の別は趣味の問題です。

S(p)の群演算を図式順結合';'として、集合Inj(p, n)への作用も図式順結合';'とするときは、左作用。
S(p)の群演算を反図式順結合' $\circ$ 'として、集合Inj(p, n)への作用も反図式順結合' $\circ$ 'とするときは、右作用。

左右の別はどっちでもいいのですが、Inj(p, n)へのS(p)作用の重要な特徴として、エディントン・バンドル構造と協調することが挙げられます。S(p)作用は、各ファイバー内で安定しています。つまり、S(p)の要素をいくら作用させてもファイバーから飛び出すことはありません。この状況を正確に記述するために、次節で少し一般論をします。

G-バンドルと主G-バンドル

G = (G, ・, e, (-)^-1)を群とします。(E, B, π)はファイバー・バンドルとします。さらに、バンドルの全集合Eに対して、群Gが右から作用しているとします。右作用を与える写像は ◁:E×G→E です。

このセッティングで、バンドルの構造と右G-作用が協調している（consistent, compatible）とは、次の図式が可換になることです。

  E×G -(◁)→ E
π'｜         ｜π
　 ↓         ↓
   B   ===    B

ここで、π'(x, α) = π(x) です。等式で書くなら：

π(x◁α) = π(x)

π(x) = b と置けば、次のようにも言えます。

x∈E_b ならば、(x◁α)∈E_b

全集合Eの要素xがbのファイバーE_bに入っているなら、Gのどんな要素をxに作用させてもE_bから出ない、ということです。一本のファイバーだけを取り出しても右G-作用を考えることができます。

バンドル(E, B, π)の全集合Eに群Gが右作用（左作用でもOK）していて、その作用がバンドル構造と協調しているとき、Gの作用まで含めてG-バンドル（G-bundle）と呼びます。G-バンドルは、作用◁を添えて、(E, B, π, ◁)と表すことにします。

エディントン・バンドル(Inj(p, n), Subset(p, n), Im)は対称群S(p)の右作用に関してS(p)-バンドルになっています。a∈Subset(p, n)に対するエディントン・バンドルのファイバー(Inj(p, n))_aを、Inj(p, n|a) と書くことにしましょう。

Inj(p, n|a) = {f∈Inj(p, n)| Im(f) = a}

S(p)作用がバンドル構造と協調することは、次のように表せます。

f∈Inj(p, n|a) ならば、(f◁σ)∈Inj(p, n|a) （σ∈S(p)）

これは、単射fの像集合がaのとき、σ;f = f $\circ$ σ の像もaであることなので、確かに成立しています -- 単射に双射を前結合（pre-compose）しても単射のままで、像集合も変化しません。

G-バンドルが主G-バンドル（principal G-bundle）であるとは、各ファイバーがGと（集合として）同型なことです。もう少し正確に言うと、ファイバーE_b内の一点x∈E_bを固定すると、α|→x◁α という写像 G→X が決まります。この写像がGとE_bの双射を与えることです。

エディントン・バンドルの場合、f∈Inj(p, n)を固定したとき、σ|→f $\circ$ σ はS(n)とInj(p, n| Im(f))の同型を与えます。つまり、a∈Subset(p, n)が何であっても、S(p)とInj(p, n|a)は同型です。よって、エディントン・バンドルは主S(p)-バンドルです。

話は前後しますが、a∈Subset(p, n)に対するInj(p, n|a)がすべてS(p)に同型であることから、エディントン・バンドルのファイバーがすべて同型であることが従います。ただし、ファイバーInj(p, n|a)が群構造を持つわけではありません。あくまで“集合として同型”なだけです。

主バンドルのセクションと単射の分解

(E, B, π)がファイバー・バンドルのとき、写像 B→E が s;π = id_B を満たすとき、このバンドルのセクション（section）と呼びます。位相的／幾何的バンドルでは、セクションが存在しないこともありますが（例：メビウス・バンド）、離散的ファイバー・バンドルでは、セクションは必ず存在します。

エディントン・バンドルに対して、標準的セクションを定義しましょう。そのために、[n] = {1, 2, ..., n} の標準的順序構造に注目します。

写像 f:[p]→[n] で、通常の大小順序構造を保存する（order-preserving）写像の全体をOrdMap(p, n) とします。特に、順序を保存する単射をOrdInj(p, n)とします。次の包含関係が成立します。

OrdMap(p, n)⊆Map(p, n)
OrdInj(p, n)⊆OrdMap(p, n)
Inj(p, n)⊆Map(p, n)
OrdInj(p, n)⊆Inj(p, n)

f∈OrdInj(p, n)に対して、fの像集合 Im(f)∈Subset(p, n) が決まりますが、逆に a∈Subset(p, n) に対して Im(f) = a となるfが一意に決まります。fはaの要素を小さい順に列挙する写像です。部分集合aに対して決まる列挙写像をenum(a)と書きましょう。

a∈Subset(p, n) に対して enum(a)∈Inj(p, n|a) ですから、当然に enum(a)∈Inj(p, n) です。Im(enum(a)) = a であることから、enum:Subset(p, n)→Inj(p, n) はエディントン・バンドルのセクションになります。Subset(p, n)の要素（部分集合）を、Inj(p, n)の要素（写像）とみなす標準的方法はこのenumだと言っていいでしょう。

一般に、主G-バンドル(E, B, π, ◁)の場合、セクション s:B→E があると、同型写像 φ:B×G→E を構成できます。φの具体的な表示は：

φ(b, α) = s(b)◁α

s(b)がファイバーE_bの“基点”を与えます。同じファイバー内の他の点は、群Gの要素をs(b)に作用させれば得られます。主バンドルでは、ファイバーとGが同型なのでこのような同型φが構成可能なのです。

エディントン・バンドルの場合は、(a, σ)|→enum(a) $\circ$ σ として Subset(p, n)×S(p)→Inj(p, n) の同型が構成できます。つまり、Inj(p, n)の要素（単射）fは、[p]の置換σを選ぶことにより、f = enum(Im(f)) $\circ$ σ と一意的に表現できます。

これは、単射 f:[p]→[n] は、置換 σ:[p]→[p] と順序保存単射 f':[p]→[n] に一意的に分解（factorization）できるという、分解定理ともみなさます。

置換の符号とエディントンのイプシロン

置換 σ∈S(p) に、偶置換か奇置換かに応じて+1, -1を対応させる写像を（置換の）符号（sign, signature）と呼びます。符号を sgn:S(p)→{+1, -1} とします。（符号について、ここでは詳しく説明しません。）

符号関数を、S(p)からInj(p, n)に拡張します。前節の f = f' $\circ$ σ という一意分解を使います。ここで、f' = enum(Im(f)) です。fからσは一意に決まるので、esgn(f) := sgn(σ) と定義します。esgn（extended sign）は、esgn:Inj(p, n)→{+1, -1} という写像になります。

エディントンのイプシロンは、ε:Map(p, n)→{+1, 0, -1} という関数です。εの定義域は自然数p, nに依存するので、εⁿ_pと書くほうが正確ですが、混乱がないならp, nは省略します。εの定義は次のとおりです。

ε(f) = 0 if (fが単射でない)
ε(f) = esgn(f) if (fが単射)

対称群S(p)は、前結合（pre-composition）によりMap(p, n)全体に作用します。また、群({+1, -1}, (掛け算), +1)は群であり、集合{+1, 0, -1}に掛け算により作用します。対称群S(p)上の符号sgnと、Map(p, n)上のエディントンのイプシロンは、2つの群作用のあいだを繋ぐ準同型を構成します。つまり：

ε(f $\circ$ σ) = ε(f)・sgn(σ) （・は掛け算）

タプルによる表現

Map(p, n)の要素 f:p→n は、{1, 2, ..., n}を成分とする長さpのタプル(f(1), f(2), ..., f(p))で表現できます。Inj(p, n), S(p), OrdMap(p, n), OrdInj(p, n)などの要素も制限付きのタプルとして表現できます。タプル成分に対する制限は次のとおりです。

f∈Map(p, n) ならば、1 ≦ f(1), f(2), ..., f(p) ≦ n
f∈Inj(p, n) ならば、1 ≦ f(1), f(2), ..., f(p) ≦ n で f(1), f(2), ..., f(p) はすべて異なる。
f∈S(p) ならば、1 ≦ f(1), f(2), ..., f(p) ≦ p で f(1), f(2), ..., f(p) はすべて異なる。
f∈OrdMap(p, n) ならば、1 ≦ f(1) ≦ f(2) ≦ ... ≦ f(p) ≦ n
f∈OrdInj(p, n) ならば、1 ≦ f(1) ＜ f(2) ＜ ... ＜ f(p) ≦ n

エディントンのイプシロンの定義や、その他の組み合わせ的議論もタプルをベースに行うことが多いのですが、見通しが良くないので、すべて有限集合のあいだの写像として記述しました。必要があれば、タプルに関する言明に翻訳できます。

順列と組み合わせ

高校で習った順列・組み合わせと、エディントン・バンドルの関係を述べておきましょう。

n個のモノからp個を選んで並べたモノが順列です。この順列とはInj(p, n)の要素のことです。「Inj(p, n)の要素の“タプル表現”が順列」と言ったほうがより正確かも知れません。順列の総数を_nP_pと書きますが、これは集合Inj(p, n)の基数に他なりません。集合Xの基数をcard(X)と書くことにするなら：