最近、次男(未就学児)は、20くらいまでの数の勘定と一桁の足し算ができるようになりました。足し算は指を使ってします。結果が10を超えると指が足りなくてできないので、当てずっぽうで答を言うのはおにいちゃんと同じです(苦笑)。
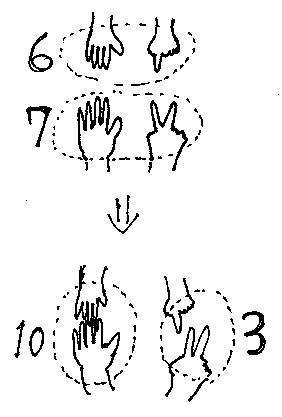
そこで、僕が手を貸して(文字通り、手の指を貸す)6+7 の計算をやってみました。次の絵のような感じです。
普通の計算式で表すなら:
(a)から(b)に移るところを丁寧にやれば、結合律(結合法則;associative law)と可換律(交換法則;commutative law)を何度か使うことになります。このことから、指を使った足し算の基礎は、足し算の結合律と可換律だとも言えるでしょう。
6+7
=(5+1)+(5+2) …(a)
=(5+5)+(1+2) …(b)
=10+3
=13
しかし僕は、どうも違うような印象を抱きました。6を5+1、7を5+2に置き換えたときの「+」って、これホントに足し算でしょうか? まーもちろん、フォーマルには足し算なんですけど、感覚的には「分け算」とでもいうか、「6を、5と1に分けて考える」ってことですよね。あるいは「6は、5と1が合わさったものだと考える」ってこと(合わせ算か?)で、「あっちから6、こっちから7を持ってきて、全部一緒にする」という“本格的操作”である「足し算」とは区別すべきじゃないかと。
そこで、「6は、5と1が合わさったもの」という言明は 6=5#1 という書き方にします。「#」も演算記号ですが、足し算とは心情的に別なものです。次男の実際の行為からいっても、演算#は指の配置パターンの再認識に過ぎませんが、演算+は指を全部一緒にしたグループを再構成して、さらに数え直しが要求されるのです。
演算#と+を使った計算は次のようなものです。指の絵と比べてください。
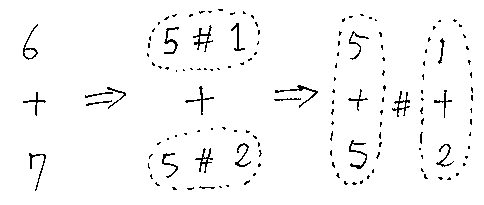
6+7
=(5#1)+(5#2) …(a)
=(5+5)#(1+2) …(b)
=10#3 …(c)
=13
(5+5)に対して次男は数え直しをしてませんが、それは10の特殊性によるもので、原則は数え直しでしょう*1。(1+2)は実際「1、2、3」と数え直しをしてます。(c)の部分が+でなくて#なのは、「10と3が合わさったものが13」(「13は、10と3が合わさったもの」)は、パターン認識だと思われるからです。
となると、(a)から(b)に移るときに使われているのは、結合律と可換律の組み合わせというより、むしろ次の法則だと言うべきでしょう。
- (a#b)+(c#d) = (a+c)#(b+d)
これ、何かと似てませんか? 回路素子(素子を組み合わせた回路も再び素子と考える)の直列/並列の接続を思い出してください。次の図の2つの接続(並列は単に配置するだけ)は、機能/効果においては同等です。
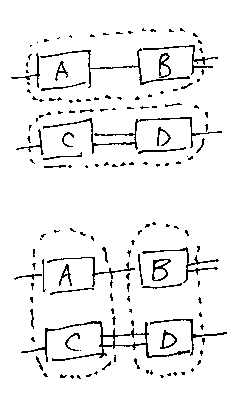
直列接続を#、並列接続を+と書くと:
- (A#B)+(C#D) = (A+C)#(B+D)
2つの演算に関する、この形の等式は、interchange law(僕は交替律<こうたいりつ>という訳語を使ってます)と呼びます。
「ETBダイアグラム」という記事の第4節に、同じような図と等式(C, Dの変わりにA', B'ですが)が出現します。実は、交替律はモノイド圏(monoidal category;モノイダル圏、単圏とも呼ぶ)という構造の基本的法則なのです。
回路素子達は、直列接続と並列接続の2つの演算に関してモノイド圏になります。プログラム(の何らかの数理モデル)の全体も、順次(シーケンシャル)結合と並列(パラレル)結合の2つの演算に関してモノイド圏になります。
子供の足し算の世界も、“パターンの再認識演算#”と“一緒にして数え直す演算+”に関してモノイド圏*2になっているような気がするんですよね。もっとも、これって、僕の圏論バイアスが入ったコジツケ的見方だからあてにならないけど。