図式思考の例として、ラックス・モノイド関手について考えてみる

圏論に自然変換の概念が入ってくると、2-射を持つ2次元の圏（「圏の圏」です）を扱うことになります。圏の直積も普通に使います。例えば、二項関手〈双関手〉の定義には圏の直積が必要です。直積は、関手にも自然変換にも定義できます。その結果、「圏の圏」は「直積を持つ2次元の圏」となります。

直積を持つ2次元の圏のなかでは、横結合、縦結合、直積という三種類の演算があり、計算は2次元／3次元的なものになります。文字・記号を1次元的に並べたテキストでは無理があり、絵図〈picture | diagram〉による記述と計算が必要になります。

ここでは、ラックス・モノイド関手の結合律と単位律を例にして、高次元の圏的構造〈higher dimensional categorical structure〉の絵図表現〈{pictorial | diagrammatic | graphical} {presentation | representation}〉を紹介します。

また、本文と独立に読める付録として、ストリング図とストライプ図の関係を説明します。

内容：

ラックス・モノイド関手
ストリング図書き換え
ラックス・モノイド関手の素材
ラックス・モノイド関手の結合律と単位律
ストリング図とストライプ図

ラックス・モノイド関手

モノイド圏、各種モノイド関手、モノイド自然変換については、以下の記事を参照してください。だいたいの雰囲気を知っていればいいです、完全な理解は要求してません。

次の記事にも関連する内容があります。

モノイド、モナド、ラックス・モノイド関手は似ています。似ているのには理由があるのですが、今はその理由には踏み込みません*1。注意すべきことは、ラックス・モノイド関手が単なる関手（プレーンな関手）ではなくて、モノイドやモナドと類似の代数構造であることです。これは、乗法と単位を持ち、結合律と単位律を満たすことを意味します。

	モノイド	モナド	ラックス・モノイド関手
台	集合	自己関手	関手
積	集合の直積	自己関手の結合	関手とモノイド積の組み合わせ
乗法と単位	写像	自然変換	自然変換

ストリング図書き換え

前節で参照した過去記事では、ラックス・モノイド関手の記述と計算は主にストライプ図〈stripe diagram〉を使っています。今回は別な描画法を紹介します。ブルース・バートレット〈Bruce Bartlett〉によるストリング図書き換え〈string diagram rewriting〉です。次の論文で説明されています。なお、バートレット自身は、ストリング図をワイヤー図〈wire diagram〉と呼んでいます。

Title: Quasistrict symmetric monoidal 2-categories via wire diagrams (7 Sep 2014)
Author: Bruce Bartlett
Pages: 18p
URL: https://arxiv.org/abs/1409.2148

次のような3次元的状況を考えます。右側に“3次元図を見ている人”がいるとします。この人から見ると、二重矢印の α は、自分に向かって来るように見えます。

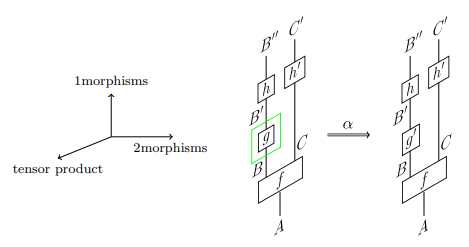
この状況を紙面（あるいは画面、{ホワイト | ブラック}ボード）に描くときは次のようにします。

重要な点は：

奥から手前に向かってくる2-射 α を、紙面の左から右に向かって描く。

この約束により、「左側のストリング図を、αにより、右側のストリング図に書き換えた」とみなします。

縦方向は、1-射の横結合の方向になります。バートレットによる注意を引用すると：

Unfortunately, what is usually called vertical composition $\circ$ of 2morphisms runs horizontally in wire diagrams, and what is usually called horizontal composition ＊ runs vertically!
不幸なことに、2射の縦結合と呼ばれている演算 $\circ$ はワイヤー図では横方向になり、横結合と呼ばれる演算＊は縦方向になる！

この程度の不幸は日常茶飯事です。気にしたり嘆いたりしないでサッサと割り切りましょう。そもそも、縦と横の選択に根拠・必然性がないので、縦結合と名付けられているからといって縦に書くべき筋合いなんてないのです*2。

[補足]以前、「縦のものを横にされてしまうと辛い」と書いたことがあるので、誤解されないように補足しておくと、これは「横のものも縦のものも、なんでも横にされてしまうと辛い」です。つまり、2次元のトポロジー／レイアウトの情報を潰されるとデコードが大変すぎて辛いってことです。縦を横に、横を縦にされるのも嬉しくはないですが、まーしょうがないです。

縦横上下左右の変更には対応せざるを得ないので、対応力をトレーニングしましょう。

双対や随伴に強くなるためのトレーニング

[/補足]

この記事で使うルールは、バートレットとは少し違うのでまとめておきます。

テキスト記法は図式順記法として演算子記号は「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」に従う。
紙面の横方向は直積の方向として、左から右に見る。つまり、Fの右横にGが書いてあったら、F×G と解釈する。
紙面の縦方向は横結合の方向として、上から下に見る。つまり、Fの下にGが書いてあったら、F＊G と解釈する。（縦方向が横結合ですよ！）

もうひとつバートレットの注意を引用しておきます。

it will usually just be drawn flat in the page (but the three-dimensional picture should be kept in mind),
図は、ページにフラットに描かれるが、3次元的な絵を心に持ち続けるべきである。

ラックス・モノイド関手の素材

まず、記号の乱用と省略の話。いつのように、C = (C, $\otimes$ , I) のような記号の乱用をします。C, D が2つのモノイド圏のとき、それぞれのモノイド積／単位対象は別物なので、C = (C, $\otimes$ _C, I_C), D = (D, $\otimes$ _D, I_D) と書くべきでしょうが、どれも $\otimes$ , I と書くことがあります。二項演算子記号 ' $\otimes$ ' を関手記号にするときは、Haskell風の '( $\otimes$ )' （丸括弧で包む）を使うことがありますが、丸括弧を付けることさえ横着して、 $\otimes$ :C×C→C のように書くかも知れません。だいぶモノグサするのでご注意ください。

我々が扱うモノイド圏は小さいものに限定しましょう。モノイド圏達が定義される環境・世界は、小さい圏の2-圏Catです。単に関手といえば、Catの射のことで、単に自然変換といえばCatの2-射のことです。モノイド圏、モノイド関手、モノイド自然変換は、Catの 0, 1, 2-射を組み合わせて作る構造物です。

C, D はモノイド圏として、関手 F:C→D が厳密モノイド関手だとは、次の可換性が成り立つことです。

$\require{AMScd} \newcommand{\hyph}{\mbox{-}}% \newcommand{\cat}[1]{{\mathcal {#1}}}% \newcommand{\incat}{\:\: \mbox{in}\:}% \newcommand{\NE}{\nearrow\!\!\!\nearrow} % \newcommand{\NW}{\nwarrow\!\!\!\nwarrow} % \newcommand{\SE}{\searrow\!\!\!\searrow} % \newcommand{\SW}{\swarrow\!\!\!\swarrow} % \newcommand{\For}{\mbox{For}\:\:} % \newcommand{\Comm}{\mbox{commutative}} % % \begin{CD} \cat{C}\times\cat{C} @>{F\times F}>> \cat{D}\times\cat{D} \\ @V{\otimes_\cat{C}}VV @VV{\otimes_\cat{D}}V \\ \cat{C} @>{F}>> \cat{D} \end{CD}\\ \Comm \incat {\bf Cat}$

「可換図式とペースティング図」で述べたように、図式の可換性を'eq'でマークすると：

$\begin{CD} \cat{C}\times\cat{C} @= {} @>{F\times F}>> \cat{D}\times\cat{D} \\ @V{\otimes_\cat{C}}VV @.{\SW eq} @VV{\otimes_\cat{D}}V \\ \cat{C} @>{F}>> {} @= \cat{D} \end{CD}\\ \incat {\bf Cat}$

'eq' は等号なので、上のペースティング図は (F×F); $\otimes$ = $\otimes$ ;F を意味します。A, B∈|C| を取って成分表示すれば：

F(A) $\otimes$ F(B) = F(A $\otimes$ B) on |D|

'eq' を等号（恒等自然変換）とは限らない自然変換 μ に置き換えると：

$\begin{CD} \cat{C}\times\cat{C} @= {} @>{F\times F}>> \cat{D}\times\cat{D} \\ @V{\otimes_\cat{C}}VV @.{\SW \mu} @VV{\otimes_\cat{D}}V \\ \cat{C} @>{F}>> {} @= \cat{D} \end{CD}\\ \incat {\bf Cat}$

この μ がモノイド関手の乗法です。

F:C→D が単位対象を厳密に保存することは、次の等式で書けます。

F(I) = I on |D|

これは、次の可換図式としても表現できます。

$\begin{CD} ☆ @>{(I_\cat{C})^\sim}>> \cat{C} \\ @| @VV{F}V \\ ☆ @>{(I_\cat{D})^\sim}>> \cat{D} \\ \end{CD}\\ \Comm \incat {\bf Cat}$

ここで：

☆は、単一の対象と恒等射だけを持つ自明圏
対象 A∈|C| に対して、A^~:☆→C は、Aをポイントするポインティング関手

(I_C)^~ = (I_D)^~ は、F(I) = I と同じことです（I_C = I, I_D = I と略記）。

等式（恒等自然変換）を自然変換 η に置き換えると：

$\begin{CD} ☆ @= {} @>{(I_\cat{C})^\sim}>> \cat{C} \\ @| @.{\NE\eta} @VV{F}V \\ ☆ @>{(I_\cat{D})^\sim}>> {} @= \cat{D} \\ \end{CD}\\ \incat {\bf Cat}$

以上に述べた、μ, η がラックス・モノイド関手（一種の代数系）の素材です。

μ :: (F×F)＊ $\otimes$ ⇒ $\otimes$ ＊F : C×C→D in Cat
η :: I^~ ⇒ I^~＊F : ☆→D in Cat

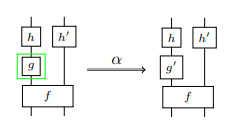
これらをストリング図書き換えで描けば：

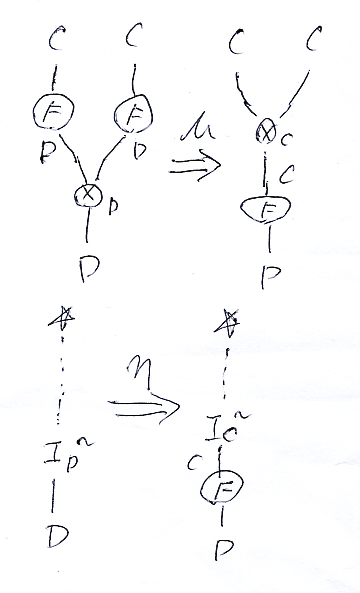
既に注意したように、横方向が直積（記号'×'）、縦方向が横結合（記号'＊'）です。☆を表すワイヤーは点線にします。

簡略化して描いたストライプ図書き換えは次のようになります。

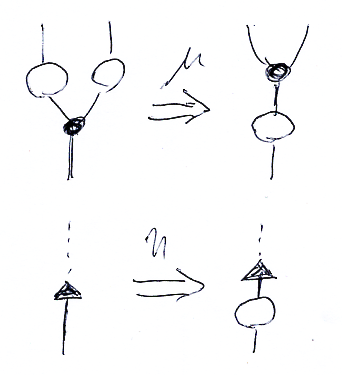
関手 F はラベルなしの白丸で略記。
モノイド積・二項関手 $\otimes$ はラベルなしの黒丸で略記。
単位対象のポインティング関手 I^~ は黒三角で略記。

書き換え（実体は自然変換）μ, η をストライプ図で描けば次のようになります。

ストリング図とストライプ図の関係は後でまた述べますが、ここで注意すべきは；ストリング図の点線は自明圏☆を表しますが、ストライプ図の点線は単位対象のポインティング関手 I^~ を表していることです。ストリング図の黒三角がストライプ図の点線です。

関手 F、自然変換 μ, η はあくまで素材〈ingredient | constituent〉なので、これらがラックス・モノイド関手になるための条件〈法則 | 公理〉が別にあります。

ラックス・モノイド関手の結合律と単位律

ラックス・モノイド関手の結合律と単位律は、次の記事で（ストライプ図を使って）書いています。

ストライプ図の利用例は：

法則の記述法としては、次の記事も参考になるかも知れません。

マックレーンの五角形をインデックスなしの等式で表す

上記記事内で、マックレーンの五角形を次のように描きました。これもストリング図書き換えによる描画です。

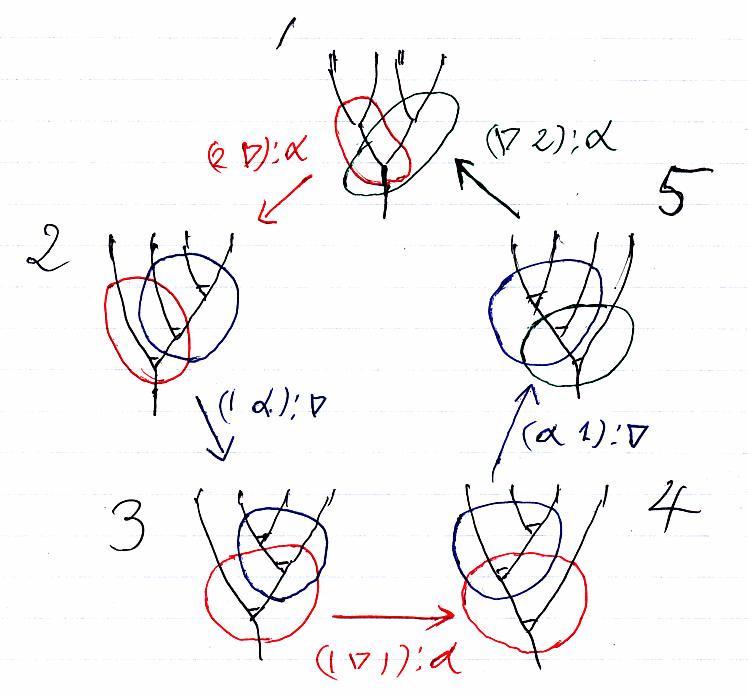
同じ描画法で、ラックス・モノイド関手の結合律と左単位律を描いてみると次のようになります。右単位律は左単位律と同様なので省略。

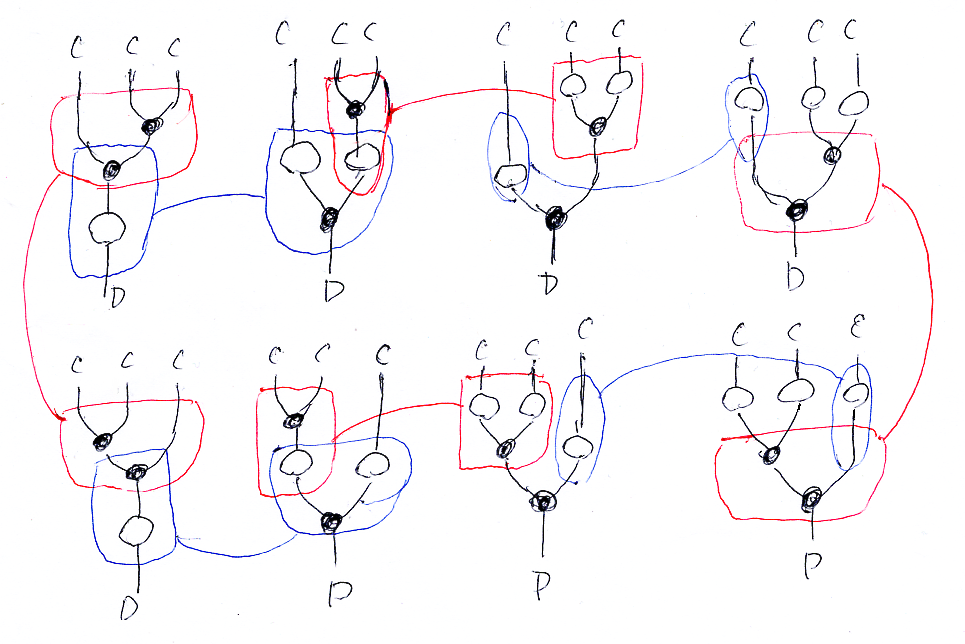
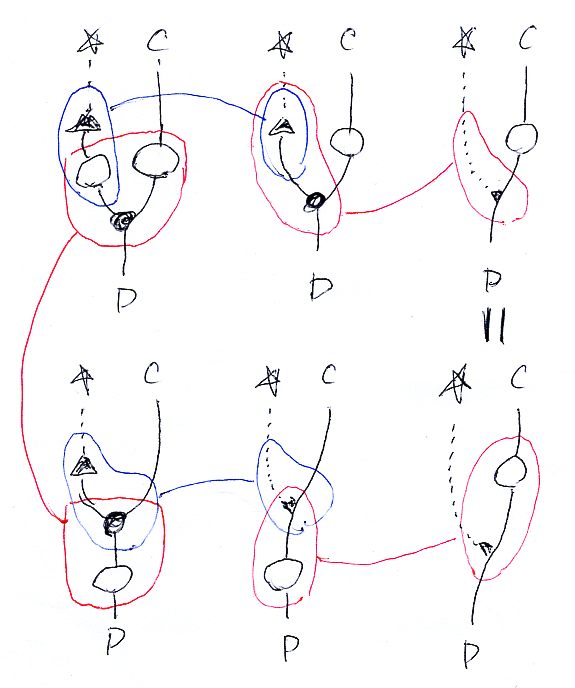
タイト・モノイド関手、反ラックス・モノイド関手のときも使えるように、書き換え（自然変換）の方向は書いてません。一群のストリング図達が書き換えによって相互に繋がれている状況です。

特定のストリング図を指定するために、「結合律・下段2番」のように呼ぶことにします。上段・下段とも、左から右に便号をふることにします。

結合律は8つのストリング図のあいだの書き換えですが、「上段3番←→上段4番」、「下段3番←→下段4番」の書き換え（交替律による）は省略していいかも知れません。逆に、丁寧に書けばストリング図はもっと増えます。「上段1番←→下段1番」、「上段4番←→下段4番」では、(C×C)×C $\cong$ C×(C×C) （直積の結合律同型）を使っているので、これを明示するとストリング図は10個になります。単位律の場合も、記述の丁寧さでストリング図の個数は変わります。

これらのストリング図書き換えがそれぞれ結合律、左単位律という等式を表しています。等式と解釈するためには左辺と右辺が必要です。そのためには、書き換えのスタートとゴールを決めて、スタートからゴールに至る2つの書き換えパスを左辺と右辺にします。

例えば、結合律に関する2つの書き換えパスは：

下段4番 → 上段4番 → 上段3番 → 上段2番 → 上段1番
下段4番 → 下段3番 → 下段2番 → 下段1番 → 上段1番

左単位律に関する2つの書き換えパスは：

上段3番 → 上段2番 → 上段1番 → 下段1番
上段3番 = 下段3番 → 下段2番 → 下段1番

書き換えは自然変換で、書き換えの順次実行は自然変換の縦結合になるので、自然変換に関する等式が得られます。

絵をテキストで表現することは、記述と計算の観点からは意味ありませんが（絵で記述・計算すればよい）、異なる言語（絵図言語とテキスト言語）のあいだの翻訳としては意味があります。「下段4番 → 上段4番」という書き換えだけテキスト化してみましょう。

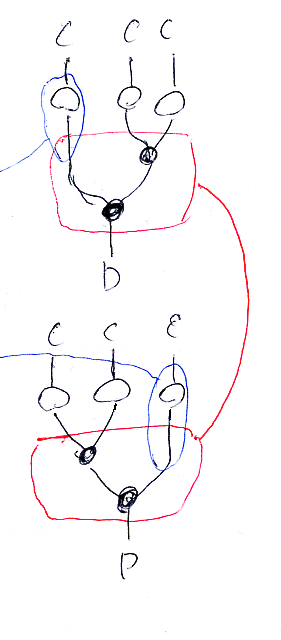
まず、書き換えの方向は下から上だとしてレイアウトをそのまま写し取ると：

$\begin{CD} \begin{matrix} F\times\ F\times F \\ Id_{\cat{D}} \times (\otimes_\cat{D}) \\ (\otimes_\cat{D}) \end{matrix} \\ @AA{\begin{matrix}ID_{F\times\ F\times F} \\ \alpha^\cat{D} \end{matrix}}A \\ \begin{matrix} F\times\ F\times F \\ (\otimes_\cat{D}) \times Id_{\cat{D}} \\ (\otimes_\cat{D}) \end{matrix} \end{CD}$

ここで、

(F×F)×F と F×(F×F) の区別をせずに F×F×F と書いてます。
Id は恒等関手
ID は恒等自然変換
α^D は、モノイド圏Dの結合律子 α^D::( $\otimes$ ×Id)＊ $\otimes$ ⇒(Id× $\otimes$ )＊ $\otimes$

次に、縦方向のスタックは上から下への横結合なので、横結合記号'＊'を挟んで横向きに書いて、矢印の方向は左から右へと変更します。

$\begin{CD} (F\times\ F\times F) * ( (\otimes_\cat{D}) \times Id_{\cat{D}} ) * (\otimes_\cat{D}) @>{ID_{F\times\ F\times F}\, *\, \alpha^\cat{D}}>> (F\times\ F\times F) * (Id_{\cat{D}} \times (\otimes_\cat{D}) ) * (\otimes_\cat{D}) \end{CD}$

反図式順記法なら、横結合記号を変えて左右を入れ替えます。

$\begin{CD} (\otimes_\cat{D}) \cdot ( (\otimes_\cat{D}) \times Id_{\cat{D}} ) \cdot (F\times\ F\times F) @>{\alpha^\cat{D}\, \cdot\,ID_{F\times\ F\times F}}>> (\otimes_\cat{D}) \cdot (Id_{\cat{D}} \times (\otimes_\cat{D}) ) \cdot (F\times\ F\times F) \end{CD}$

書き換えごとに矢印を1本作って、それらを適当な多角形にレイアウトした可換図式を作れます。その可換図式をさらにテキスト化してもいいですが、僕はやる気になれません。

他の表現方法として、等式の左辺・右辺をそれぞれペースティング図にして、ぺースティング図の等式とすることもできます。ペースティング図の等式の例は「可換図式とペースティング図」にあります。

いずれにしても、絵をテキスト化するのは労力がかかります。それで僕が疲労困憊した記録が次の記事にあります。

ストリング図とストライプ図

ここから先は付録です。今までの話とは独立に読めます。関手と自然変換を表すストリング図とストライプ図の関係を見ていきます。ストリング図については、「圏論の随伴をちゃんと抑えよう：お絵描き完全解説」の第3節（「図式順記法と混合記法」）まで読めば十分です。

F:C→D を関手とします。A∈|C| に対して、ポインティング関手〈ポインター関手〉 A^~:☆→C が決まります。ここで、☆は単一の対象と恒等射だけを持つ自明圏〈単位圏 | 終圏〉です。関手の図式順結合（横結合とみる）を'＊'で表すと：

A^~＊F = F(A)

A^~:☆→C を A∈|C| と同一視して単に A と書くことがあります。

今の状況は、次の図の上段のように書けます。上段のストリング図の次元を1次元上げて、圏を部屋（3次元）、関手を壁（2次元）で描くと下段のようになります。

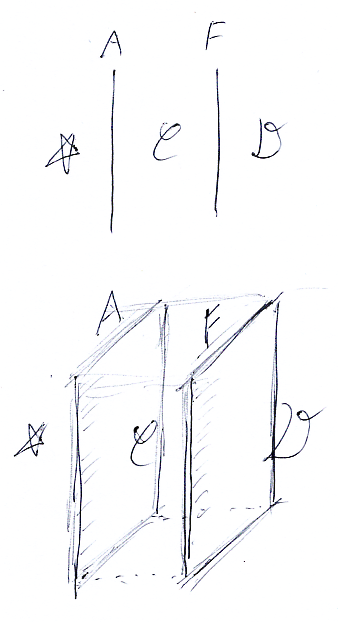
壁Aに一本の線を描いて、壁Fに短冊状の窓を付けます。窓は色付き半透明として、部屋Dにいる人が窓から線を眺めた絵がストライプ図です。

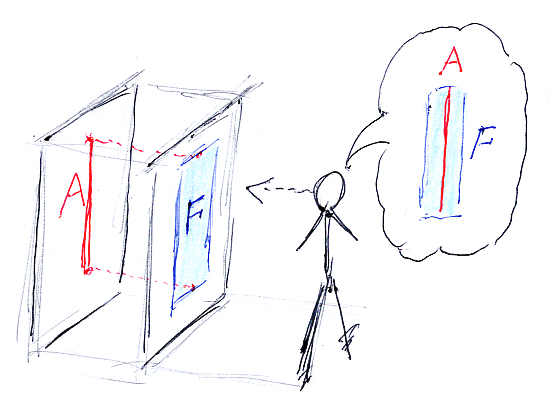
自然変換 α::F⇒G:C→D がある場合も同じように考えて、αの成分表示 α_A:F(A)→G(A) in D のストライプ図が得られます。

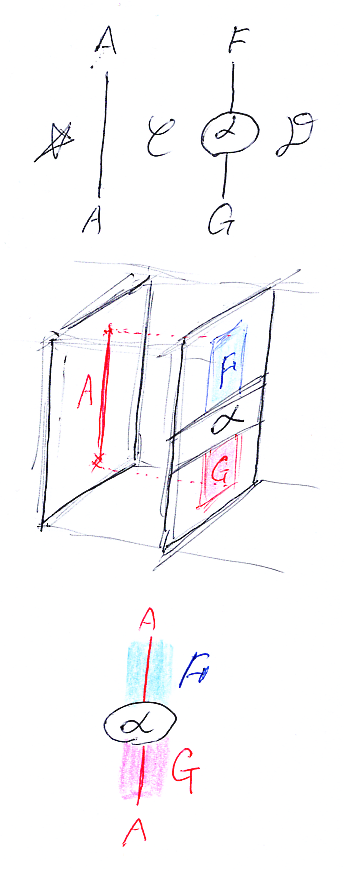
ストリング図における横結合、例えば A＊α＊H は、ストライプ図では入れ子になります。α＊H（これは自然変換と関手の横結合＝α＊ID_H）のA成分を、部屋Eから眺めた図が下段のストライプ図です。

ストライプ図は横結合に奥行き方向（横断方向）を使うので、横方向は余っています。なので、横方向は直積の方向として使うことにします。(F×F’)＊H の (A, B)成分は次のように書きます。

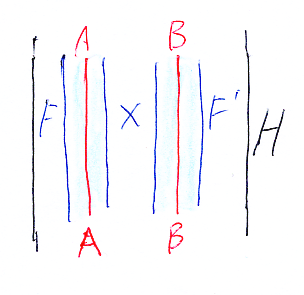
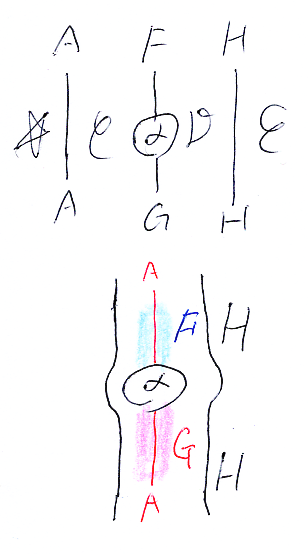
この状況を、再びストライプ図で描いてみます。下の左側のストリング図では、圏がワイヤー（1次元）、関手がノード（0次元）です。縦方向が横結合方向で、横方向は直積方向です。一方、右側のストリング図は、圏が領域（2次元）、関手が線（1次元）、横方向が横結合方向で縦方向が直積方向です。

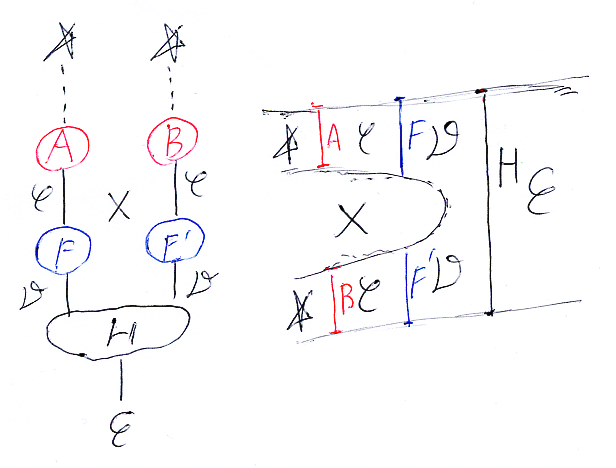
上の右側のストリング図の次元を上げて、圏を部屋（3次元）、関手を壁（2次元）にします。先程と同じように、赤い線を描き短冊状の半透明窓を作ると、部屋Eから見た眺めとしてストライプ図が再現します。このストライプ図の横方向は直積方向になります。

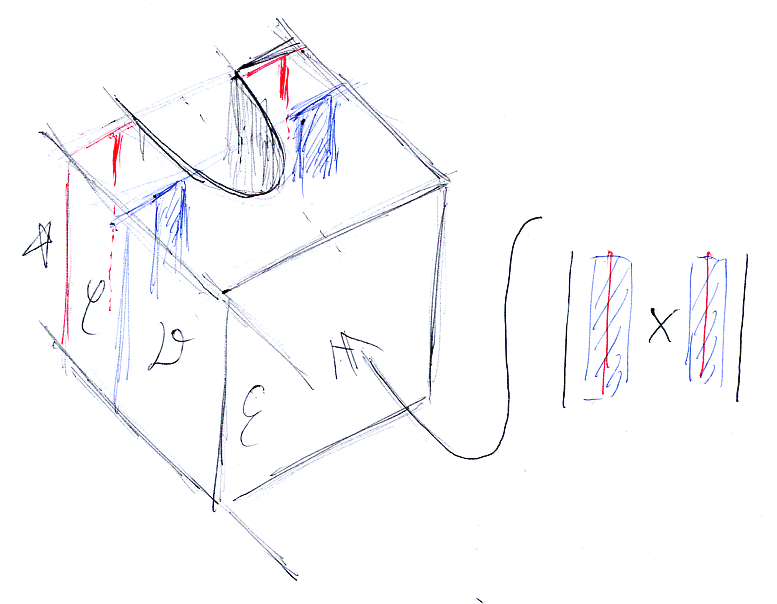
関連する話題が次の記事にあります。

新しい絵算手法：ストリング＋ストライプ図

必要に応じて、縦横上下左右も次元も変更しながら、色々な観点から描画しましょう。

*1:似てる理由を一言でいえば、どれも 3-圏のホム2-圏 BICAT^lax(K, L) で記述できるからです。関連すること（ヒント）は、「モナド、双圏、変換手」にあります。

*2:縦横ではなくて、左右の選択もまったく根拠がないので覚えられない、という話は「ガーッ! また左と右が。カン拡張」