このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

反ラックス・モノイド関手の一般余結合律

雑記／備忘

\mathcal{C}, \mathcal{D} がモノイド圏のとき、反ラックス・モノイド関手 F = (F, \delta, \varepsilon):\mathcal{C} \to \mathcal{D} では余結合律*1が成立します。準マルコフ余モナドの計算（「準マルコフ余モナドの計算と記述の方法」参照）で必要になるので、余結合律を一般化した法則を導入します。 \newcommand{\I}{ \mathrm{I} } \newcommand{\id}{\mathrm{id} } \newcommand{\cat}[1]{ \mathcal{#1} } \newcommand{\In}{ \text{ in } } \newcommand{\oplax}{\mathrm{oplax} } \newcommand{\BinTree}{\mathrm{BinTree} } \newcommand{\width}{\mathrm{width} } \newcommand{\LSw}{\mathrm{LSw} } \newcommand{\RSw}{\mathrm{RSw} } \newcommand{\Ev}{\mathrm{Ev} } \newcommand{\gcoM}{\bar{\boldsymbol{\delta}} } \newcommand{\oast}{\circledast }

内容：

二分木とモノイド圏

次の3種類の記号を考えます。

  1. 1, 2, 3, \cdots という番号
  2. \bullet という黒丸記号
  3. (\:) 左丸括弧と右丸括弧

黒丸を二項演算子記号と考えて、括弧のバランスがとれた記号列、例えば (1\bullet 2), ( (1\bullet 2)\bullet(3\bullet 4) ) などは二分木〈二進木 | binary tree〉のテキスト表現と考えられます。以下、記号列と二分木をほとんど同一視します。

二分木の葉〈リーフ〉として出現する番号は、（記号列表現でみて）必ず左から右に 1, 2, 3, \cdots と増えるとします。番号の葉がn個なら、黒丸のノードは(n - 1)個あります。n \ge 2 です。このような二分木全体の集合を \BinTree とします。特に、葉がn個である二分木の集合を \BinTree_n \text{ where }n \ge 2 とします。

\cat{C} をモノイド圏とします。t\in \BinTree_n と (A_1, \cdots, A_n)\in |\cat{C}|^n に対して、\cat{C} の対象 t_\cat{C}(A_1, \cdots, A_n) を次のように定義します。

  1. t の黒丸の出現を、モノイド圏 \cat{C} のモノイド積 \otimes = \otimes_\cat{C} で置き換える。
  2. t の葉 i\: (1\le i \le n) の出現を、モノイド圏 \cat{C} の対象 A_i で置き換える。
  3. モノイド積を計算することにより \cat{C} の対象を求める。

例を挙げると：

  1. t = (1\bullet 2) のとき、t_\cat{C}(A_1, A_2) は A_1 \otimes_\cat{C} A_2 を計算して得られる。
  2. t = ( (1\bullet 2)\bullet(3\bullet 4) ) のとき、t_\cat{C}(A_1, A_2, A_3, A_4) は (A_1 \otimes_\cat{C} A_2) \otimes_\cat{C} (A_3\otimes_\cat{C} A_4) を計算して得られる。

モノイド圏 \cat{C} が前もって決まっているときは、下付きの \cat{C} は省略します。例えば、t(A_1, A_2) = A_1 \otimes A_2 。

二分木の半オペラッド構造

二分木の全体 \BinTree には置換演算〈代入演算 | substitution {operation}?〉を定義できます。置換演算はオペラッドの結合演算の類似物とみなせます。オペラッドについては以下の過去記事に説明があります。

二分木の場合は、オペラッドと違って単位〈恒等〉に相当するモノはありません。半オペラッド（単位を持たないオペラッド）構造と言えるでしょう*2。

二分木の葉の個数を“幅”と呼び、\width(t)\text{ for }t\in \BinTree と書きます。\width : \BinTree \to {\bf N} という写像になります。

s, t\in \BinTree と 1\le i \le \width(t) に対して、t[s/i] という二分木を次のように定義します。

  1. 二分木 t の葉 i を、二分木 s で置き換える。
  2. 葉の番号を 1, 2, \cdots, \width(t) + \width(s) - 1 になるように振り直す。

例を計算してみます。

\quad (1\bullet 2)[(1\bullet 2)/2]\\ = (1\bullet (2\bullet 3))\\ \:\\ \quad ( (1\bullet 2)\bullet 3)[(1\bullet 2)[(1\bullet 2)/2 ] /3 ]\\ = ( (1\bullet 2)\bullet 3)[(1\bullet (2\bullet 3)) /3 ]\\ = ( (1\bullet 2)\bullet (3\bullet (4\bullet 5)) )

この置換演算は、接ぎ木〈grafting〉とも言えます。オペラッドに関する標準的記法では、t \circ_i s と書きます。同時に複数の箇所を置換するときは次のように書きます。

\quad t[u/i, v/j] \text{ where } 1\le i, j\le \width(t),\; i \ne j

ブラケットなかに入る置換指示の並びは置換リスト〈substitution list〉と呼びます。置換リストが空の場合は何もしないことを意味します。

同時置換は、一箇所だけの置換の繰り返しで表現できるので、基本となるのは一箇所の置換 t[s/i] = t\circ_i s です。

特別な置換演算としてペアリングがあります。

\quad s \triangle t := (1\bullet 2) [s/1, t/2]

ペアリングは (\triangle):\BinTree \times \BinTree \to \BinTree という二項演算になりますが、結合的でも単位的でもありません。

二分木の変形

この節の内容は、以下の過去記事の抜粋要約になります。

上記過去記事で、二分木の基本変形〈elementary {transformation | rewrite | deformation | move}〉を絵に描いています。

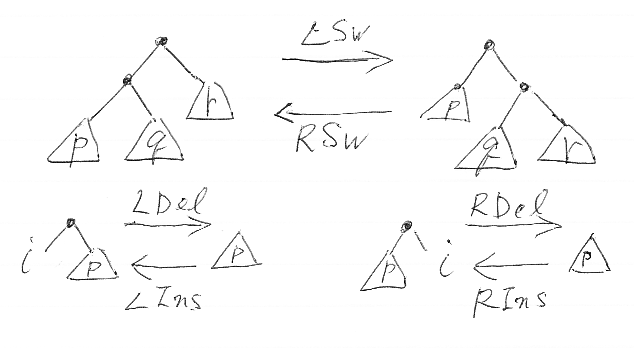
今回は、上段にある \LSw, \RSw （左からのスイッチと右からのスイッチ）という基本変形*3だけを使うので、下段の変形は無視してください。p, q, r などは部分木〈サブツリー〉を表し、葉であってもかまいません。

上の図は、二分木のトップレベルに変形を施していますが、部分木に対して \LSw, \RSw を適用してもかまいません。トップレベルに対する基本変形と、部分木に対する基本変形をあわせて単純変形〈simple {transformation | rewrite | deformation | move}〉と呼びます。

さらに、単純変形を何回か引き続き実行する操作を二分木の変形〈{transformation | rewrite | deformation | move}〉と呼びます。ここで考えている“変形”は、基本変形である \LSw, \RSw から生成されるものに限ります。

t\in \BinTree のとき、なんらかの変形 \beta を t に施して得られる二分木を t^\beta と書くことにします。変形自体は \beta: t \rightsquigarrow t^\beta と書きます。波矢印を見たら、二分木の変形だと判断してください。この書き方で基本変形を書くと次のようになります。

\quad \LSw : ( (1\bullet 2)\bullet 3) \rightsquigarrow (1\bullet (2\bullet 3)) \\ \quad \RSw : (1\bullet (2\bullet 3)) \rightsquigarrow ( (1\bullet 2)\bullet 3)

二分木を u = t[s/i] と書くと、変形のトップレベルへの作用やサブツリー（サブレベルのツリー）への作用を次のように書けます。

\quad u \rightsquigarrow t^\beta[s/i ] \text{ where }\beta:t \rightsquigarrow t^\beta \\ \quad u \rightsquigarrow t[s^\gamma/i ] \text{ where }\gamma:s \rightsquigarrow s^\gamma

二分木の変形 \beta: t \rightsquigarrow t^\beta があると、モノイド圏 \cat{C} の射が自然に決まります。

\quad t(A_1, \cdots, A_n) \to (t^\beta)(A_1, \cdots, A_n) \In \cat{C}

この射は、二分木 t と二分木の変形 \beta と対象のリスト (A_1, \cdots, A_n) から決まるので、\Ev(t, \beta, (A_1, \cdots, A_n)) と書きます。\Ev は evaluation〈評価〉からです。

\quad \Ev(t, \beta, (A_1, \cdots, A_n)) : t(A_1, \cdots, A_n) \to (t^\beta)(A_1, \cdots, A_n) \In \cat{C}

ちょっと細工すると、\Ev を関手とみなすことが出来ますが、今はこれ以上触れません。「ツリー書き換え系とマックレーンの一貫性定理」を参照してください。

反ラックス・モノイド関手の一般余乗法

F = (F, \delta, \varepsilon):\cat{C} \to \cat{D} が反ラックス・モノイド関手のとき、その余乗法〈comultiplication〉は、次のような射の族として書けます。

\quad \delta_{A, B}:F(A\otimes B) \to F(A)\otimes F(B) \In \cat{D} \text{ for }A, B\in |\cat{C}|

二分木を t := (1\bullet 2) \in \BinTree とすると、余乗法のプロファイル（域と余域の仕様）は次のようにも書けます。

\quad F(t(A, B)) \to t(F(A), F(B)) \In \cat{D}

別な二分木を選んで、例えば t = (1\bullet (2\bullet 3)) とすると、次のプロファイルが得られます。

\quad F(A\otimes (B\otimes C) ) \to F(A)\otimes (F(B)\otimes F(C)) \In \cat{D}

余乗法の組み合わせにより、すぐ上のプロファイルの射が得られます。具体的には次の射です。

\quad \delta_{A, B\otimes C}; (\id_{F(A)} \otimes \delta_{B, C}):F(A\otimes (B\otimes C) ) \to F(A)\otimes (F(B)\otimes F(C)) \In \cat{D}

「準マルコフ余モナドの計算と記述の方法」で導入した行列形式記法を使えば次のように書けます。

\begin{bmatrix} &F(A\otimes (B\otimes C))& \\ &\delta& \\ F(A) &|& F(B\otimes C) \\ \id &|& \delta \\ F(A) &|& F(B) \otimes F(C)\\ \end{bmatrix}

さて、\delta_{A, B} と \delta_{A, B\otimes C}; (\id_{F(A)} \otimes \delta_{B, C}) 、その他類似の射達を一挙に一様に扱うために、次の記法を導入します。

\quad \gcoM_{t, (A_1, \cdots, A_n)}:F(t(A_1, \cdots, A_n)) \to t(F(A_1), \cdots, F(A_n))\In \cat{D}

\gcoM_{t, (A_1, \cdots, A_n)} は、二分木 t と (A_1, \cdots, A_n) \in |\cat{C}|^n \text { where }n = \width(t) で決まる一般化された余乗法です（定義は後）。この記法を使うと、次のように書けます。

\quad \delta_{A, B} =: \gcoM_{(1\bullet 2), (A, B)} \\ \quad \delta_{A, B\otimes C}; (\id_{F(A)} \otimes \delta_{B, C}) =: \gcoM_{(1 \bullet (2\bullet 3) ), (A, B, C)}

\gcoM_{t, (A_1, \cdots, A_n)} の定義を、t = ( (1\bullet 2)\bullet (3\bullet4) ),\; (A_1, \cdots, A_n) = (A, B, C, D) の場合を例に説明します。

t は二分木ですが、 \gcoM_{t, (A_1, \cdots, A_n)} は t と“同じ形状”のストライプ図で定義されます。次の絵をみてください。

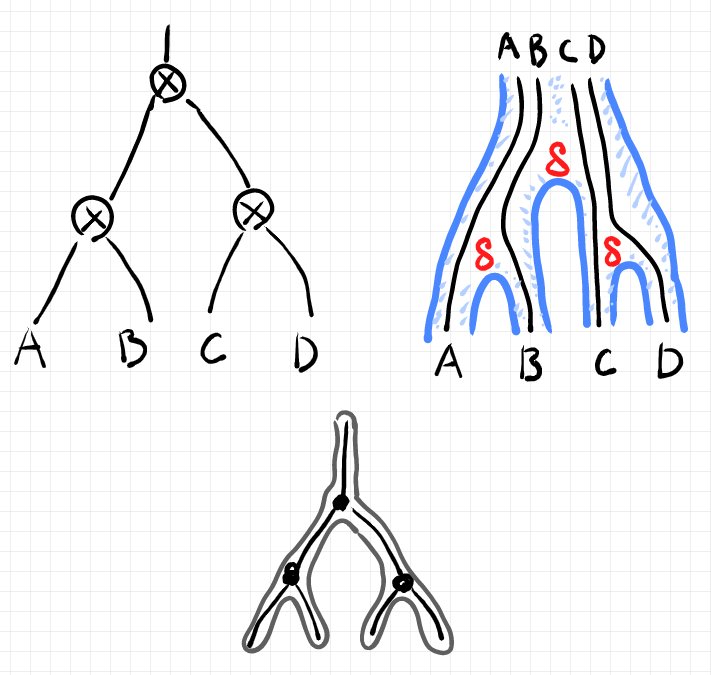
左上が t(A_1, \cdots, A_n) = ( (1\bullet 2)\bullet (3\bullet4) )(A, B, C, D) = (A\otimes B)\otimes (C\otimes D) を表す二分木です。右側が“同じ形状”のストライプ図です。「同じ形状」とは何かを具体的に言えば：

  • t の \bullet（または t(A_1, \cdots, A_n) の \otimes）の位置に余乗法 \delta が置かれたツリーが、 \gcoM_{t, (A_1, \cdots, A_n)} のストライプ図の形状となる。

上の絵の下側のツリーは、形状だけを取り出したツリーです。二分木としての ( (1\bullet 2)\bullet (3\bullet4) ),\; (A\otimes B)\otimes (C\otimes D) の形状、そして \gcoM_{t, (A_1, \cdots, A_n)} のストライプ図の形状と同じです。

念のため、\gcoM_{( (1\bullet 2)\bullet (3\bullet4) ), (A, B, C, D)} を行列形式記法で書くと次のようになります。

\quad \gcoM_{( (1\bullet 2)\bullet (3\bullet4) ), (A, B, C, D)} \\ = \begin{bmatrix} &F( (A\otimes B)\otimes (C\otimes D) )& \\ &\delta& \\ F( A\otimes B) &|& F(C\otimes D) \\ \delta &|& \delta \\ F(A)\otimes F(B) &|& F(C) \otimes F(D) \\ \end{bmatrix}

以上は、絵図を利用した直感的な説明でしたが、一般余乗法〈generic comulitplication〉 \gcoM_{t, (A_1, \cdots, A_n)} の作り方はこれで明らかだと思います。一般余乗法のもっとハッキリとした定義は、二分木の帰納的構造に沿った構造帰納法を使います。

反ラックス・モノイド関手の一般余結合律

|\cat{C}|^n の要素 (A_1, \cdots, A_n) を \vec{A} と書くことにします。一般余乗法（の成分）は \gcoM_{t, \vec{A}} と短く書けます。また、関手 F:\cat{C} \to \cat{D} に対して、

\quad F\oast\vec{A} := (F(A_1), \cdots, F(A_n))\;\in |\cat{D}|

という記法も使います。\oast は、リストに対するfmap高階関数の中置演算子記号だと思えばいいです。つまり \mathrm{fmap}(F, \vec{A}) = F\oast\vec{A} 。

以上の記法で、一般余乗法とそのプロファイルは次のように簡略に書けます。

\quad \gcoM_{t, \vec{A}}: F(t(\vec{A})) \to t(F\oast\vec{A}) \In \cat{D}

反ラックス・モノイド関手 F = (F, \delta, \varepsilon):\cat{C} \to \cat{D} の一般余結合律〈generic associative law〉は、次の図式の可換性を主張します。

\require{AMScd} \forall t\in \BinTree_n.\\ \forall \vec{A}\in |\cat{C}|^n .\\ \forall \beta: t \rightsquigarrow t^\beta.\\ \begin{CD} F(t(\vec{A})) @>{F(\Ev(t, \beta, \vec{A}))}>> F(t^\beta(\vec{A})) \\ @V{\gcoM_{t, \vec{A}}}VV @VV{\gcoM_{t^\beta, \vec{A}}}V \\ t(F\oast\vec{A}) @>{\Ev(t, \beta, F\oast\vec{A}))}>> t^\beta(F\oast\vec{A}) \end{CD}\\ \text{commutative in }\cat{D}

次の特殊ケースを考えます。

  • t = ( (1\bullet 2)\bullet 3)
  • \vec{A} = (A, B, C)
  • \beta = \LSw : ( (1\bullet 2)\bullet 3) \rightsquigarrow ( 1\bullet(2 \bullet 3))

このとき、

  • t(\vec{A}) = (A\otimes B)\otimes C
  • t(F\oast\vec{A}) = (F(A)\otimes F(B))\otimes F(C)
  • t^\beta = ( 1\bullet(2 \bullet 3))
  • t^\beta(\vec{A}) = A\otimes (B\otimes C)
  • t^\beta(F\oast\vec{A}) = F(A)\otimes (F(B)\otimes F(C))
  • \Ev(t, \beta, \vec{A}) = \alpha_{A, B, C}: (A\otimes B)\otimes C \to A\otimes (B\otimes C)
  • \Ev(t, \beta, F\oast\vec{A}) = \alpha_{F(A), F(B), F(C)}: (F(A)\otimes F(B))\otimes F(C) \to F(A)\otimes (F(B)\otimes F(C))

この状況での可換図式は次のようになります。

\require{AMScd} \begin{CD} F( (A\otimes B)\otimes C ) @>{F(\alpha_{A, B, C}) }>> F( A\otimes (B\otimes C) )\\ @V{\gcoM_{t, \vec{A}}}VV @VV{\gcoM_{t^\beta, \vec{A}}}V \\ (F(A)\otimes F(B))\otimes F(C) @>{\alpha_{F(A), F(B), F(C)} }>> F(A)\otimes (F(B)\otimes F(C)) \end{CD}\\ \text{commutative in }\cat{D}\\ \text{ where }\\ \quad \gcoM_{t, \vec{A}} = \delta_{A\otimes B, C};(\delta_{A, B} \otimes \id_{F(C)})\\ \quad \gcoM_{t^\beta, \vec{A}} = \delta_{A, B\otimes C};(\id_{F(A)} \otimes \delta_{B, C})

これは、反ラックス・モノイド関手の余結合律そのものです。

念のために、上記の可換図式をストライプ図の等式で描いてみます。

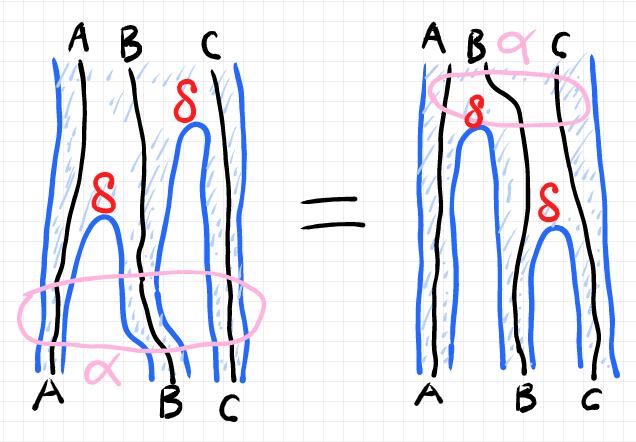
さらに、行列形式記法の等式で書くと次のようになります。

\begin{bmatrix} &F( (A\otimes B) \otimes C)& \\ &\delta& \\ F(A\otimes B) &|& F(C)\\ \delta &|& \id \\ F(A)\otimes F(B) &|& F(C) \\ &\alpha& \\ F(A) &|& F(B)\otimes F(C)\\ \end{bmatrix} = \begin{bmatrix} &F( (A\otimes B) \otimes C)& \\ &F(\alpha)& \\ &F( A\otimes (B \otimes C) )& \\ &\delta& \\ F(A) &|& F(B\otimes C)\\ \id &|& \delta \\ F(A) &|& F(B)\otimes F(C) \\ \end{bmatrix}

一般余結合律の事例

反ラックス・モノイド関手の一般余結合律は、特殊な場合として余結合律を含むことがわかりました。余結合律を仮定して一般余結合律を証明するのは組み合わせ的・帰納的議論になり面倒で退屈なので割愛し、もうひとつの事例を出します。

次のケースを考えます。

  • t = ( ( (1\bullet 2)\bullet 3)\bullet 4)
  • \vec{A} = (A, B, C, D)
  • \beta :( ( (1\bullet 2)\bullet 3)\bullet 4) \rightsquigarrow ( (1\bullet 2)\bullet (3\bullet 4) )

このとき、

  • t(\vec{A}) = ( (A\otimes B)\otimes C)\otimes D
  • t(F\oast\vec{A}) = ( (F(A)\otimes F(B))\otimes F(C))\otimes F(D)
  • t^\beta = ( (1\bullet 2)\bullet (3\bullet 4) )
  • t^\beta(\vec{A}) = (A\otimes B)\otimes (C\otimes D)
  • t^\beta(F\oast\vec{A}) = ( F(A)\otimes F(B))\otimes (F(C)\otimes F(D))
  • \Ev(t, \beta, \vec{A}) = \alpha_{A\otimes B, C, D}: ( (A\otimes B)\otimes C)\otimes D \to (A\otimes B)\otimes (C \otimes D)
  • \Ev(t, \beta, F\oast\vec{A}) = \alpha_{F(A)\otimes F(B), F(C), F(D)}: ( (F(A)\otimes F(B))\otimes F(C))\otimes F(D) \to (F(A)\otimes F(B))\otimes (F(C)\otimes F(D))

この状況での可換図式は次のようになります。

\require{AMScd} \begin{CD} F( ( (A\otimes B)\otimes C)\otimes D ) @>{F(\alpha_{A\otimes B, C, D}) }>> F( (A\otimes B)\otimes (C\otimes D) )\\ @V{\gcoM_{t, \vec{A}}}VV @VV{\gcoM_{t^\beta, \vec{A}}}V \\ ( (F(A)\otimes F(B))\otimes F(C))\otimes F(D) @>{\alpha_{F(A)\otimes F(B), F(C), F(D)} }>> (F(A)\otimes F(B))\otimes (F(C)\otimes F(D)) \end{CD}\\ \text{commutative in }\cat{D}\\ \text{ where }\\ \quad \gcoM_{t, \vec{A}} = \delta_{A\otimes B\otimes C, D};(\delta_{A\otimes B, C} \otimes \id_{F(D)}) ; (\delta_{A, B}\otimes \id_{F(C)} \otimes \id_{F(D)} ) \\ \quad \gcoM_{t^\beta, \vec{A}} = \delta_{A\otimes B, C\otimes D};( \delta_{A, B}\otimes \delta_{C, D} )

我々の目的である準マルコフ余モナドの計算で必要になるのは、幾つかの個別具体ケースで、ほんとに一般的な余結合律が必要なわけではありません。一方で、一般化を推し進める方向では、余単位律も含めた一般化も欲しくなります。これらの話題はまた次の機会に。

*1:余結合律に類似の法則と言うべきでしょうが、ここでは単に余結合律と呼ぶことにします。

*2:二分木の全体をオペラッドに仕立てることは出来ますが、意外とめんどくさいので、今回は半オペラッドでよいとします。

*3:LとRだけでは分かりにくいので \mathrm{LRSw},\mathrm{RLSw} とすべきかも知れません。