モノイド対象と単体的対象 - 檜山正幸のキマイラ飼育記 (はてなBlog)

「複体、複体、複体 … なんとかしてくれ！」を書いているときにふと思ったことがあるんですが、横道にそれるので書きませんでした。そのことをこの記事で書きます。

ふと思ったこととは、「圏C内のモノイド対象と、圏C内の単体的対象は酷似した概念だなー」。モノイド対象と単体的対象が酷似しているのなら、指標とモデルの理論（インスティチューション理論含む）と、ローヴェア理論（ちゃんと言うと、「ローヴェア理論」の理論）と、形状圏を使ったホモロジー／コホモロジーが扱っているモノ達は、酷似しているのでしょう、おそらく。

書き方に関する注意：ある言葉の同義語がある場合は、山形括弧（'〈'と'〉'）で囲んで示します。

内容：

モノイド対象
モノイドの指標
ローヴェア圏
モノイドの指標のローヴェア圏
ローヴェア圏の別な構成法
モノイド対象再度
指標とモデルの圏に関するネーミング・コンベンション
単体形状圏
次元がズレている！
おわりに

モノイド対象

モノイド〈monoid〉とは、集合Aと、二項演算 (*) = (-*-) = λ(x, y)∈A×A.(x*y) : A×A→A と、特定の要素 e∈A からなる構造です。二項演算(*)と要素eは、結合律と左右の単位律を満たします。

結合律： (x*y)*z = x*(y*z)
左単位律： e*x = x
右単位律： x*e = x

単なる集合Aの代わりに、順序集合 (A, ≦) を台〈underlying thing〉にした場合は順序モノイド〈ordered monoid〉が定義できます。順序モノイドでは、二項演算(*)が、順序(≦)と整合することが要求されます。

x ≦ x' かつ y ≦ y' ならば x*y ≦ x'*y'

自然数の普通の大小順序に足し算（あるいは掛け算）を考えると順序モノイドになります。非負実数係数の正方行列の集合に、成分ごとの順序から導かれる順序*1と行列の掛け算を考えると、非可換な順序モノイドになります。

Vが（R上の）ベクトル空間で、双線形な二項演算 (*):V×V→V と、特定の要素 e∈V がモノイドと同じ法則（結合律と左右の単位律）を満たすとき（R上の）代数〈多元環 | algebra〉と呼びます。双線形写像は、テンソル積 V $\otimes$ V からの線形写像とみてもいいので、(*):V $\otimes$ V→V とも書けます。V = End(W) = Vect_R(W, W) = (WからWへのR-線形写像全体のベクトル空間) とすると、Vは線形写像の結合を二項演算（掛け算）として代数〈多元環〉になります。

以上に挙げた、普通のモノイド、順序モノイド、代数〈多元環〉を統一的・総称的に扱いたいときは、“圏C内のモノイド対象”という概念が使えます。

普通のモノイドは、圏Set内のモノイド対象
順序モノイドは、圏Ord内のモノイド対象
（R上の）代数〈多元環〉は、圏Vect_R内のモノイド対象

実は、モノイド対象をホストする圏Cは、単なる圏ではなくてモノイド圏〈monoidal category〉です。Set, Ord, Vect_R は横着して書いてる、あるいは、次のような記号の乱用をしています。

Set = (Set, ×, 1)
Ord = (Ord, ×, 1)
Vect_R = (Vect_R, $\otimes$ , R)

上記乱用の右辺もまだ正確ではなくて、オーバーロード／略記をしています。

'×'は、集合の直積、または、順序集合の直積。
'1'は、特定された単元集合、または、特定された単元集合上の自明な順序集合。
' $\otimes$ 'は、実数体R上のテンソル積 $\otimes_\bf{R}$ 。
モノイド圏の結合律子、左単位律子、右単位律子は省略（律子に関しては「律子からカタストロフへ」を参照）。

普通のモノイドは、直積を備えた集合圏におけるモノイド対象ですが、他のモノイド圏内でもモノイド対象を考えることができます。

モノイドの指標

モノイド対象を構文的に定義するために指標〈signature〉を使いましょう。

signature Monoid {
 sort A
 operatiron (*):A×A→A
 operation e:1→A
 equation assoc:: ((*)×id_A);(*) ⇒ (id_A×(*));(*)
 equation lunit:: (e×id_A);(*) ⇒ id_A
 equation runit:: (id_A×e);(*) ⇒ id_A
}

いくつかの注意事項を：

指標と仕様の区別は決めてませんが、ここでは、指標内に法則も書いています。
(*) という書き方はHakell風です。「指標のパラメータ化とグロタンディーク構成」の最初のほうに、二項演算を'm'という記号で表した指標があります。
equation〈等式〉と書いてありながらイコール記号でなくて二重矢印を使っている理由は：
1. 律子を省略しているので、正確にイコールではない。
2. 1-射である演算〈operation〉を一重矢印、2-射である等式を二重矢印と揃えたかった。

上に挙げた指標は、一般的・総称的です。特定の圏ごとに具体化してみます。

集合圏において具体化

signature Monoid {
 sort A in Set
 operatiron (*):A×A→A in Set
 operation e:1→A in Set
 equation assoc:: ((*)×id_A);(*) ⇒ (id_A×(*));(*) in Set
 equation lunit:: (e×id_A);(*) ⇒ id_A in Set
 equation runit:: (id_A×e);(*) ⇒ id_A in Set
}

AはSetの対象、つまり集合である。
二項演算(*)はSetの射、つまり写像である。
'×'は集合の直積を表す。
1は単元集合を表す。
eは単元集合1からの射（写像）とみなす。単元集合からの写像は要素と同じこと。
等式は、写像の等しさと解釈する。

順序集合の圏において具体化

signature OrderedMonoid {
 sort A in Ord
 operatiron (*):A×A→A in Ord
 operation e:1→A in Ord
 equation assoc:: ((*)×id_A);(*) ⇒ (id_A×(*));(*) in Ord
 equation lunit:: (e×id_A);(*) ⇒ id_A in Ord
 equation runit:: (id_A×e);(*) ⇒ id_A in Ord
}

AはOrdの対象、つまり順序集合である。
二項演算(*)はOrdの射、つまり順序を保存する写像である。
'×'は順序集合の直積を表す。
1は単元集合を台とする自明な順序集合を表す。
eは自明な順序集合1からの射（順序を保存する写像）とみなす。自明な順序集合からの順序を保存する写像は要素と同じこと。
等式は、順序を保存する写像の等しさと解釈する。

ベクトル空間の圏において具体化

signature Algebra {
 sort V in Vect_R
 operatiron (*):VV→V in Vect_R
 operation e:R→V in Vect_R
 equation assoc:: ((*)id_V);(*) ⇒ (idV(*));(*) in Vect_R
 equation lunit:: (eid_V);(*) ⇒ id_V in Vect_R
 equation runit:: (id_Ve);(*) ⇒ id_V in Vect_R
}

VはVect_Rの対象、つまり（R上の）ベクトル空間である。
二項演算(*)はVect_Rの射、つまり線形写像である。
' $\otimes$ 'はベクトル空間のテンソル積を表す。
Rは実数体をベクトル空間とみなした自明な1次元ベクトル空間を表す。
eは自明な1次元ベクトル空間Rからの射（線形写像）とみなす。自明な1次元ベクトル空間からの線形写像は要素と同じこと。
等式は、線形写像の等しさと解釈する。

ローヴェア圏

モノイドの指標を、特定の圏（ここでは、Set、Ord、Vect_R）内で“実現”することにより、各圏内のモノイド対象が得られます。モノイド対象は、モノイドの指標から圏Cへの関手と捉えます。しかし、前節に書き下したテキスト形式だと、「指標が圏である」とは思えないでしょう。

テキストとして書き下した指標には、色々と余分で恣意的な情報が含まれます。例えば：

ソート〈sort〉の名前は 'A' か 'V' か。はたまた、'X' がいいのではないか。
モノイド積の記号は、集合圏に合わせて'×'がいいのか、テンソル積の記号' $\otimes$ 'がいいのか。はたまた、見慣れない記号' $\boxplus$ 'がいいのではないか。
二項演算の記号は、中置演算子をHaskell風に書いた'(*)'がいいのか、一文字の'm'がいいのか。はたまた、'mul'のような綴りがいいのではないか。
などなど … …

構文を決めるとは、こういう、どうでもいい選択に決着を付けることです*2。が、モノイド対象（モノイドの指標のモデル）を考えるとき、どうでもいい構文（記号・書き方の決め事）の影響を受けるのは避けたいです。そこで、構文の定義をテキストで書き下した指標をもとに、そのローヴェア圏を作ります。

ローヴェア圏〈Lawvere category〉は、通常はローヴェア理論〈Lawvere theory〉と呼ばれます（https://ncatlab.org/nlab/show/Lawvere+theory 参照）が、紛らわしい呼び名なのでローヴェア圏にします。ちなみに、「用語のバリエーション記述のための正規表現 // ウンザリする例」で、「ローヴェア圏」の（あり得る）別名を60個列挙しています。

さて、ローヴェア圏とは次のような圏Lです。

Lは、直積（デカルト積）を持つ小さな圏である。
Lの対象集合は、自然数の集合と同型である。
適切な同型写像 N→|L| を選ぶと、Lの直積は、Nの足し算で表現できる。

上記条件の「適切な同型写像」を φ:N→|L| とすると、φ(n) を [n] とか n とか略記します。この略記を使うと、3番目の条件は次のように書けます。

[n]×[m] = [n + m]

特に、[0] は直積の単位になります。Nと|L|の1：1対応を与える φ = [-] もローヴェア圏の構造の一部とみなすことにします。

2つのローヴェア圏 L, M のあいだの準同型関手 F:L→M とは、次のように、直積を厳密に保存する〈strictly preserving〉関手です。圏同型な2つのローヴェア圏は同一視します。

F([n]×[m]) = F([n])×F([m])

ローヴェア圏Lはデカルト圏（直積を持つ圏）なので、[n + m] = [n]×[m] に対して、射影 [n + m]→[n], [n + m]→[m] in L を持ちますが、そこまでは要求しないで、単なるモノイド圏でもいいと条件を緩めたローヴェア圏をモノイド・ローヴェア圏〈monoidal Lawvere category〉と呼ぶことにします*3。モノイド・ローヴェア圏のあいだの準同型関手は、厳密モノイド関手です。

指標のモデルは、指標に対応するローヴェア圏またはモノイド・ローヴェア圏のモデルと解釈できます。となると、指標からローヴェア圏を作り出す手順が必要になります。それは次節で述べます。

モノイドの指標のローヴェア圏

単ソート等式的指標〈single-sorted equational signature〉から、ローヴェア圏を作ることができます。が、一般的な手順を説明するのは面倒なので、我々の事例であるモノイドの指標から、対応するローヴェア圏を実際に作るだけにします。これから作るローヴェア圏は、本来のローヴェア圏（直積を持つ圏）ではなくてモノイド・ローヴェア圏ですが、モノイド・ローヴェア圏も単にローヴェア圏と呼んでしまいます。

モノイドの指標を再掲します。

signature Monoid {
 sort A
 operatiron (*):A×A→A
 operation e:1→A
 equation assoc:: ((*)×id_A);(*) ⇒ (id_A×(*));(*)
 equation lunit:: (e×id_A);(*) ⇒ id_A
 equation runit:: (id_A×e);(*) ⇒ id_A
}

記号 [n] で、Aをn個掛け合わせたモノを表すとします。

[n] = A× ... ×A （n個）

[1]はAのことで、[0]は1のことだとします。

二項演算 (*) の代わりに Y、要素のポインティング射 e の代わりに i を使います。なんで、'Y'と'i'なんだ？と訝〈いぶか〉しく思うでしょうが、これらの文字は“象形文字”として使います。象形文字とは、絵と似た形状の文字ということです。僕が愛用(?)している象形文字を挙げておきます。

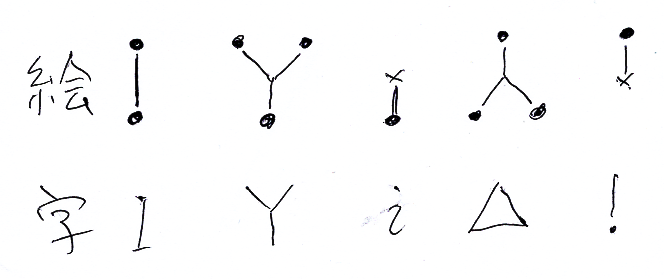
象形文字'I'は id_A を表します。さらに、[n] はドット'.'をn個並べて表現します。例えば、[2] = .. 、[3] = ... 、[0] は何もない空虚になります。これらの象形文字を使って指標を書き直すと：

signature Monoid {
 sort .
 operatiron Y: .. → .
 operation i: → .
 equation assoc:: (Y×I);Y ⇒ I×Y;Y
 equation lunit:: (i×I);Y ⇒ I
 equation runit:: I×i;Y ⇒ I
}

'×'を横並置、';'を縦並置として、等式的法則（結合律、左右の単位律）をアスキーアートで記述してみます。

... 　 ...
Y I 　 I Y
. . ⇒ . .
 Y  　  Y
 .  　  .

  . 　 .
i I 　 |
. . ⇒ I
 Y  　 |
 .  　 .

.   　 .
I i 　 |
. . ⇒ I
 Y  　 |
 .  　 .

アスキーアートじゃなくて、普通の絵で描くなら（あんまり代わり映えしない）：

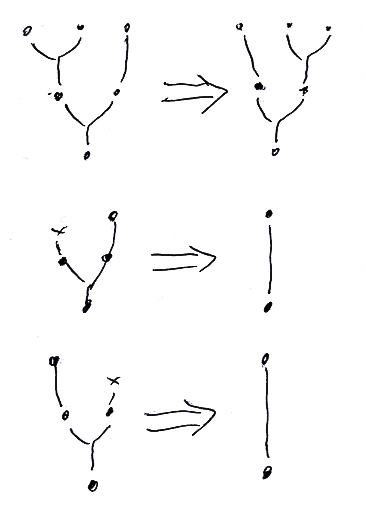
象形文字と絵により直感が得られたところで、モノイドの指標のローヴェア圏 Lawv(Monoid) を定義します。Lawv(Monoid) は厳密モノイド圏です。

mon = Lawv(Monoid) と置くとして：

|mon| = {[n] | nは自然数} $\cong$ N
monの射は、I, Y, i から横並置と縦並置で構成される“図形”の同値類。縦並置はテキストで書けないのでセミコロンで縦並置を表す。
同値類を作るときの同値関係は、結合律、左単位律、右単位律に相当する変形（上の絵の'⇒'で表現される描き換え）と、縦棒（何個かのIの縦並置）を縮める操作を何度かして同じ図形になるなら同値とする。
dom, cod は：
1. dom(Iの同値類) = [1], cod(Iの同値類) = [1]
2. dom(Yの同値類) = [2], cod(Yの同値類) = [1]
3. dom(iの同値類) = [0], cod(iの同値類) = [1]
射の結合は図形の縦並置。
恒等射は、id_[n] = (Iをn個横に並べた図形)
対象のモノイド積は [n] $\otimes$ [m] := [n + m]
射のモノイド積は図形の横並置
モノイド積の単位対象は [0]

ローヴェア圏の別な構成法

前節で述べた mon = Lawv(Monoid) = (モノイドの指標のローヴェア圏) は、絵を描けるので、直感的理解には向いています。が、直感的であるゆえに、なんかハッキリしない印象もあるでしょう。もっとハッキリしていて簡単な構成を紹介します。

まず、Ordは順序集合と順序を保存する写像の圏です（既に出ています）。順序を保存する写像は単調写像〈{monotone | monotonic} {map | mapping | function}〉とも呼びます。TotOrdは、全順序集合〈{total | linear} ordered set〉の圏だとします。TotOrdは、Ordの充満部分圏です。さらに、有限集合が台である全順序集合の圏をFinTotOrdとします。FinTotOrdは、TotOrdの充満部分圏です。

一般に、圏Cの部分圏Sが、Cの骨格〈skeleton〉だとは、Sが骨格的であり、CとSが圏同値になることです。より詳しくは：

FinTotOrdの標準骨格〈canonical skeleton〉を、CanSkelFinTotOrd と…、いやっ、綴りを省略しても長すぎるので、CSFTOとします。CSFTOを具体的に記述しましょう。

CSFTOの対象は、自然数の区間 {0, 1, ..., n} に通常の順序を考えた有限全順序集合。空集合 {}、単元集合 {0} もCSFTOの対象。
射は、単調写像。
射の結合と恒等射は、写像の結合と恒等写像。

前節と同じ記号 [n] を次の意味で再定義します。

[0] = {}
[1] = {0}
[2] = {0, 1}
[n] = {0, ..., n-1} = {k∈N | 0≦ k <n}

CSFTOは、モノイド積を [n] $\otimes$ [m] := [n + m] と定義してモノイド・ローヴェア圏になります。モノイド・ローヴェア圏Mの定義は次のようでした。

Mは、モノイド積を持つ小さな圏である。
Mの対象集合は、自然数の集合と同型である。
適切な同型写像 N→|L| を選ぶと、Lのモノイド積は、Nの足し算で表現できる。

CSFTOはこれらの条件を満たします。

前節で、絵を使って定義した“モノイドの指標のローヴェア圏”は、CSFTOと同型です。象形文字 I, Y, i に対応する単調写像を具体的に書き下します。絵ではなくて写像〈関数〉なので、記述のために番号（上付き・下付き添字）が必要です。

I_n:[n]→[n]
For k∈[n], I_n(k) := k
Y_n^j:[n+1]→[n] （0≦ j <n）
For k∈[n], Y_n^j(k) := if (k ≦ i) then k else (k - 1)
i_n^j:[n-1]→[n] （0≦ j <n）
For k∈[n], i_n^j(k) := if (k < j) then k else (k + 1)

これらの単調写像達（の一部）を絵に描いてみると、次のよう。

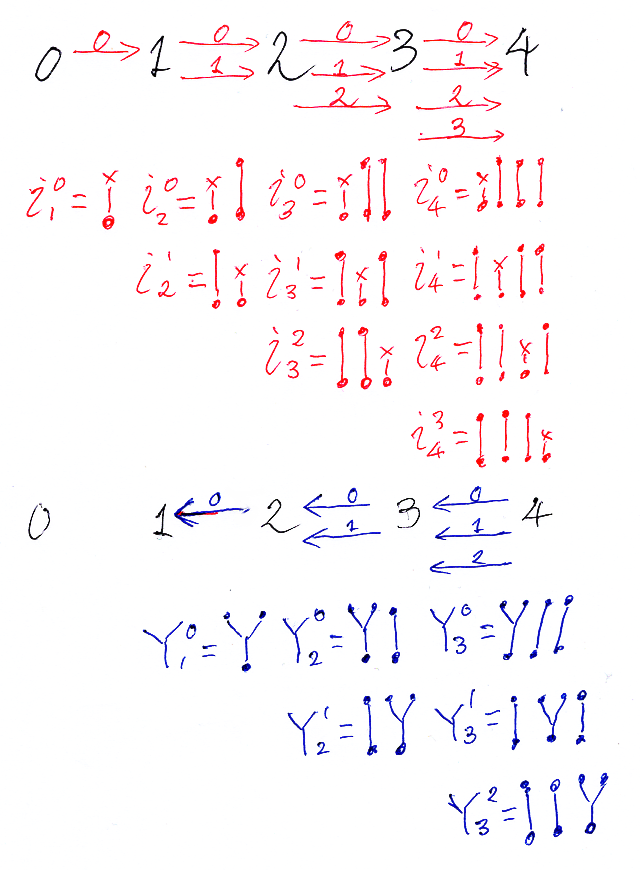
写像 Y_n^j では、出力値が j のところでだけ値の衝突〈double hit | collision〉が発生します。写像 i_n^j では、出力値が j のところでだけ入力値がありません（逆像が空集合）。I₀は[0]（空集合）の恒等写像、i₁⁰は空集合から単元集合への唯一の写像です。

CSFTOの任意の射（つまり、単調写像）は、I_n, Y_n^j, i_n^j を組み合わせれば作ることができます。これを実際に確認するのは良い練習問題です。

前節の mon = Lawv(Monoid) と、この節のCSFTOは、定義の仕方はまったく違いますが、同型な圏です。片方は人間の図形的な直感に訴え、もう一方はアルゴリズム的で計算機で計算することも出来ます。

モノイド対象再度

テキストとして書かれた指標は、インターフェイスと制約に関する記述です。そのまま直接に、圏論的マシーナリーへとインプットは出来ません。が、指標から作ったローヴェア圏は圏なので、圏論の遡上に載せることが出来ます。

MonCAT を、小さくないかも知れないモノイド圏の圏とします。モノイド関手はいっぱい種類がありますが、ここではタイト・モノイド関手を射にします。モノイド関手の種類も明示して MonCAT^tight とします。MonCAT^tight は、モノイド圏の直積をモノイド積として、それ自身モノイド圏になります。そして、内部ホム hom_MonCAT^tight(C, D) を持ちます。この内部ホム〈指数対象〉を [C, D] と略記します。

Lをモノイド・ローヴェア圏としましょう。もちろん、L∈|MonCAT^tight| です。C∈|MonCAT^tight| とします。すると、内部ホム [L, C] を作れます。この内部ホム圏が、ローヴェア圏LのCにおけるモデルの圏です。次の記号を使います。

Model(L, C) := [L, C]

Model(L, C) は関手圏なので、射は自然変換です。Cのモノイド構造を受け継いでモノイド圏になります。

ローヴェア圏Lとして、特に L := mon = Lawv(Monoid) としたとき、Model(mon, C) が、Cにおけるローヴェア圏monのモデルの圏です。圏 Model(mon, C) の対象が、C内の〈Cにおける〉モノイド対象〈monoid object〉です -- やっと、モノイド対象を正式に（ちょっと大げさな道具で）定義できました。

Σをなんらかの指標だとするとき、記号の乱用で、

Model(Σ, C) := Model(Lawv(Σ), C)

と定義します。今の例だと、

Model(Monid, C) = Model(Lawv(Monoid), C) = Model(mon, C)

Cを特定した場合は次のようになります。

Model(Monid, Set) = Mon = (普通のモノイドの圏)
Model(Monid, Ord) = OrdMon = (順序モノイドの圏)
Model(Monid, Vect_R) = Alg_R = (R上の代数の圏)

指標とモデルの圏に関するネーミング・コンベンション

話のついでに、指標とそのモデルの圏に名前を付けるときの規則〈コンベンション〉を述べておきます。僕の個人的規則ですが、規則があれば命名の負担が軽くなります。

指標名に対して、ニックネームを決めます。ニックネームは指標名そのままでも、短縮名でもかまいませんが、小文字始まりとします。例えば、

Monoid のニックネームは mon
Group のニックネームは grp
CommutativeGroup のニックネームは ab
CommutativeRing のニックネームは crng

指標に対応するローヴェア圏の名前は、ニックネームをそのまま使います。

Lawv(Monoid) = mon
Lawv(Group) = grp
Lawv(CommutativeGroup) = ab
Lawv(CommutativeRing) = crng

モデルの圏の名前は、ローヴェア圏の名前（＝ニックネーム）の最初を大文字にした名前を関手の名前として使って書きます。

Model(mon, C) = Mon(C)
Model(grp, C) = Grp(C)
Model(ab, C) = Ab(C)
Model(crng, C) = CRng(C)

C = Set の場合は、関手の名前を太字にして圏の名前とします。

Mon(Set) = Mon
Grp(Set) = Grp
Ab(Set) = Ab
CRng(Set) = CRng

こういう規則は、常に守れるとは限りませんが、原則は決めておくほうがいいでしょう。

単体形状圏

CSFTOから空集合を取り除いた圏をCSFTO+とします。末尾のプラスは、何かを加えた意味ではなくて、非空集合≒非ゼロ集合≒正の集合という連想からです。対象 [0] を取り除いたので、[0] から出る射もなくなります（[0]に入る射は I₀ 以外はもともと存在しません）。

「複体、複体、複体 … なんとかしてくれ！」に出てきた単体圏〈単体形状圏〉Sの標準的な定義は次です*4。

S := CSFTO+^op

反対圏における射を、右肩に'op'を付けて表すことにして、Sの面作用素は、(i_n^j)^op:[n]→[n-1] 達です。そして、Sの退化作用素は (Y_n^j)^op:[n]→[n+1] 達です。僕は、(i_n^j)^op = !_n^j, (Y_n^j)^op = Δ_n^j と書くことが多いですが、名前や番号の付け方は人により変わります*5。Sの定義から、余単体圏〈余単体形状圏〉S^op はCSFTO+そのものになります。

モノイドのローヴェア圏 mon = CSFTO （同一視してしまいましょう）と、余単体圏 S^op = CSFTO+ はほとんど同じものです。空集合の有り無ししか違いがありません。

CSFTO, CSFTO^op, CSFTO+, CSFTO+^op, から集合圏への関手圏を考えると次のようになります*6。

[CSFTO, Set] = Model(mon, Set) = (モノイドの圏)
[CSFTO^op, Set] = Model(comon, Set) = (コモノイドの圏)
[CSFTO+, Set] = S^op.Set = (余単体的集合の圏)
[CSFTO+^op, Set] = S.Set = (単体的集合の圏)

つまり、モノイド／余単体的集合／コモノイド／単体的集合という概念は酷似しています。モノイド以外の指標や、単体圏以外の形状圏においても、同様な現象は起きるのでしょうか？指標とモデルの理論と形状圏を使った方法（S的方法）には、なにかしらの内在的関係があるのでしょうか？

次元がズレている！

最後に、ひとつ注意をしておきます。ローヴェア圏の対象を [0], [1], [2], ... のように書きました。CSFTO においては、[0] = {}, [1] = {0}, [2] = {0, 1} でした。

ところが！単体圏／余単体圏では、通常次の定義を採用します。

[0] = {0}
[1] = {0, 1}
[2] = {0, 1, 2}
[n] = {0, ..., n} = {k∈N | 0≦ k ≦ n}

次元（番号）の数え方がズレているのです。空集合が必要なときは、

[-1] = {}

と、空集合の次元を -1 とします。

1だけシフトして考えればいいのですが、けっこうなフラストレーションになります。

おわりに

“指標とそのモデル”という概念は次のように一般化できます。

指標 → コンピュータッド
指標のローヴェア圏 → コンピュータッドが生成する最小で最厳密な圏
指標のモデル圏 → コンピュータッドから生成された圏（一般化ローヴェア圏）から、ターゲット圏（モデル達が棲む圏）への関手圏

“指標とそのモデル”は、「デカルト構造の無限タワー：怖がらずに登れ」で述べたような無限階層を作ります。モデルのターゲット圏が、メタ指標（例えば、モノイド圏の指標）により特徴付けられるので、ひとつ上の階層の存在が仮定され、その階層も同様にひとつ上の階層の存在が仮定され、……

モノイドの指標や単体形状圏は、このような無限階層のなかで一番扱いやすい部分を形成しているように思えます。扱いやすいけれども決して自明ではないところが魅力的です。

[追記]
この記事内に、幾つか「単体集合」という語がありました。「単体的集合」に置換しました。「的」の有無を気にしたくはないのですが、単体圏〈simplex category〉と単体的圏〈simplicial category〉では意味が変わるので、他の場合も"simplicial"なら「単体的」にします。が、いつでも「的」の有無を区別し続けるのは困難そうなので、そのうちイイカゲンになってしまいそうです。
[/追記]

*1:A ≦ B を、すべての成分で A_{j i} ≦ B_{j i} と定義することです。

*2:形式言語の構文を設計するときは、「どうでもいい選択に決着を付ける」ために、膨大な労力を使います。理論的にはどうでもいいからこそ、現実的にシリアスに考慮すべき点は多数あり、決定はとてもむずかしい作業となります。

*3:モノイド・ローヴェア圏と同様な概念の呼び名としては、PRO, PROPがあります。PROは対称性を仮定しないモノイド圏、PROPが対称モノイド圏バージョンのローヴェア圏です。また、クローンは複圏バージョンのローヴェア圏です。

*4:単体圏と余単体圏の定義が逆になることもあります。鬱陶しい話ですが、しょうがない。

*5:同一人物＝檜山のなかでも、気分で変えたりしてます。象形文字の観点からは退化作用素がΔですが、境界作用素∂の材料としての面作用素をδと書いたりします。

*6:単体的集合の変種として、添加単体的集合〈augmented simplicial set〉というモノがあります。添加単体的集合に条件を付けると、コモノイドの圏になります。もっとも、添加単体的集合の用途はコモノイドの圏を作ったりすることではないようですが。