先日書いた「双代数と双モノイド」という記事内で、双代数法則(biagebra laws)を示すために、次のような手描きの絵を載せました。
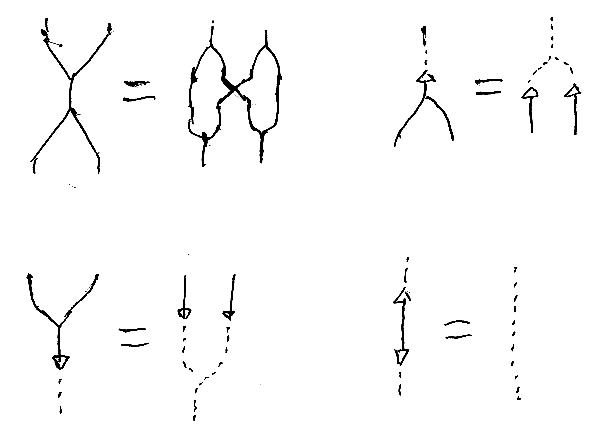
他にも、圏のなかで成立する等式的法則を描いた図は何度も使っています。でも、あっちこっちに散らばっていて参照には不便です。Categorical Tensor Network States (http://arxiv.org/abs/1012.0531) という論文に、代表的な等式の絵がコンパクトにまとまっていたので、切り取って貼り付けておきます。
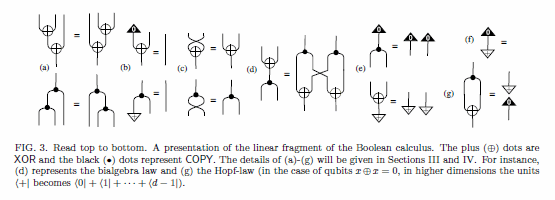
絵の下の説明にあるように、これはブール計算の線形なフラグメントに関する法則を列挙したものです。しかし、(後で注意するホップ法則を除いて)一般的な可換ホップ代数に関する法則だと理解してもかまいません。そのように解釈するとして、少し説明を加えます。
プラスの丸印がモノイド演算、上にとんがった黒三角をモノイド単位として、(+, 0) がモノイドになります。この絵では、演算は可換としているので +, 0 を使っています。一般的な状況では可換とは限らないモノイドを考えます。
黒丸が余モノイド余演算、下にとんがった白抜き三角を余モノイド余単位として、(・, +) が余モノイドになります。白三角のなかにもプラスが書き込んであるのは紛らわしいですね。僕は、余単位に ! をよく使います。
線の交差は対称(symmetry)を表します。つまり、これらの絵は対称モノイド圏のなかで解釈するわけです。
さて、法則を順に見ていくとして: (a)の上段は結合律(結合法則)、下段は余結合律です。(b)の上段は左単位律、下段は左余単位律です。演算/余演算の可換性/余可換性を仮定しているので、右単位律と右余単位律が省略されていますが、可換/余可換とは限らない一般的な状況では省略できません。そして(c)が、可換律と余可換律です。
(d), (e), (f) は、「双代数と双モノイド」で言及した双代数律(双代数法則)です。モノイドと余モノイド(代数と余代数)が混じったときの法則性ですね。(f)の左辺が何も書いてないのは間違いではありません。このことは「双代数と双モノイド」で注意しています。
最後の(g)はホップ律です。逆元の存在を主張しています。しかし、この絵では、x + x = 0 という特殊な状況を扱っているので、逆にする操作が描かれていません。通常は、逆元を作る(と解釈できる)対蹠(antipode)という操作を描きます。対蹠をSとすると次の絵になります(「ホップ代数の絵算 1:準備編」より。)。

これらの等式を基本的な書き換え(描き換え)規則とみなして、絵を変形していくのが絵算(pictorial/graphical/diagrammatic calculation)です。