先日、「n-圏とは何だろう」ってエントリーを書いたのですが、普通の圏でさえ浮世離れした印象があるのに、n-圏(高次圏)とかいわれても、「それ、食えないんでしょ?」という程度の反応になるのも無理もないですね。
でも実際は、圏やモナドの例がいくらでもあるのと同様に、n-圏の例もいくらでもあります。「n-圏とは何だろう」の冒頭で紹介したグループ・ブログThe n-Category Cafe を書いているメンバーは数理物理学者達で*1、場の量子論や重力理論に高次圏論を使ったアプローチを試みています。この現象世界そのものが、n-圏の具体例のひとつなのかもしれません。
とはいえ僕は、現象世界とn-圏の関係はサッパリわかりませんから、物理的な観点からの説明はできません。むしろ、現実とは離れたファンタジーとしてのn-圏のほうが、多少は説明できそうな気がします。という次第で、n-圏を、n次元までのモノ達(things)により構成される“架空の世界”として紹介します。
内容:
圏の定義を復習
「はじめての圏論 その第1歩:しりとりの圏」に、圏の実例と定義が書いてあります。もうちょっと堅苦しい定義は http://d.hatena.ne.jp/keyword/%b7%f7%cf%c0 にありますね。
Cが圏であるとき、Cの対象(object)の集合を Obj(C)、Cの射(morphism)の集合を Morph(C) と書いたりします*2。多くの場合、Obj(C)を|C|と書き、Morph(C)を表すのに記号Cを流用してしまいます。dom, cod, id などの写像も、それが圏Cに属するものであることをハッキリと示すには、domC, codC, idC とでも書かないといけないでしょう*3が、普通そこまでしません。A∈|C| に対するidの値は、通常、id(A) ではなくてidA と書きます。dom(f) = A, cod(f) = B であるfの全体は C(A, B) と書きます。
以上が標準的な記法です。しかし、この記法をn-圏に一般化するのは困難なので、次のような用語と記法を採用します。
- 対象を0-セルとも呼ぶ。
- 射を1-セルとも呼ぶ。
- 圏Cの対象(0-セル)の集合を C(0) と書く。
- 圏Cの射(1-セル)の集合を C(1) と書く。
- A, B∈C(0) に対して、dom(f) = A, cod(f) = B であるfの全体は C(1)(A, B) と書く。
右肩に付いた0と1は次元を表します。指数(累乗)と勘違いしないように括弧を付けておきました(慣れれば括弧は不要でしょう)。
さらに:
- A∈C(0) に対するidの値は、(idAではなく)id(A) と書く。
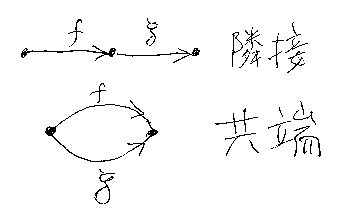
- f, g∈C(1) が、cod(f) = dom(g) のとき、fとgは隣接しているという。
- f, g∈C(1) が、dom(f) = dom(g) かつ cod(f) = cod(g) のとき、fとgは共端であるという*4。
隣接している1-セル(2本)と共端な1-セル(2本)を絵に描けば次のようになります。
3次元の多面体
我々は3次元の空間に棲んでいるので、圏の3次元版である3-圏を話題にしましょう。通常の圏は1-圏ですが、それは射が図形としては1次元的だからです。3-圏では、図形として3次元的な3-セルが登場します。3-セルを図示するば、なんらかの多面体になります。以下に多面体の例をいくつか挙げましょう。
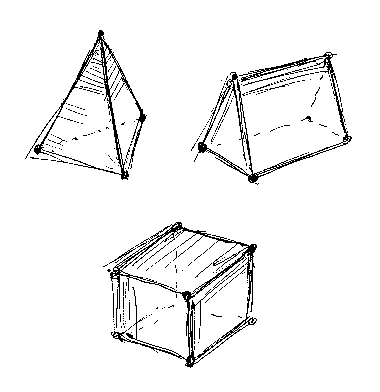
これらの多面体は、単に表面だけがあるのではなくて中身が詰まっているとします。つまり、紙を貼り合わせたようなものではなくて、煉瓦や木材から切り出したようなものです。これらの多面体の構成要素には、面、辺、頂点がありますが、その個数を勘定すると次のようになります。
| \ | 面 | 辺 | 頂点 |
| 四面体 | 4 | 6 | 4 |
| 三角柱 | 5 | 9 | 6 |
| 直方体 | 6 | 12 | 8 |
3次元なら、絵を描いたり実物を見て勘定できますが、一般のn次元における多面体の構造はなかなか想像しにくいものです。各次元ごとの構成要素の形状や個数を把握するだけでも一苦労です。先が思いやられますよね。
ところが、バタニン(Michael Batanin)が面白い図形を使うことを思いつきました。この図形は多面体なんですが、各次元ごとの構成要素の形状は一種類、個数は常に2個なのです。3次元の場合で言えば:
| \ | 面 | 辺 | 頂点 |
| 四面体 | 4 | 6 | 4 |
| 三角柱 | 5 | 9 | 6 |
| 直方体 | 6 | 12 | 8 |
| バタニンの図形 | 2 | 2 | 2 |
|---|
そんな好都合な図形があるのでしょうか?
バタニンの球体
バタニンの図形は球体(globe)と呼ばれますが、3次元なら二面体、2次元なら二辺形と呼ぶのがふさわしいでしょう。これらの図形はいずれも、1つの内部(身が詰まっている)を持ち、境界(縁<ふち>、周囲)が2つの部分に別れています。ここでは、境界の片一方を上端、もう一方を下端と呼ぶことにします*5。下の図と表を眺めてください。([追記 date="2020-02-18"]n = -1 の'*'については、この節の最後に追記をしました。[/追記])
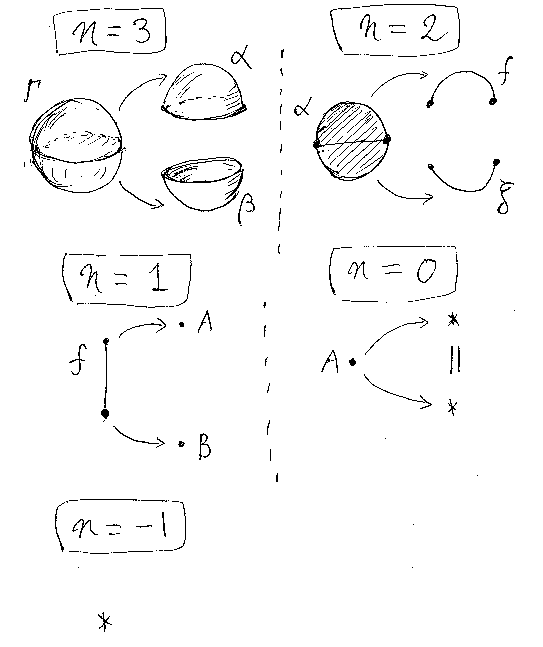
| 次元n | 球体(の記号) | 上端(の記号) | 下端(の記号) |
| 3 | Γ | α | β |
| 2 | α | f | g |
| 1 | f | A | B |
| 0 | A | * | * |
| -1 | * | なし | なし |
3次元の球体Γ<ガンマ>があると、その境界(表面)は球面です。この球面が上側のお椀と下側のお椀に別れているのです。上側をα、下側をβとします。すぐ上で定義した言葉使いだと、Γの上端がα、下端がβです。
さて、Γの上端であるαに注目しましょう。これは、お椀型ですが、ふくらみをつぶして、平らにのばしてしまえば2次元の円板です。2次元円板αもまた、上側の境界と下側の境界を持ちます。それぞれ半円で、fとgとしましょう。そう、αの上端がf、下端がgです。
今度は、αの上端であるfに注目する番です。fは半円形ですが、曲がりを取り去りまっすぐにすれば1次元の線分です。1次元線分fもまた、上側の境界と下側の境界を持ちます。それぞれは点で、AとBとします。もうお分かりですね、fの上端がA、下端がBです。
これで終わりじゃないのですよ。fの上端であるAにもさらに上端と下端があります。点Aは0次元の図形なので、その上端/下端は-1次元の図形となります。図では星印で表しました。ミステリアスに考える必要はありません。「*」と書かれた-1次元のモノがただ1つだけ存在すると考えます。-1次元のモノはただ1つなので、Aの上端も下端も必然的に*です。
[/追記]
- Title: Monoidal Globular Categories As a Natural Environment for the Theory of Weak n-Categories
- Author: M. A. Batanin
- URL: https://core.ac.uk/download/pdf/82457102.pdf
- Pages: 65p
モノイド積は、0-セルだけでなく任意次元のセルにも定義されます。例えば、2-セルには、縦結合と横結合とモノイド積の3つの演算があります。
この記事では、(-1)次元のセルに言及しているだけで、モノイド積に関する記述は省略しています。今(2020年)思うに、中途半端でしたね。修正しませんけど。
[/追記]
3-圏とはどんな世界なのか:高次ホムセット
3-圏は、3-セル、2-セル、1-セル、0-セルから構成される世界です。3, 2, 1, 0次元のセルは、どれもバタニンの球体の形をしているとしましょう。とある3-圏をTとして、Tのなかを探ってみることにします。
3-圏Tを構成する3-セルの全体をT(3)とします。同様に、T(2), T(1), T(0)は、2-セル、1-セル、0-セルの集合です。特に、T(1)とT(0)だけを見ると、通常の圏になっていて、f∈T(1)として、fの上端はdom、下端はcodで与えられます。
同じ次元の2つのセルが共端だとは、その上端と下端が一致することです。0-セルの場合、どんな0-セルAでも「Aの上端 = Aの下端 = *」だったので、どの2つの0-セルA, Bを取っても共端になります。1-セルの場合の共端は、既に定義した射の共端に一致します。共端という概念は、バタニン流のn-圏の定式化(globular approach)でとても重要なものです。シッカリと把握してください。
それでは、下の図を眺めながら、3-圏Tの構造をジックリと分析しましょう。
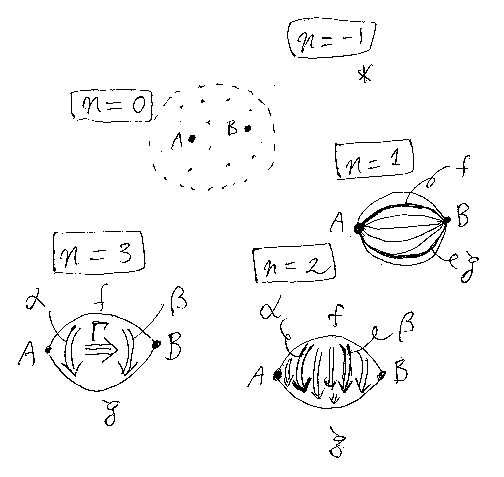
まず、-1次元のモノは*だけです。どんな0-セル(対象)でも、その上端/下端は*なので、任意の0セルA, Bは共端でした。さて、共端なA, Bに対して、A→B という1-セル(射)の全体をT(1)(A, B) と書きます。普通の圏論の言葉では、T(1)(A, B)はホムセットですね。実は、任意の0-セルは *→* という形だとみなせるので、T(0)はT(0)(*, *) という0次元ホムセットとしても書けます; T(0) = T(0)(*, *)
1次元のホムセットT(1)(A, B)には、普通たくさんの1-セルが含まれます(別に「たくさん」である必要はないが)。f, g∈T(1)(A, B)を選ぶと、今度はT(2)(f, g)が定義できます。T(2)(f, g)は、上端がf、下端がgである2-セルの集合です。このような2-セルを僕は、α::f⇒g と書き表すことにしています。fとgがA→Bであることも一緒に示せば、α::f⇒g:A→B です。
次に、T(2)(f, g)から、2つの2-セルα、βを選びます。すると、αを上端、βを下端とする3-セルの集合T(3)(α, β)が決まります。Γ∈T(3)(α, β)であるとき、Γ:::α(三本棒矢印)β と書きたいのですが、三本棒矢印を表す一文字がないので代わりの記号、≡> でも使いましょう。この記号で書けば、Γ:::α≡>β::f⇒g:A→B ってことです。
つぶれた球体と円板の関係:高次恒等
前節で、高次ホムセットの構造が明らかになりました。一般的に言えば、共端なn-セルΦとΨがあると、T(n+1)(Φ, Ψ) が定まるということです。特にn = -1 のとき T0(*, *) は対象の集合、n = 0 のとき T1(A, B) は普通のホムセットとなります。
圏の構造を定めるには、ホムセット以外に、恒等と結合(合成)が必要です。恒等とは、A∈T(0)(*, *) に対して、id(A)∈T(1)(A, A) を対応させるメカニズムです。Aは本来0次元なモノですが、idにより無理矢理1次元なモノとみなすわけです。言葉を換えて言えば、id(A)はT(1)(A, A)に入っていますが、事実上は0次元なのです(無理に1次元にしているので)。
0次元を1次元に格上げするid写像を一般化すれば、n次元を(n+1)次元に格上げするメカニズムになります。下の図を見てください。
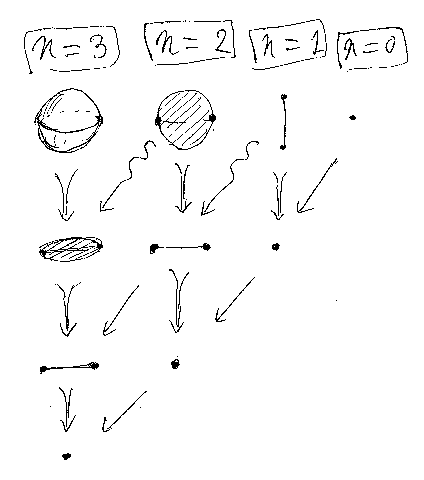
n = 3 のところを見ましょう。普通の3-セルは3次元の球体です。上端=上の半球面α と 下端=下の半球面β は異なるのが普通ですが、もちろん同一でもかまいません。上端=下端=αである球体をつぶしてしまえば、円板αと区別できなくなります。図の n = 2 の一番上は円板ですが、円板をつぶれた球体とみなすこともできます。その「みなし」が左斜め下に向かう矢印です。αが円板=2-セルのとき、id(α)は id(α):::α≡>α というつぶれた球体=3-セル となるわけです。
他の次元でも同じです、図で斜めの矢印は次元を格上げするid写像です。下に向かう矢印はつぶす操作です。id写像で格上げされた図形は、つぶれた図形だということです。
多様な隣接関係:高次結合
ホムセットと恒等の高次元版がどういうものか見当は付きました。残るは結合(合成)です。n-セルとn-セルから新しいn-セルを作り出す演算ですね。特に n = 1 のときは、普通の射の結合になるはずです。
普通の圏でも、勝手な2つの射の結合は無理です。隣接する射の対にしか結合は定義できません。n-圏でも事情は同じで、隣接するn-セルのあいだにしか結合は定義できません。となると、「n-セルが隣接しているとはどういうことか」が問題になります。
2つの2-セルα、βの場合、α::f⇒g:A→B、β::g⇒h:A→B のとき、αとβは1-セルgを境界として隣接しています。実はそれだけではなくて、γ::u⇒v:B→C があると、αとγは0-セルBを境界として隣接しているのです。つまり、「1-セルを境界とする隣接」と「0-セルを境界とする隣接」の2種類あるのです(下図参照)。隣接の形態が2種類あるので、結合も2種類あって、それを縦結合と横結合と区別しています。
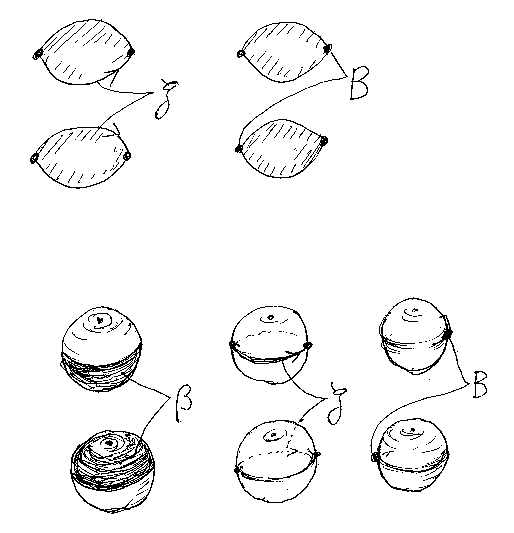
3次元の場合を考えてみましょう。容易に想像がつくように、2つの3-セル(球体)の隣接は、「2-セルを境界とする隣接」「1-セルを境界とする隣接」「0-セルを境界とする隣接」の3種類になります。そして、それぞれの隣接形態ごとに結合も3種類になります。通常の圏と同様に計算が進むためには、恒等と結合に関して単位律と結合律が成立している必要があります。
今回はこれくらいにしときます。厳密な定義は全然してませんが、n-圏の雰囲気、特に“図形達が織りなす世界”としての雰囲気は伝わったのではないでしょうか。-1次元の恒等と0次元の結合は取り上げませんでしたが、ここから別な面白い話題へと誘導されます。それはまた機会があれば。