モノイド圏の随伴性を“豊饒圏の圏”の随伴性に持ち上げる：計画編

「テンパリー／リーブ圏とカウフマンのスケイン関係式」において、「たぶん成立するだろう」みたいなことを幾つか書いています。そのひとつに次の随伴性があります。

k-LinCat(Lin_k(C), D) $\stackrel{\sim}{=}$ Cat(C, U(D))

ここで、k-LinCatはk-線形圏の圏です。Lin_k(-)は単なる圏からk-線形圏を作る関手で、集合の線形化（自由ベクトル空間を作る操作）をホムセットごとに適用して、圏全体を線形化します。Uは、すべてのホムセットのk-線形構造を忘れる忘却関手です。

この形を見ると、F:S→V, G:V→S が随伴関手対 F -| G のとき、次の随伴関手対が作れそうな気がします。（この記事の本文と記法を合わせるために、C, Dはローマン体です。）

V-Cat(F_☆(C), D) $\stackrel{\sim}{=}$ S-Cat(C, G_☆(D))

ここで、V-CatとS-Catは、豊饒圏の圏です。F_☆:S-Cat→V-Cat と G_☆:V-Cat→S-Cat は、モノイド圏のあいだの関手F, Gを、“豊饒圏の圏”のあいだの関手に持ち上げたものです。

上記の“持ち上げられた随伴性”はいかにも成立しそうです。が、実際に確認しようとしたらヤッパリめんどくさい。とりあえず、“持ち上げられた随伴性”を示す手順について考えてみます。

内容：

言葉と記号の約束
素朴なアイデア
超巨大な圏
様々な圏を整理する
手順（予定）

言葉と記号の約束

後で使う言葉と記法について以下にダラダラと書き連ねます。

S, Vなどのイタリックの文字はモノイド圏を表すとします。モノイド圏のあいだの関手としてはモノイド関手を想定します。ただし、モノイド関手には幾つかの種類があります。

厳密モノイド関手（strict monoidal functor）
タイト・モノイド関手（tight monoidal functor, 強モノイド関手（strong monoidal functor）と呼ぶことが多い）
ラックス・モノイド関手（lax monoidal functor）
反ラックス・モノイド関手（oplax monoidal functor, ラックス・余モノイド関手（lax comonoidal functor）とも呼ぶ）

最近僕は、強モノイド関手の代わりにタイト・モノイド関手と呼んでいます。形容詞「強」は他で使われるので重複や混乱を避けたいからです。モノイド圏と各種のモノイド関手については、次の記事を参照してください。

Sがモノイド圏のとき、S = (S, ×, I, α, λ, ρ) でSのモノイド圏構造を表すとします。各種の律子α, λ, ρは特に必要なければ省略し、S = (S, ×, I) とも書きます。

Xは集合として、C:X×X→|S|, γ:X×X×X→Mor(S), ι:X→Mor(S) の四組を C = (X, C, γ, ι) のように書くことにして、Cが特定の条件を満たすときS-豊饒圏（S-enriched category）と呼びます。集合Xを|C|と書けば、C = (|C|, C, γ, ι)、あるいは|C|を省略して C = (C, γ, ι) とも書きます。Cが満たすべき特定の条件については、次の記事を参照してください。

S-豊饒圏を考えるとき、モノイド圏Sを豊饒化ベース圏（enriching category, base category）と呼びます。

この記事では、豊饒化ベース圏はS, Vなどのイタリック体で書きますが、豊饒圏はイタリックではなくてC, Dなどのローマン体で書くことにします。結合γ、恒等ιなどが「どの豊饒圏のものか？」を明示したいなら、γ^C, ι^Cのような上付き添字にします。下付きは、γ^C_a,b,c:C(a, b)×C(b, c)→C(a, c) のように使います。特に必要でない限りは上付き添字は省略します。

CとDがS-豊饒圏のとき、CからDへのS-豊饒関手（S-enriched functor）は f:C→D のように小文字で書きます。射と紛らわしい、って？豊饒圏では射は存在しないんですよ。Cのホム対象はSの対象ですが、Sの対象が集合とは限らないので、“ホムセットの要素”としての射は（一般には）存在しないのです。

豊饒圏のあいだの豊饒関手fは、f:|C|→|D| という集合のあいだの写像と、a, b∈|C| で添字付けされたSの射の族 f_a,b:C(a, b)→D(f(a), f(b)) in S からなります。f(a)の形のときは対象のあいだの写像、f_a,bの形に書いたときはホム対象（Sの対象）のあいだの射の意味とします。豊饒関手が満たすべき条件はいずれ述べる機会があるでしょう（今は割愛します）。

S-豊饒圏を対象としてS-豊饒関手を射とする圏をS-Catと書きます。S-Catは、モノイド圏Sを豊饒化ベース圏とする豊饒圏の圏です。一部、定義を省略（先延ばし）したところもありますが、以上で、圏としてのS-Catは定義できました。

自然変換のS-豊饒版もあります。C, DがS-豊饒圏、f, g:C→D がS-豊饒関手のとき、S-豊饒自然変換（S-enriched natural transformation） j::f⇒g:C→D を定義できます。S-豊饒自然変換まで考えると、S-Catは単なる圏ではなくて2-圏となります。S-Catを圏と考えるか、それとも2-圏と考えるかは場合・状況によりけりです。

素朴なアイデア

我々が示したいことは、F:S→V, G:V→S がモノイド圏のあいだの随伴関手対のとき、FとGを豊饒圏の圏V-Cat, S-Catまで持ち上げた関手 F_☆:S-Cat→V-Cat, G_☆:V-Cat→S-Cat が再び随伴関手対になることです。

特別なケースとして、S = Set, V = Vect_kで、Fは自由ベクトル空間を生成する関手、Gはベクトル空間にその台集合を対応させる忘却関手とします。このとき、F -| G （FとGは随伴関手対）なので、上記の命題が成立すれば、F_☆ -| G_☆ となります。F_☆:Set-Cat→Vect_k-Cat は普通の圏からk-線形圏を作る関手、G_☆:Vect_k-Cat→Set-Cat はk-線形圏の線形構造を忘れて単なる圏とみなす関手です。

Set-Catは普通の（小さい）圏の圏なのでCatと同じです。また、Vect_k-Catはk-LinCat（k-線形圏の圏）と書いて、F_☆ = Lin_k, G_☆ = U と置き換えれば、随伴性は次の形でも書けます。

k-LinCat(Lin_k(C), D) $\stackrel{\sim}{=}$ Cat(C, U(D))

これは、「テンパリー／リーブ圏とカウフマンのスケイン関係式」で仮定した命題そのものです。

さて、上記の“随伴性の持ち上げ”はどうやったら示せるでしょうか？随伴性をニョロニョロスタイルで書いてみましょう。関手の図式順結合と自然変換の横結合は*で書くことにして、ε::Id_S→F*G:S→S を随伴の単位、η::G*F⇒Id_V:V→V を随伴の余単位とします。([追記]ウギャッ、ε, ηの使い方が普通の習慣と逆でした。ηが単位、εが余単位のときが多いです。めんどうだから直さないけど。[/追記])このとき、ニョロニョロ関係式（snake relation）は次の2つの等式となります。（「;」は自然変換の図式順縦結合です。）

(ε*F);(F*η) = F
(G*ε);(η*G) = G

これはニョロニョロ図で表現できますが、図は後で挙げます。

もし、F_☆, G_☆以外に ε☆::Id_S-Cat→F_☆*G_☆:S-Cat→S-Cat と η_☆::G_☆*F_☆⇒Id_V-Cat:V-Cat→V-Cat がうまく定義できて、しかも縦結合「;」と横結合「*」が(-)☆で保存されるなら、次の等式が成立するはずです。

(ε_☆*F_☆);(F_☆*η_☆) = F_☆
(G_☆*ε_☆);(η_☆*G_☆) = G_☆

つまり、 S-Cat, V-Cat, F_☆, G_☆, ε_☆, η_☆ が随伴性を定義することになります。これは求める結果に他なりません。

となると、対応 (-) |→ (-)_☆ を構成して、それが縦結合／横結合を保存することを示せば随伴性の持ち上げは出来るわけです。

超巨大な圏

前節の素朴なアイデアが正しいなら、あとは計算問題となります。手間はかかっても、順番に定義と計算をこなしていけばいいでしょう。しかし、圏のサイズの問題があります。それを説明するため、以下に、F -| G を表すストリング図の一部を示します。

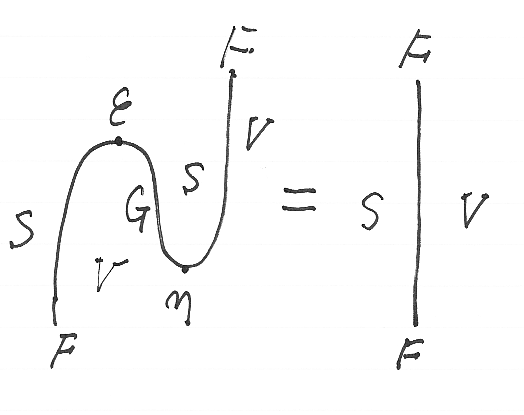
このストリング図は“どこに”に描かれているのでしょう？図に現れるS, V, F, G, ε, ηなどがどこに所属するのか？と聞いても同じです。答は「モノイド圏の圏」ですが、自然変換も登場するので、「モノイド圏を対象とする2次元の圏」と言うほうが正確です -- 随伴性は2次元の圏で定義されるべきものです。

「モノイド圏を対象とする2次元の圏」には、モノイド圏としてのSetやVect_kも入ります。「モノイド圏を対象とする2次元の圏」は大きな圏も対象に含むことになるのです。このような超巨大な圏をとても大きな圏（very large category）と呼ぶことにします。ここで考えるとても大きな「モノイド圏を対象とする2次元の圏」をMonCATと書くことにします。MonCATの射としてどのようなモノイド関手を取るか？という問題はありますが、今は気にしないことにします（いずれ決める）。

さて、(-)_☆がうまく定義できたとすれば、(-)_☆で移された先でニョロニョロ関係式が成立します。その一部をストリング図で表すなら次です。

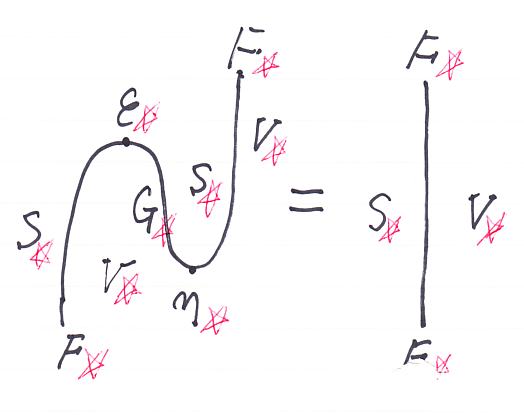
すべてに☆が付いた形です。ここで、S_☆とはS-Catのことで、V_☆はV-Catです。

この☆付きのストリング図は“どこに”に描かれているのでしょう？この図は、Set-Cat = Cat や Vect_k-Cat = k-LinCat を対象として含む圏のなかの図のはずです。つまり、とても大きな「豊饒圏の圏の圏」のなかに描かれているのです。☆付きストリング図を描く場所となる「豊饒圏の圏の圏」をEnrCatCATと記すことにします。

EnrCatCATは超巨大で正体不明です。そもそも、EnrCatCATなんて存在するのでしょうか？こんなものを考えることが許されるのでしょうか？ちょっと不安ではありますが、存在しない／考えちゃダメと言われると話が先に進まないので、とりあえず「それは在る」と思うことにします。

EnrCatCATの対象は、「豊饒圏の圏」なので2次元の圏です（豊饒自然変換が2次元の射）。2次元の圏を対象に持つ圏は3次元の構造を持つことが出来ます。つまり、EnrCatCATは3次元の圏です。ただし、今回は2次元の射まであれば十分なので、EnrCatCATの2次元部分まで考えれば間に合いそうです。

随伴性を持ち上げるための対応 (-) |→ (-)_☆ は、“とても大きな2次元の圏MonCAT”から“とても大きな2次元の圏EnrCatCAT”への2次元構造を保つ対応となります。この対応(-)_☆をEnrCatとも書くことにします。EnrCat:MonCAT→EnrCatCAT, EnrCat(-) = (-)_☆ です。

様々な圏を整理する

このテの問題を扱う際の困難は「ややこしい」ことです。使用する用語と記法に注意しないと、すぐさま混乱して何がなんだか分からなくなります。

とりあえず議論に登場する圏を列挙しておきます（下の表）。モノイド圏の次元を(1+α)としているのは、2次元の圏の極めて特殊なケース（対象が1つ）とみなせるからです。

圏（の記号）	種別	次元	大きさ	ホムセットの大きさ	親の圏
Set	モノイド圏	1+α	大きい	小さい	MonCAT
Vect_k	モノイド圏	1+α	大きい	小さい	MonCAT
S, V	モノイド圏	1+α	大きい	小さい	MonCAT
MonCAT	厳密2-圏	2	とても大きい	大きい	-
Cat	厳密2-圏	2	大きい	小さい	EnrCatCAT
k-LinCat	厳密2-圏	2	大きい	小さい	EnrCatCAT
C, D	豊饒圏	1	小さい	-	S-Cat
S-Cat	厳密2-圏	2	大きい	小さい	EnrCatCAT
EnrCatCAT	厳密3-圏	3	とても大きい	大きい	-

太字は圏の固有名詞で、太字以外は変数です。Set, Vect_kは自己豊饒圏ですが、ここでは自己豊饒構造は考えないことにします。SetやVect_kは大きい圏なので、自己豊饒構造を考えても Set-Cat = Cat, Vect_k-Cat = k-LinCat には入らないのです（Cat, k-LinCatは小さい圏の圏だから）。

次にそれぞれの圏のセル（構成素）の呼び名を表にまとめておきます。

圏（の記号）	0-セル	1-セル	2-セル
Set	集合	写像	-
Vect_k	ベクトル空間	線形写像	-
S, V	対象	射	-
MonCAT	モノイド圏	モノイド関手	モノイド自然変換
Cat	小さい圏	関手	自然変換
k-LinCat	小さい線形圏	線形関手	線形自然変換
C, D	集合の要素	-	-
S-Cat	小さい豊饒圏	豊饒関手	豊饒自然変換
EnrCatCAT	豊饒圏の圏	2-関手	2-自然変換

それ以外のセルと結合（圏の演算）を表す記号は以下のようにします。

圏（の記号）	0-セル	1-セル	2-セル	縦結合	横結合
Set	A, B	f, g	-	;	×
Vect_k	V, W	f, g	-	;	$\otimes$
S, V	A, B,V, W	f, g	-	;	×, $\otimes$
MonCAT	S, V	F, G	α, β	;	*
Cat	C, D	F, G	α, β	;	*
k-LinCat	C, D	F, G	α, β	;	*
C, D	a, b	-	-	-	-
S-Cat	C, D	f, g	j, k	;	*
EnrCatCAT	S-Cat, V-Cat	X, Y	Φ, Ψ	;	*