パートナーエージェントという結婚情報サービスがあります: http://www.p-a.jp/ 。この会社のロゴマークは  。方向を変えてみると:
。方向を変えてみると:
 とか
とか  とか。
とか。
このマークを電車内の広告で見て僕は、「これは可換性の絵だよな、見る方向により余可換性とも取れる」と思いました。婚活と可換性/余可換性がどんな関係かは知りませんけど。
ちょっと説明しましょう。
例には自然数の集合Nだけを使います。N = {0, 1, 2, 3, ...} ですね。N上の二項演算とは、N×N→N という写像です。一般のモノイド圏(×をモノイド積とする)では、圏の対象をAとして、A×A→A という射がA上の二項演算です。
一般的な二項演算を積(product)とか乗法(multiplication)と呼ぶことも多いです。N上の二項演算の例には足し算 (n, m) |→ n + m があります。二項(ペア)の左側を取り出す演算 (n, m) |→ n も立派な二項演算です。
“二項演算=積=乗法”の圏論的な双対概念が余二項演算です。N上の余二項演算は、N→N×N という写像です。一般のモノイド圏でも定義は同じ。余二項演算を、余積、余乗法と呼ぶことが多いですね。
一番簡単なN上の余二項演算の例は、1個の自然数を2つにコピーする操作 n |→ (n, n) でしょう。n |→ (n, 0) も余二項演算の例です。
ペア (n, m) の左右を入れ替える演算をσとします。σ(n, m) = (m, n) です。なにか二項演算 b:N×N→N があったとき、bが可換であるとは次が成立することです。
- σ;b = b
引数を使って書き下すと、 (σ;b)(n, m) = b(σ(n, m)) = b(m, n) なので、次のように言っても同じです。
- b(m, n) = b(n, m)
足し算 λ(n, m).[n + m] は可換ですが、左側を取り出す λ(n, m).n は可換ではありません。
可換性と同様に、余二項演算 c:N → N×N の余可換性は次の等式で定義されます。
- c;σ = c
c(n) = (c1(n), c2(n)) と書くなら:
- (c2(n), c1(n)) = (c1(n), c2(n))
λn.[(n, n)] は余可換ですが、λn.[(n, 0)] は余可換ではありません。可換性/余可換性は、対称モノイド圏(symmetric monoidal category)なら定義できる概念です。
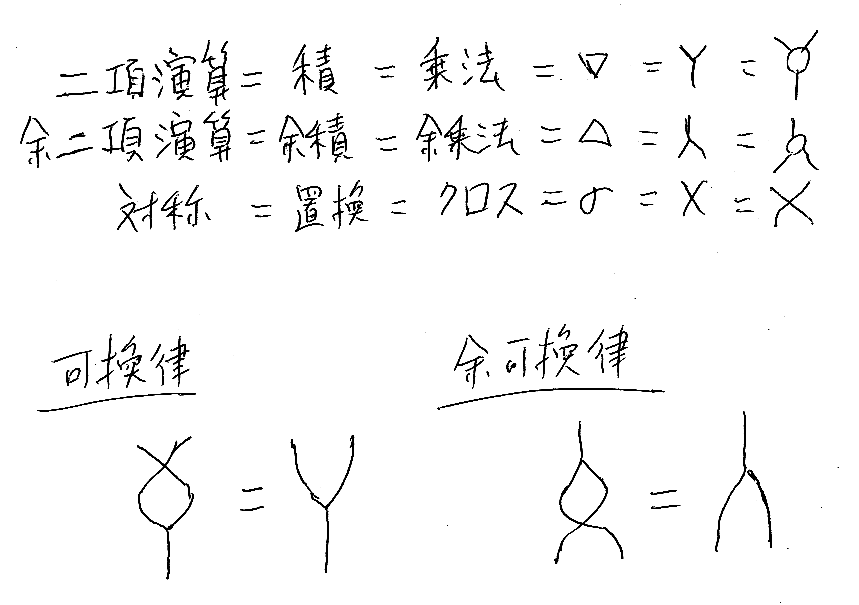
さて絵算では、二項演算(積、乗法)にYの形の絵記号、余二項演算(余積、余乗法)にYの逆の形の絵記号を使います。また、絵にあわせて∇とΔを二項演算/余二項演算を表す記号として使うことがあります。そのような記号/絵記号の例は「ホップ代数の絵算 3:対蹠が反準同型射であること」とか見てください。「双モノイドの簡単な例 -- 自然数の足し算と余足し算」にも、二項演算と余二項演算の例があります。
まとめると次の手描きチートシートになります。ここに、パートナーエージェントのロゴが出てくるんです。([追記]ん? あのロゴは、最近流行りのクロスカップリングを表すのか?[/追記])