このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

バタニン・ツリー 再論

雑記／備忘

バタニン・ツリーについては、以下の過去記事に書いています。

ディーン達の論文の p.6 "2 Batanin trees" でもバタニン・ツリーを扱っています。

  • [DFMRV22-24]
  • Title: Computads for weak ω-categories as an inductive type
  • Authors: Christopher J. Dean, Eric Finster, Ioannis Markakis, David Reutter and Jamie Vicary
  • Submitted: 18 Aug 2022 (v1), 20 Mar 2024 (v3)
  • Pages: 67p
  • URL: http://arxiv.org/abs/2208.08719

バタニン・ツリーはやっぱり重要なので、もう一度調べてみます。バタニン・ツリー特有な話の前に、ツリーとリストの一般論を入れます。最後にバタニン・ツリーに特有なポジション集合とポジションのアドレスを定義します。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\mbf}[1]{\mathbf{#1}}
%\newcommand{\mfk}[1]{\mathfrak{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{－} }
\newcommand{\In}{ \text{ in } }
%\newcommand{\On}{ \text{ on } }
\newcommand{\id}{\mathrm{id} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\T}[1]{\text{#1} }
\newcommand{\EL}{\varepsilon} % Empty List
\newcommand{\Cons}{\mathop{\blacktriangleright} }
\newcommand{\Snoc}{\mathop{\blacktriangleleft} }
\newcommand{\Apnd}{\mathop{\#} }
\newcommand{\BCons}{\mathop{\|\!\blacktriangleright} }
`$

内容：

バタニン・ツリーの参考文献

過去記事「指標の話： ペースティング図とバタニン・ツリー」と「球体集合達の圏の構文表示 1/2」 で参照したフィンスター／ミムラムの論文、p.7 "D. Batanin trees" にバタニン・ツリーについて書いてあります。

  • [FM17-]
  • Title: A Type-Theoretical Definition of Weak ω-Categories
  • Authors: Eric Finster, Samuel Mimram
  • Submitted: 9 Jun 2017
  • Pages: 12p
  • URL: https://arxiv.org/abs/1706.02866

過去記事「指標の組織化と表現方法と呼び名は色々だ」で参照したマルカキスの論文、p.27 付近にもバタニン・ツリーの記述があります。

  • [Mar23-]
  • Title: Computads for generalised signatures
  • Author: Ioannis Markakis
  • Submitted: 21 Mar 2023 (v1), 9 Jun 2023 (v2)
  • Pages: 39p
  • URL: https://arxiv.org/abs/2303.11978

バタニン・ツリーへの直接的言及はないのですが、アラウージョの論文も参考になりそうです。

  • [Ara22-]
  • Title: Simple string diagrams and n-sesquicategories
  • Author: Manuel Araújo
  • Submitted: 18 Feb 2022 (v1), 16 Nov 2022 (v4)
  • Pages: 42p
  • URL: https://arxiv.org/abs/2202.09293

そして、冒頭で参照したディーン達の論文にもバタニン・ツリーの記述があります。

バタニン・ツリーはただのツリー

バタニン・ツリーはごくごく普通のツリーです。普通のツリーが、ある特別な状況で使われるときにバタニン・ツリーと呼ばれるだけです。

普通のツリーを定義するための普通の方法は、有向グラフの特別なものをツリーと定義することです。有向グラフをもとにツリーを定義する話は以下の過去記事にあります（この記事でも説明しますが）。

兄弟ノードのあいだに順序がないツリーについては、以下の過去記事も参考になるでしょう。

ツリーを有向グラフとみなしたときの辺の方向として、root-to-leaf と leaf-to-root の二つの選択肢がありますが、ここでは root-to-leaf とします（別にどっちでもいいけど）。

有向グラフについては知っているとします。以下、「グラフ」は有向グラフのことです。グラフ $`X`$ のノードの集合と辺〈edge〉の集合を次のように書きます。

$`\quad \mrm{Node}(X)\\
\quad \mrm{Edge}(X)
`$

「頂点」と呼ばずに「ノード」と呼んでいるのは気分だけの問題です、理由はありません。

グラフ $`T`$ と特定のノード $`r\in \mrm{Node}(T)`$ の組 $`(T, r)`$ が有限ツリー〈finite tree〉であるとは：

  1. $`\mrm{Node}(T)`$ も $`\mrm{Edge}(T)`$ も有限集合である。
  2. 任意のノード $`x\in \mrm{Node}(T)`$ に対して、特定のノード $`r`$ から $`x`$ に至るパスが一本だけある。

ノード $`r\in \mrm{Node}(T)`$ をルートノード〈root node〉、または単にルート〈root〉と呼びます。ルートからルートに至るパスは空パスです。ノードがルートだけで辺がないグラフも有限ツリーです。

記号の乱用で、有限ツリーを以下のように書きます。

$`\quad T = (T, r)`$

有限ツリー $`T`$ の任意のノード $`x\in \mrm{Node}(T)`$ に対して、ルート $`r`$ から $`x`$ に至るパスの長さを $`\mrm{height}_T(x)`$ と定義します。

$`\quad \mrm{height}_T : \mrm{Node}(T) \to \mbf{N} \In \mbf{Set}`$

$`\mrm{height}_T`$ を $`T`$ の高さ関数〈height function〉と呼びます。高さ関数を深さ関数とかレベル関数と呼ぶこともあります。どう呼ぶかは趣味の問題です。

有限ツリー $`T`$ の $`\mrm{Node}(T)`$ は有限集合なので、高さ関数の像集合も有限集合になります。

$`\quad \mrm{Img}(\mrm{height}_T) \subseteq \mbf{N}`$
$`\quad \mrm{Img}(\mrm{height}_T) \in |\mbf{FinSet}|`$

有限集合 $`\mrm{Img}(\mrm{height}_T)`$ の最大値を、有限ツリー $`T`$ の高さ〈height〉と定義します。

$`\quad \mrm{Height}(T) := \mrm{max}( \mrm{Img}(\mrm{height}_T) )`$

$`T`$ の高さ関数 $`\mrm{height}_T`$ と、$`T`$ の高さ $`\mrm{Height}(T)`$ は別物なので混同しないように注意してください。

有限ツリー $`T`$ の任意のノード $`x\in \mrm{Node}(T)`$ に対して、その子ノード〈child node〉の集合 $`\mrm{Child}_T(x)`$ は以下のように定義します。

$`\quad \mrm{Child}_T(x) := \{ y\in \mrm{Node}(T) \mid
\exists e\in \mrm{Edge}(T).\, \mrm{src}(e) = x \land \mrm{trg}(e) = y \}
`$

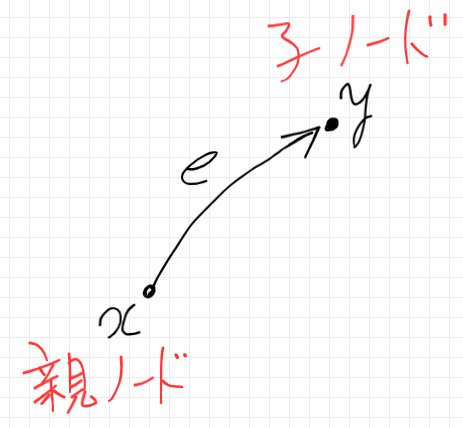
子ノードの集合を対応させる関数は、次のような関数になります。$`\mrm{Pow}(\hyp)`$ はベキ集合です。

$`\quad \mrm{Child}_T : \mrm{Node}(T) \to \mrm{Pow}(\mrm{Node}(T)) \In \mrm{Set}`$

もし $`\mrm{Child}_T(x) = \emptyset`$ ならば、$`x`$ はリーフノード〈leaf node〉、または単にリーフ〈leaf〉と呼びます。

任意のノード $`x\in \mrm{Node}(T)`$ に対する子ノードの集合 $`\mrm{Child}_T(x)`$ に全順序〈total order〉が入っている有限ツリーは、順序付き有限ツリー〈ordered finite tree〉と呼びます。

以下、有限ツリーしか扱わないので、有限ツリーを単にツリー〈tree〉、順序付き有限ツリーを単に順序付きツリー〈ordered tree〉と呼びます。

バタニン・ツリー〈Batanin tree〉は順序付きツリー（つまり、順序付き有限ツリー）のことです。先に述べたように、特別な用途で使うことを想定してバタニン・ツリーと呼ぶだけで、それ自体は何の変哲もない“いわゆるツリー”です。

習慣として、バタニン・ツリーは平面内に、ルートが下端で上に枝が伸びるレイアウトで描きます。次は、XyJax（このブログの図式描画に使っているツール）で描いたバタニン・ツリーの一例です（「指標の話： ペースティング図とバタニン・ツリー」より再掲）。

$`\quad \xymatrix{
{\bullet} \ar@{-}[dr]
\ar@{.}[rrrrr]
&{}
&{\bullet} \ar@{-}[dl]
&{}
&{\bullet} \ar@{-}[d]
&{2}
\\
{}
\ar@{.}[rrrrr]
&{\bullet} \ar@{-}[drr]
&{}
&{\bullet}\ar@{-}[d]
&{\bullet}\ar@{-}[dl]
&{1}
\\
{}
\ar@{.}[rrrrr]
&{}
&{}
&{\bullet}
&{}
&{0}
}`$

横方向の点線は、ノードの高さを示すための補助線で、ツリーの一部ではありません。辺〈エッジ〉の向きは描いてませんが、下から上〈root-to-leaf〉です（約束を決めておけば、どちらでもいいが）。

リストとリスト処理

集合 $`X`$ の要素を成分〈項目〉とするリストの集合を $`\mrm{List}(X)`$ と書きます。略記としてクリネスター〈Kleene star〉も使います。

$`\quad X^* := \mrm{List}(X)`$

空リストは $`\varepsilon`$ で表します。

Lispの伝統に従い、リストの先頭に成分を追加する演算〈関数 | 写像〉を $`\mrm{cons}`$〈コンス〉と書きます。

$`\quad \mrm{cons}_X : X \times\mrm{List}(X) \to \mrm{List}(X) \In \mbf{Set}`$

リストの末尾に成分を追加する演算は $`\mrm{snoc}`$〈スノック〉と書きます。

$`\quad \mrm{snoc}_X : \mrm{List}(X)\times X \to \mrm{List}(X) \In \mbf{Set}`$

"cons" は "construct" から、"snoc" は "cons" の綴りを逆にしたものです。

リストの連接（並べてつなぐ）演算は、Lispでは $`\mrm{append}`$ と呼びます。

$`\quad \mrm{append}_X : \mrm{List}(X)\times \mrm{List}(X) \to \mrm{List}(X) \In \mbf{Set}`$

次の中置演算子記号を使うことにします。

  • $`\mrm{cons}`$〈コンス〉の中置演算子記号は $`\Cons`$
  • $`\mrm{snoc}`$〈スノック〉の中置演算子記号は $`\Snoc`$
  • $`\mrm{append}`$〈アペンド〉の中置演算子記号は $`\Apnd`$

$`\quad (\Cons) : X \times\mrm{List}(X) \to \mrm{List}(X) \In \mbf{Set}`$
$`\quad (\Snoc) : \mrm{List}(X)\times X \to \mrm{List}(X) \In \mbf{Set}`$
$`\quad (\Apnd) : \mrm{List}(X)\times \mrm{List}(X) \to \mrm{List}(X) \In \mbf{Set}`$

集合 $`X`$ によらずに同じ演算子記号を使うので、オーバーロードされた総称〈ジェネリック〉な演算子です。

リストの特徴は、それが帰納的〈inductive〉に定義できることです。例えば、次のように定義できます。

  1. 空リスト $`\EL = ()`$ はリストである。
  2. $`l`$ がリスト、$`x\in X`$ なら、$`x\Cons l`$ はリストである。
  3. 以上で得られるものだけがリストである。

$`\mrm{List}(X)`$ が帰納的に定義されるので、$`\mrm{List}(X)`$ 上の関数を、帰納的構成に沿って定義できます。こうして定義された関数は「再帰的関数」と呼ぶことが多いようです（「帰納」と「再帰」の使い方は「再帰的構成のために： 順序数の圏 // 再帰と帰納」参照）。

バタニン・ツリーとリスト

リストは帰納的に定義できましたが、バタニン・ツリー（ただのツリー）も帰納的定義を持ちます。バタニン・ツリーの定義のために、リストの定義も一緒に使います。

ツリーのノードを表す“象形文字”として '$`\bullet`$' を使います。$`\EL`$ は空リスト $`()`$ でした。

  1. 空リスト $`\EL = ()`$ はバタニン・ツリーのリストである。
  2. $`L`$ がバタニン・ツリーのリスト、$`B`$ がバタニン・ツリーなら、$`B\Cons L`$ はバタニン・ツリーのリストである。
  3. 以上で得られるものだけがバタニン・ツリーのリストである。
  4. $`L`$ がバタニン・ツリーのリストなら、$`\bullet L`$ はバタニン・ツリーである。特に、$`\bullet \EL = \bullet ()`$ はバタニン・ツリーである。
  5. 以上で得られるものだけがバタニン・ツリーである。

要するに、既にバタニン・ツリーのリストがあれば、それにルートを表す '$`\bullet`$' を前置すると、それもまたバタニン・ツリーになる、ということです。このルールに基づいてバタニン・ツリーの例を幾つか挙げると：

  1. $`\bullet()`$
  2. $`\bullet(\bullet())`$
  3. $`\bullet( \bullet(), \bullet() )`$
  4. $`\bullet( \bullet( \bullet(), \bullet() ))`$
  5. $`\bullet( \bullet( \bullet(), \bullet() ), \bullet() )`$
  6. $`\bullet( \bullet( \bullet(), \bullet() ), \bullet(), \bullet(\bullet()) )`$

最後の例は、先に挙げた図（再掲）のバタニン・ツリーです。

$`\quad \xymatrix{
{\bullet} \ar@{-}[dr]
\ar@{.}[rrrrr]
&{}
&{\bullet} \ar@{-}[dl]
&{}
&{\bullet} \ar@{-}[d]
&{2}
\\
{}
\ar@{.}[rrrrr]
&{\bullet} \ar@{-}[drr]
&{}
&{\bullet}\ar@{-}[d]
&{\bullet}\ar@{-}[dl]
&{1}
\\
{}
\ar@{.}[rrrrr]
&{}
&{}
&{\bullet}
&{}
&{0}
}`$

$`\bullet()`$ を単に $`\bullet`$ と略記すると視認性が向上します。この略記は色々な場面でよく使われています。

  1. $`\bullet`$
  2. $`\bullet(\bullet)`$
  3. $`\bullet( \bullet, \bullet )`$
  4. $`\bullet( \bullet( \bullet, \bullet ))`$
  5. $`\bullet( \bullet( \bullet, \bullet ), \bullet )`$
  6. $`\bullet( \bullet( \bullet, \bullet ), \bullet, \bullet(\bullet) )`$

バタニン・ツリーの帰納的定義に基づいて、バタニン・ツリーの高さ（ノードの高さではない！）を定義してみましょう。

  1. $`\mrm{Height}(\bullet () ) := 0`$
  2. バタニン・ツリーのリストを $`L = (B_1, \cdots ,B_n)`$ として、
    $`\mrm{Height}(\bullet L) := 1 + \mrm{max}_{i = 1, \cdots, n}\, \mrm{Height}(B_i)`$

さて、すべてのバタニン・ツリーからなる集合を $`\mrm{BaTree}`$ とします。次のような関数を定義します。

  1. バタニン・ツリーのリスト $`L`$ にルートノードを追加して、バタニン・ツリー $`\bullet L`$ を作る関数 $`\mrm{br}`$
  2. バタニン・ツリー $`\bullet L`$ からルートノードを取り除いて、$`L`$ を作る関数 $`\mrm{hedge}`$

'$`\mrm{br}`$' は、バタニン・ツリー関連ではよく使われる名前ですが、僕は語源を知りません。Batanin の b と root の r かな？ '$`\mrm{hedge}`$' は、ツリーのリストは生垣〈hedge〉と呼ぶからです。これらの関数は互いに逆になります。

$`\quad \mrm{br} : \mrm{List}(\mrm{BaTree}) \to \mrm{BaTree} \In \mbf{Set}`$
$`\quad \mrm{hedge} : \mrm{BaTree} \to \mrm{List}(\mrm{BaTree}) \In \mbf{Set}`$
$`\quad \mrm{br} ; \mrm{hedge} = \id_{\mrm{List}(\mrm{BaTree})}`$
$`\quad \mrm{hedge}; \mrm{br} = \id_{\mrm{BaTree}}`$

バタニン・ツリーの用途

何度か言っているように、バタニン・ツリーそれ自体は単なる順序付き有限ツリーです。特定の用途で使われるときに「バタニン・ツリー」と呼ぶわけです。その用途とは、ペースティング図の表現です。

ペースティング図〈pasting diagram〉とは、1-圏のドット＆アロー図の高次圏への一般化です。高次圏の高次射達の組み合わせ方を、図として表したものがペースティング図です。ペースティング図は、実際に描いて使っているものですが、厳密に定義しようとすると非常に難しい。

一般的なペースティング図を厳密に定義するのは難しいのですが、そのなかでも単純で取り扱いやすいものだけに限定すると、ラベル付きの順序付き有限ツリーで表現可能〈エンコード可能〉なことが分かっています。バタニン・ツリーの用途は、単純なペースティング図の表現〈コード〉です。

バタニン・ツリーへのラベリングは特殊です。通常のラベリングは、ツリーのノードや辺〈エッジ〉にラベルを割り当てるのですが、バタニン・ツリーのラベリングでは、ツリーを平面に描いたときにできるパイ形（扇形）領域〈エリア | セクター〉にラベルを割り当てます。このことについては、次の過去記事を参照してください。

冒頭に挙げたディーン達の論文では、独特なラベリングをうまく記述するために、バタニン・ツリーに対して、もうひとつの帰納的定義を与えています。それを次節で述べます。

バタニン・ツリーの、もうひとつの帰納的定義

ディーン達は、バタニン・ツリーの集合に新しい二項演算を導入しました。リストのコンス〈cons〉演算と似てますが、引数〈被演算子〉は2つともバタニン・ツリーです。ここでは、この二項演算をバタニン・コンス〈Batanin cons〉と呼び次のように書きます。

$`\quad \mrm{baCons}: \mrm{BaTree}\times \mrm{BaTree} \to \mrm{BaTree} \In \mbf{Set}`$

バタニン・コンス $`\mrm{baCons}`$ の中置演算子記号を $`\BCons`$ とします。バタニン・コンスの定義は：

  1. $`B \BCons \bullet() := \bullet( B )`$
  2. バタニン・ツリーのリストを $`L = (B_1, \cdots ,B_n)`$ として、
    $`B \BCons \bullet L := \bullet (B \Cons L) = \bullet (B, B_1, \cdots, B_n)`$

バタニン・コンスの雰囲気的な絵を描くと次のようです。

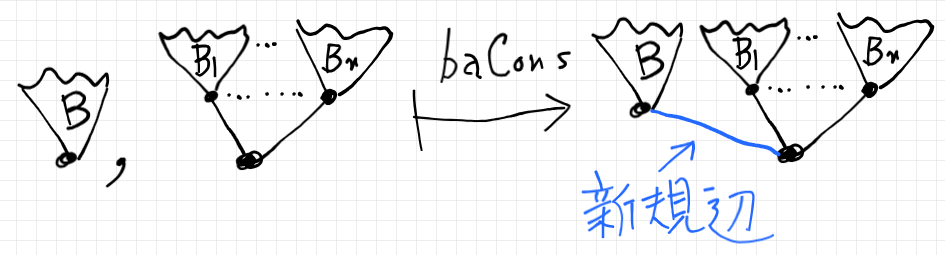
バタニン・コンスの第一引数のツリーは、第二引数のツリーの“左端”に繋がれます。このとき、新しい辺が一本増えます。

バタニン・コンスを使って、バタニン・ツリーの帰納的定義ができます。

  1. ルートだけのツリー $`\bullet ()`$ はバタニン・ツリーである。
  2. $`B, B'`$ がバタニン・ツリーのとき、$`B\BCons B'`$ もバタニン・ツリーである。
  3. 以上で得られるものだけがバタニン・ツリーである。

この帰納的定義が、最初の定義と同じ集合を生成することは証明を要しますが、構成法を丁寧に見れば、同じ集合を生成していることが分かるでしょう。

新しい帰納的定義に基づいて、バタニン・ツリーの高さを定義してみます。

  1. $`\mrm{Height}(\bullet () ) := 0`$
  2. $`\mrm{Height}(B\BCons B') := \mrm{max}( \mrm{Height}(B) + 1, \mrm{Height}( B'))`$

バタニン・ツリーのポジション集合

バタニン・ツリーのラベリングは、パイ形領域に対してラベルを割り当てるのでした（「指標の話： ペースティング図とバタニン・ツリー // バタニン・ツリーのラベリング」参照）。ラベルを割り当てる場所（パイ形領域）をポジション〈position〉とも呼びます。バタニン・ツリー $`B`$ のポジションの集合を $`\mrm{Pos}(B)`$ とします。

値を集合 $`X`$ に取るラベリング $`l`$ は、次のような写像です。

$`\quad l : \mrm{Pos}(B) \to X \In \mbf{Set}`$

バタニン・ツリー $`B`$ に対する $`\mrm{Pos}(B)`$ がちゃんと定義されてないと、ラベリングの概念もハッキリしません。$`\mrm{Pos}(B)`$ をちゃんと定義しましょう。

おおよそのアイディアは、前節の帰納的定義に沿って、$`\mrm{Pos}(B)`$ が次のようになるように定義します。

  1. $`\mrm{Pos}(\bullet ()) \cong \mbf{1}`$ （$`\mbf{1}`$ は特定された単元集合）
  2. $`\mrm{Pos}(B \BCons B') \cong \mbf{1} + \mrm{Pos}(B) + \mrm{Pos}(B')`$ （$`+`$ は集合の直和）

上記の定義をより具体的にするために、$`\mrm{Pos}(\bullet ())`$ の要素にアドレスを振ります。アドレスは二進数（自然数の二進表示）で十分ですが、もう少し扱いやすいアドレス形式を考えます。次節で述べます。

バタニン・アドレス

バタニン・ツリーのポジションに割り当てるアドレスをバタニン・アドレス〈Batanin address〉と呼ぶことにします。バタニン・アドレスは、3つの文字 'i’, 'u', 'r' から作られる文字列です。例えば、"iurru" はバタニン・アドレスです。実際には、2文字 'u', 'r' で十分ですが、視認性や分かりやすさから 'i' も入れてます。それぞれの文字の由来は次のようです。

  • 'i' は initial の意味
  • 'u' は up の意味
  • 'r' は right の意味

文字列としてのバタニン・アドレスの最初の文字は必ず 'i' です。その後には、任意個（0個でもいい）の 'u' または 'r' が並びます。

バタニン・ツリーのポジション（パイ形領域）へのバタニン・アドレスの割り当て方は、帰納的定義に基づいて定義します。

  1. ルートだけのツリーに対する $`\mrm{Pos} (\bullet ())`$ は単元集合なので、その唯一のポジションにアドレス $`\T{i}`$ を割り当てる。
  2. $`B, B'`$ がバタニン・ツリーのとき、$`B\BCons B'`$ で追加された新規辺の左の領域にアドレス $`\T{i}`$ を割り当てる。$`B`$ のポジションの各アドレスに文字 $`\T{u}`$ を左に追加した〈スノックした〉アドレスを新しいアドレスにする。$`B`$ のポジションの各アドレスに文字 $`\T{r}`$ を左に追加した〈スノックした〉アドレスを新しいアドレスにする。

次は、バタニン・ツリーのポジションにアドレスを割り振った例です。

$`\quad \xymatrix{
{\T{iuu}\,\bullet} \ar@{-}[dr]_{\T{iu}}^{\T{iru}}
\ar@{.}[rrrrr]
&{}
&{\T{iruu} \, \bullet} \ar@{-}[dl]^{\T{irru} }
&{}
&{\T{iurru} \, \bullet} \ar@{-}[d]_{\T{iurr}}^{\T{iurrr}}
&{2}
\\
{}
\ar@{.}[rrrrr]
&{\bullet} \ar@{-}[drr]_{\T{i}}^{\T{ir}}
&{}
&{\T{irru}\, \bullet }\ar@{-}[d]^{\T{irr}}
&{\bullet}\ar@{-}[dl]^{\T{irrr}}
&{1}
\\
{}
\ar@{.}[rrrrr]
&{}
&{}
&{\bullet}
&{}
&{0}
}`$

最初の文字 $`\T{i}`$ は取り除いても影響はありません。長さ 1 の文字列 $`\T{i}`$ の代わりに空列（長さ 0 の文字列）$`\EL`$ を使います。

バタニン・ツリー $`B`$ におけるバタニン・アドレスの割り当て関数を $`\mrm{baAddr}`$ とすると、次のような関数です。

$`\quad \mrm{BaAddr}_B : \mrm{BaTree} \to \{\T{u}, \T{r}\}^* \cup \{\EL \}`$

どんなバタニン・ツリー $`B`$ に対しても、$`\mrm{baAddr}_B`$ は単射になります。したがって、次のような集合の同型があります。

$`\quad \mrm{Pos}(B) \cong \mrm{Img}(\mrm{baAddr}_B)`$

しばしば、$`\mrm{Pos}(B)`$ と $`\mrm{Img}(\mrm{baAddr}_B)`$ は同一視されます。例えば、$`\mrm{Pos}(B)`$ 上の関数を定義する代わりに、$`\mrm{Img}(\mrm{baAddr}_B)`$ 上の関数を定義して済ませます。

一例として、バタニン・ツリーのポジションに対する次元関数 $`\mrm{dim}`$ を、バタニン・アドレスに対する関数として定義してみます。

  • $`\mrm{dim}(\EL) = 0`$
  • $`\mrm{dim}(\xi \Snoc \T{u}) = \mrm{dim}(\xi) + 1`$
  • $`\mrm{dim}(\xi \Snoc \T{r}) = \mrm{dim}(\xi)`$

アドレスに対して定義された $`\mrm{dim}`$ を、$`\mrm{Pos}(B)`$ 上の関数とも解釈します。

バタニン・ツリーのラベリングは、バタニン・アドレス全体の部分集合で定義された関数とみなせます。

おわりに

バタニン・ツリーに対する2種類の帰納的定義と、バタニン・ツリーのポジションの定義を納得すれば、ポジションの集合が球体集合〈globular set〉になることや、ラベリングが球体集合のあいだの射とみなせること、そしてバタニン・ツリーとペースティング図の関係なども理解できるでしょう。