「論理や型理論の圏論的意味論」より:
今年いっぱいくらい、まとまった時間が取りにくい状況があるので、長いブログエントリーは書けそうにない。短いエントリーをチョコチョコと書くことにします。短くて完結した書き物は難しいので、続き物になる可能性が高いです。
と書きましたが、その後まーまーの長さの記事を書いてます。今回もまーまーの長さの記事ですが、備忘と予定のメモです。いずれ説明するつもりの話題に関するメモです。$`
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\mbf}[1]{ \mathbf{#1} }
\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\o}[1]{ \overline{#1} }
%\newcommand{\id}{ \mathrm{id} }
\newcommand{\In}{ \text{ in }}
\newcommand{\op}{ \mathrm{op}}
`$
内容:
オプティックの圏のホムセット
最近、エンド/コエンドに関して再論(蒸し返し)をしました。
コエンドの応用として思いつくのは、オプティックの圏の定義です。オプティック(特に具象オプティック)については以下の過去記事で述べています。
上記過去記事ではコエンドを明示的には使っていませんが、具象オプティックの圏 $`\mbf{ConcOptic}`$ のホムセットをコエンドを使って書くと次のようです*1。
$`\quad {\displaystyle
\int^{R\in |\mbf{Set}|} \mbf{Set}(A, R\times B) \times\mbf{Set}(R\times Y, X)
}
`$
集合圏の代わりに、対称モノイド圏 $`\cat{C}`$ を使うと、以下のようです。
$`\quad {\displaystyle
\int^{R\in |\cat{C}|} \cat{C}(A, R\otimes B) \times\cat{C}(R\otimes Y, X)
}
`$
上記のコエンドは、パラメータ $`A,B, X,Y`$ を含むので、 $`|\cat{C}|\times |\cat{C}|`$ の要素のペア(ペアのペア)ごとに集合を対応させます。
$`\quad (|\cat{C}|\times |\cat{C}|)^2 \ni ( (A, B), (X, Y)) \mapsto \\
\quad {\displaystyle \left(\int^{R\in |\cat{C}|} \cat{C}(A, R\otimes B) \times \cat{C}(R\otimes Y, X)\right) \in |\mbf{Set}| }
`$
$`(|\cat{C}|\times |\cat{C}|)^2 \to |\mbf{Set}|`$ という対応〈集合族 | ファミリー〉があるので、集合 $`|\cat{C}|\times |\cat{C}|`$ を頂点集合とする有向グラフが定義できます。有向グラフは圏の下部構造なので、圏を定義する第一歩となります。
米田テンソル
次の定義を考えます。
$`\quad P(A, B, X, Y, R, S) :=
\cat{C}(A, R\otimes X)\times \cat{C}(S\otimes Y, B)
`$
$`P(A, B, X, Y, R, S)`$ は6つの変数〈パラメータ〉を持つ集合です。とりあえず、非常に雑な定義として、幾つかの変数により決まる集合を米田テンソル〈Yoneda tensor〉と呼ぶ、と約束します。
もう少し補足が必要です; 幾つかの変数は圏の対象または射を表します。大文字が対象で小文字が射を表すと約束すると、射に対しては集合間の写像〈関数〉が対応します。
$`\quad P(a, b, x, y, r, s) : P(A, B, X, Y, R, S) \to P(A', B', X', Y', R', S')\In \mbf{Set}\\
\text{Where}\\
\quad a : A' \to A \In \cat{C}\\
\quad b : B \to B' \In \cat{C}\\
\quad x : X \to X' \In \cat{C}\\
\quad y : Y' \to Y \In \cat{C}\\
\quad r : R \to R' \In \cat{C}\\
\quad s : S' \to S \In \cat{C}
`$
方向を図示すると:
$`\quad \xymatrix@C-1.5pc{
A
& B \ar[d]|{b}
& X \ar[d]|{x}
& Y
& R \ar[d]|{r}
& S
\\
A' \ar[u]|{a}
& B'
& X'
& Y' \ar[u]|{y}
& R'
& S' \ar[u]|{s}
}`$
そして、$`P`$ は関手性を持つとします。結局、この米田テンソル $`P`$ は、集合圏に値を持つ6引数〈6変数 | 6項〉の関手です。6つの引数には、共変と反変が混じっています。反変を反対圏を使って表すことにすると、$`P`$ のプロファイルは次のように書けます。
$`\quad P :
\cat{C}^\op \times
\cat{C} \times
\cat{C} \times
\cat{C}^\op \times
\cat{C} \times
\cat{C}^\op \to \mbf{Set} \In \mbf{CAT}
`$
「圏論のエンドとコエンドは双対なんだよ」で説明したオーバーライン記法を使うと、次のように書けます。([追記]説明不足だったので、すぐ後に補足説明を追加。[/追記])
$`\quad P(\o{a}, b, x, \o{y}, r, \o{s}) : P(\o{A}, B, X, \o{Y}, R, \o{S}) \to P(\o{A'}, B', X', \o{Y'}, R', \o{S'})\In \mbf{Set}
`$
「ラテン文字小文字は射を表す」はいいのですが、小文字 $`a`$ の最初の出現では、
$`\quad a : A' \to A \In \cat{C}`$
方向の図示では、$`a`$ を下から上の“逆行”で描いています。そして、オーバーライン記法では、
$`\quad \o{a} : A \to A' \In \cat{C}^\op`$
下から上の“逆行”の意味は:
- もとの圏 $`\cat{C}`$ 内では、$`a : A' \to A`$
- 反対圏 $`\cat{C}^\op`$ 内では、$`\o{a} : A \to A'`$
[/補足]
変数は、圏 $`\cat{C}`$ の対象または射を表すという暗黙の前提のもとで、6引数〈6変数 | 6項〉の関手を次のように書くと約束します。
$`\quad P(\o{A}, B, X, \o{Y}, R, \o{S})`$
関手の値だけではなくて、関手そのものもこの書き方で表します。この書き方は伝統的・前近代的なもので、次の点を注意する必要があります。
- 関手の値(特定の集合)と、関手そのものを区別していない。文脈により判断する。
- 引数変数は対象を表す変数(大文字)を使っているが、引数には射も許される(関手だから)。
- 引数変数が、圏 $`\cat{C}`$ の対象または射を表すことは暗黙化されている。
- 引数変数が共変か反変かはオーバーラインで区別するので、プロファイルの宣言はイチイチしない。
暗黙の前提や省略により曖昧となり、解読・解釈が困難にはなりますが、書く側にとってはとても楽ちんで便利です。このような“便利な書き方”は、古典テンソル計算の手法です。多引数〈多変数 | 多項〉の関手を「米田テンソル」と呼びたいのは、古典テンソル計算の手法を使う心積もりがあるからです。
古典テンソル計算と米田テンソル計算
古典テンソル計算では、添字〈インデックス〉を上下に振り分けます。ここで、「添字」とか「インデックス」は「引数〈argument〉」と同義語です。分野と伝統・習慣により違う呼び名を使っているだけで、意味的には同じことです。
前節の米田テンソルでは、オーバーライン記法で共変と反変の区別をしましたが、反変の引数変数〈添字 | インデックス〉を下側に、共変の引数変数を上側に書くと約束すると、オーバーラインは不要となります。
$`\quad P\left(
\begin{array}{l}
B, X, R
\\
A, Y, S
\end{array}
\right)
`$
これだと場所を取るので、引数変数〈添字 | インデックス〉を小さくして、引数達を囲む括弧は省略すると次のようになります。
$`\quad P^{B, X, R}_{A, Y, S}`$
さらに、引数達を区切るカンマも省略してしまうと:
$`\quad P^{B\, X\, R}_{A\, Y\, S}`$
非常にコンパクトに書けます。これが古典テンソル計算の標準的な記法です。
古典テンソル計算の記法で、米田テンソル $`P`$ の定義をもう一度書くと:
$`\quad P^{B\, X\, R}_{A\, Y\, S} := \cat{C}(A, R\times X)\times \cat{C}(S\times Y, B)`$
ところで、コエンドを使ったオプティックの議論は、下のようなストリング図を使って進めるのが効果的です(「圏論的レンズ 2: 具象オプティック」より)。
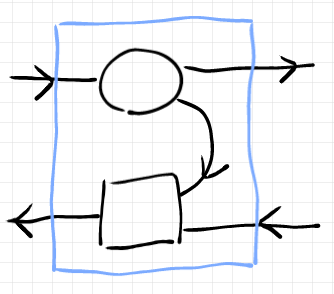
しかし、毎回ストリング図を描くのは大変なので、図だけでなくテキスト記法も欲しいのです。図の情報を律儀にテキストにエンコードすると、とても煩雑になります。テキトーにサボらないとやってられません。古典テンソル計算がサボる手法を提供してくれます。
米田テンソル計算の目的は、集合圏に値を持つ多引数〈多変数 | 多項〉関手の記述と計算を、古典テンソル計算にならった記法で行うことです。
過去(2021年)に、米田テンソル計算について述べています。
途中までしか書いてないので、古典テンソル計算にならった記法については説明していません。なので、(図ではなく)テキストによる記述と計算の説明もしたいと思っています。
なぜにまた米田テンソル計算
米田テンソル計算を考えるキッカケのひとつは、マリオ・ロマン〈Mario Román〉の論文 "Open Diagrams via Coend Calculus"(「米田テンソル計算 1: 経緯と発想」参照)です。最近、ロマンの論文をまた見る機会があって(ほとんど忘れている(苦笑)が)、「そう言えば、米田テンソル計算は中断していた」と思い出したわけです。
計算体系だけいじっていても面白くないので、レンズ/オプティック/フィードバック付き射などの圏をコエンド(テンソル計算の言葉では縮約)により構成する例を調べたいですね。
それと、コエンドによりホムセットを定義する際のストリング図と、ホムセットの要素(つまり射)のストリング図は無関係ではないのですが、どういう関係があるかハッキリしない。これがハッキリしたら楽しい気がします。
*1:大きな圏 $`\mbf{Set}`$ の上でコエンドを構成しているので、サイズの問題を考慮する必要があります。