「図式」「形状」という言葉は普通に使う日常語なので、テクニカルタームとして使うのはかえって難しいですね。が、使うことはけっこうあるので、ある程度は運用法を決めておきます。特にフォーカスするのは、「図式」「形状」が組み合わせ幾何的対象物〈combinatorial geometric object〉に対して使われる場合です。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\mfk}[1]{\mathfrak{#1}}
\newcommand{\In}{ \text{ in } }
\newcommand{\id}{\mathrm{id} }
\newcommand{\op}{\mathrm{op} }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\T}[1]{\text{#1} }
`$
内容:
図式 = 関手
Diag構成(「Diag構成: 圏論的構成法の包括的フレームワークとして」参照)の"Diag" は図式〈ダイアグラム | diagram〉のことです。ここでの図式は関手と同じです。関手それ自体を図形として扱うときや、極限・余極限と関連するときは、関手を図式と呼びます。ある文脈では、関手と図式は同義語です。関手の圏は図式の圏〈category of diagrams〉とも呼びます。
もちろん、ストリング図やペースティング図も図式です。なんらかのターゲット圏に描出〈rendering〉されたストリング図/ペースティング図は、関手(あるいは関手類似物)とみなせますが、描出する前の組合せ幾何的対象物も図式と呼ぶので、全体的に辻褄を合わせるのは難しいです。無理にコジツケないで、用語のコンフリクトが起きたと割り切ったほうが(少なくとも精神衛生上は)よいと思います。
関手を図式と呼ぶとき、関手の域圏〈domain category | source category〉は形状〈shape〉と呼ぶことがあります。極限の議論ならば、錐体〈cone〉の底面形状が出てきます。より組合せ幾何的香りが強い場合もあります -- そのときは「形状」と呼びたい気持ちが強くなります。そういう場合を次節以降で述べます。
組み合わせ幾何的対象物
冒頭と前節で、「組み合わせ幾何的対象物〈combinatorial geometric object〉」という言葉を使ったのですが、これはどんなモノを意味するのかを説明します。
厳密な定義があるわけでもないので、典型的な例を挙げます。以下の絵は、Wikipedia項目「複体」にある絵です。
この図は単体複体〈simplicial complex〉の例です。基本となる図形を組み合わせて作った図形です。この場合の“基本となる図形”は、点、線分、三角形、四面体です。“基本となる図形”が何個あるか目視で勘定してみましょう。
- 点(0次元単体と呼ぶ)が 18 個
- 線分(1次元単体と呼ぶ)が 23 本
- 三角形(内部を含む)(2次元単体と呼ぶ)が 8 面
- 四面体(内部を含む)(3次元単体と呼ぶ)が 1 個
以下は僕の手描きの絵ですが、二角形〈digon〉が混じった図形です。
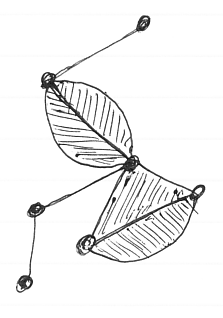
この場合の“基本となる図形”は、点、線分、二角形、三角形です。これも、“基本となる図形”が何個あるか目視で勘定してみましょう。
- 点が 7 個
- 線分が 10 本
- 二角形(内部を含む)が 3 面
- 三角形(内部を含む)が 1 面
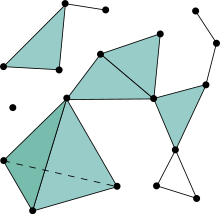
以下の図はまったく別な文脈(過去記事「スタック図の逆襲」)で出てくる図です。
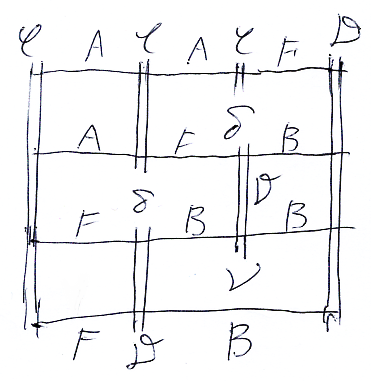
点が黒丸で描いてないので分かりにくいですが、“基本となる図形”は、点、縦線分(二重線)、横線分、四角形です。“基本となる図形”の個数は以下のとおりです。
- 点が 15 個
- 縦線分が 9 本
- 横線分が 11 本
- 四角形(内部を含む)が 6 面
“基本となる図形”の種類を形状ソート〈shape sort〉と呼ぶことにします。形状ソートに対して次元〈dimension〉が決まっています。上記の例達に出てきた形状ソートとその次元を列挙すると以下のようです。
- 点, 0次元
- 線分, 1次元
- 三角形, 2次元
- 四面体, 3次元
- 二角形, 2次元
- 縦線分, 1次元
- 横線分, 1次元
- 四角形, 2次元
最初の例(単体複体)では、各次元ごとに一種類の形状ソート、二番目の例では2次元の形状ソートが2つ(二種類の2次元図形)、三番目の例では1次元の形状ソートが2つ(二種類の1次元図形)でした。
いずれの場合でも、基本図形はセル〈cell〉と呼びます。この節の3つの例で、各形状ソートごとのセルが何個あるかを勘定しました。
セルには1次元低い境界がありますが、境界図形がどんなセルから構成されるか? は、形状ソートに対する規則として記述できます。
- 点の境界は、無い
- 線分の境界は、2個の点
- 三角形の境界は、3本の線分
- 四面体の境界は、4面の三角形
- 二角形の境界は、2本の線分
- 縦線分の境界は、2個の点
- 横線分の境界は、2個の点
- 四角形の境界は, 4本の線分(縦線分2本と横線分2本)*2
以上に述べたような、セル(基本となる図形)、セルを組み合わせた図形、セルの境界などの概念を系統的に整理するために形状付き集合〈shaped set〉という概念を使います。形状付き集合については、指標との関連において「指標の話: 形状の記述と形状付き集合」で述べています。先に過去記事を呼んでおくと理解がスムーズかも知れません。
オマケとしてもうひとつ、2008年の記事「おとぎ話としてのn-圏 -- 計算できる図形達の世界」の絵をそのまま再掲します。「球体集合達の圏の構文表示 1/2」においても同じ絵を参照しています。
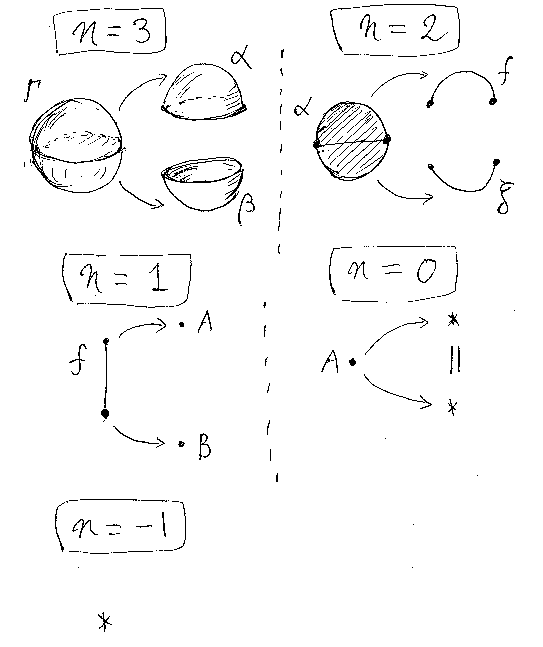
この絵は、n次元球体(n = 3, 2, 1, 0 の場合)の境界を絵に描いたものです。
- 3次元球体〈ボール〉の境界は、2面の2次元球体〈円板〉
- 2次元球体〈円板〉の境界は、2本の1次元球体〈線分〉
- 1次元球体〈線分〉の境界は、2個の0次元球体〈点〉
- 0次元球体〈点〉の境界は、無い(のだが、ダミーの(-1)次元球体を考えている)
(-1)次元球体は空集合ですが、次元が低い方から図形を組み立てていくときの初期状態として使うことがあります。「球体集合達の圏の構文表示 1/2」では、型理論的な演繹系を使って図形を組み立てています。このときの初期状態がダミーの(-1)次元球体です。
リーディ圏
「組合せ幾何的香りが強い場合」とは何かをハッキリと述べるために、リーディ圏〈Reedy category〉を紹介します。「指標の話: 形状の記述と形状付き集合」でリーディ圏を出していますが、定義は nLab を参照しているだけでした。
実は、形状付き集合のためにリーディ圏を準備するのはオーバースペックです。「リーディ圏」と呼ばれるある種の圏があるのだな、とだけ承知したうえで、この節を飛ばして次節に進んでも問題ありません。
リーディ圏は小さい圏 $`R`$ で、次の構造を持ちます。
- 広い部分圏 $`R_{+}`$
- 広い部分圏 $`R_{-}`$
- 次数関数 $`\mrm{deg} : |R| \to |\mbf{Odnl}|`$
$`\mbf{Odnl}`$ はすべての順序数からなる大きな圏です。$`R`$ は小さい圏なので、$`|R|`$ は小さい集合です。したがって、適当な順序数 $`\kappa \in |\mbf{Odnl}|`$ を取って、次数関数は次の形だとしてもかまいません。
$`\quad \mrm{deg} : |R| \to \kappa \In \mbf{Set}`$
次数関数の余域は議論に効いてこないので、どうでもいいです。多くの場合、普通の全順序を入れた自然数の集合を余域に取ります。
$`\quad \mrm{deg} : |R| \to \mbf{N} \In \mbf{Set}`$
次数関数 $`\mrm{deg}`$ により、圏 $`R`$ の射のクラス〈部分集合〉を以下のように決めます。後の都合から、リーディ圏の射はアロー〈arrow〉と呼びます。
- $`f\in \mrm{Mor}(R)`$ が、$`\mrm{deg}(\mrm{dom}(f)) \lt \mrm{deg}(\mrm{cod}(f))`$ を満たすとき、順行アロー〈direct arrow〉と呼ぶ。
- $`f\in \mrm{Mor}(R)`$ が、$`\mrm{deg}(\mrm{dom}(f)) \gt \mrm{deg}(\mrm{cod}(f))`$ を満たすとき、逆行アロー〈inverse arrow〉と呼ぶ。
リーディ圏の条件〈公理 | 法則〉は次です。
- $`\mrm{Mor}(R_{+})`$ の要素は、順行アローか恒等アロー〈恒等射〉である。
- $`\mrm{Mor}(R_{-})`$ の要素は、逆行アローか恒等アロー〈恒等射〉である。
順行アローの集合と逆行アローの集合は排他的なので、
$`\quad \mrm{Mor}(R_{+})\cap \mrm{Mor}(R_{-}) = \mrm{Id}(R)`$
です。$`\mrm{Id}(R)`$ は、恒等射だけからなる部分圏(離散圏)です。
リーディ圏の条件はもうひとつあって:
- $`R`$ の任意のアロー〈射〉は、$`R_{-}`$ のアローの後に $`R_{+}`$ のアローを結合した形に分解〈factorization*3〉できて、この分解(リーディ分解〈Reedy factorization〉、逆行・順行分解〈inverse-direct factorization〉)は一意的である。
上記の条件による $`f\in \mrm{Mor}(R)`$ の分解を $`f = f_{-}; f_{+}`$ と書きます。$`f_{-}`$ を $`f`$ の逆行成分〈inverse factor | 逆行因子〉、$`f_{+}`$ を $`f`$ の順行成分〈direct factor | 順行因子〉と呼びます。逆行成分か順行成分のどちらかが恒等アローかも知れません。両方の成分が恒等アローなら、もとのアローが恒等アローです。
リーディ圏のなかで特に扱いやすいものとして:
- $`R = R_{+}`$ であるリーディ圏を順行リーディ圏〈direct Reedy category〉と呼ぶ。
- $`R = R_{-}`$ であるリーディ圏を逆行リーディ圏〈inverse Reedy category〉と呼ぶ。
順行リーディ圏または逆行リーディ圏における逆行・順行分解は、どちらかの因子が恒等アローという意味で自明になります。
余談ですが、リーディ圏は、「パチモンの圏 = システム」の意味でパチモンの圏です。リーディ圏と圏同型な圏はリーディ圏になりますが、圏同値な圏がリーディ圏になるとは限らないからです。
リーディ圏の例
リーディ圏 $`R`$ を域とする共変関手 $`X:R \to \mbf{Set}`$ あるいは反変関手 $`X: R^\op \to \mbf{Set}`$ は、組合せ幾何的対象物(組み合わせ構造を持つ図形)とみなされます。あるいは同じことですが、組合せ幾何的対象物はリーディ圏からの集合圏への関手〈図式〉として記述されます。そのことが、この記事で言いたいことです。
リーディ圏の定義に出てくる次数関数を次元関数〈dimension function〉とも呼び、$`\mrm{dim}`$ とも書きます。呼び名は何でもいいのですが、組合せ幾何的対象物を扱うときは「次元」がふさわしいと思います。リーディ圏の対象を形状ソート〈shape sort〉、あるいは単にソート〈sort〉と呼びます。前々節で非形式的〈雰囲気的〉に定義した形状ソートの対応物としてリーディ圏の対象を考えるからです。
単体圏〈simplex category〉や球体圏〈globe category〉が典型的なリーディ圏ですが、ここでは以下の2つの圏を事例に使います。
- 1次元(までの)球体圏 $`\mbf{g1}`$
- 矩形圏〈rectangle category〉 $`\mbf{r2}`$
どちらのリーディ圏も、有限個の対象〈形状ソート〉と射〈アロー〉しか持ちません。
- $`\mbf{g1}`$ は、2個の形状ソートと、恒等アロー以外に2本の順行アロー(次元が上がるアロー)
- $`\mbf{r2}`$ は、4個の形状ソートと、恒等アロー以外に12本の順行アロー(次元が上がるアロー)
対象〈形状ソート〉と射〈アロー〉を列挙します。「おやっ?」「奇妙だ」と思うかもしれませんが、とりあえず定義はそのまま受け取ってください。
- $`\mbf{g1}`$ の対象 $`= \{0, 1\}`$
- $`\mbf{g1}`$ の射(恒等射以外)
- $`s: 0 \to 1`$
- $`t: 0 \to 1`$
- $`\mbf{r2}`$ の対象 $`= \{O, V, H, D\}`$
- $`\mbf{r2}`$ の射(恒等射以外)
- $`sDV: V \to D`$
- $`tDV: V \to D`$
- $`sDH: H \to D`$
- $`tDH: H \to D`$
- $`sVO: O \to V`$
- $`tVO: O \to V`$
- $`sHO: O \to H`$
- $`tHO: O \to H`$
- $`sDV;sVO: O \to D`$
- $`sDV;tVO: O \to D`$
- $`sDH;sHO: O \to D`$
- $`sDH;tHO: O \to D`$
対象〈形状ソート〉に対する次元関数は次のよです。
- $`\mbf{g1}`$ の次元関数
- $`\mrm{dim}(0) = 0`$
- $`\mrm{dim}(1) = 1`$
- $`\mbf{r2}`$ の次元関数
- $`\mrm{dim}(O) = 0`$
- $`\mrm{dim}(V) = 1`$
- $`\mrm{dim}(H) = 1`$
- $`\mrm{dim}(D) = 2`$
リーディ圏 $`\mbf{g1}`$ は、グラフ〈有向グラフ | {directed}? graph〉という組み合わせ幾何的対象物を記述するための圏です。リーディ圏 $`\mbf{r2}`$ は、二重圏の台構造〈{underlying | carrier } structure〉となる組み合わせ幾何的対象物です。二重圏に関しては、過去記事「二重圏、縦横をもう一度」を参照してください。
$`\mbf{g1}, \mbf{r2}`$ のアロー〈射〉は、セルの境界を記述するために使うのですが、「なんで次元が上がるアローなんだ? 逆ではないか」と訝しく思うかも知れません。それは次節で説明します。
反変関手が主流
組み合わせ幾何的対象物は、リーディ圏から集合圏への関手〈図式〉として記述するのですが、反変関手を使うほうが多数派なのです。例えば、グラフ〈有向グラフ〉は、次の関手だと考えます。
$`\quad X: \mbf{g1}^\op \to \mbf{Set} \In \mbf{CAT}`$
反変関手なので、次のようになります。
- $`X(0) \in |\mbf{Set}|`$
- $`X(1) \in |\mbf{Set}|`$
- $`X(s): X(1) \to X(0) \In \mbf{Set}`$
- $`X(t): X(1) \to X(0) \In \mbf{Set}`$
$`\mbf{g1}`$ 内のアロー $`s`$ は $`s: 0 \to 1`$ ですが、反変関手 $`X`$ で移された先では $`X(s): X(1) \to X(0)`$ なので次元が下がる方向の射なのです。ややこしい。このややこしさは、用語や記法にも(悪い)影響があります。
一般に、セルにその境界(の一部)を構成するセルを対応させる写像を面写像〈face map〉と呼びます。面写像は、反変関手の域であるリーディ圏のアローに由来します。“リーディ圏側のアロー”と対応する“集合圏側の写像〈関数〉”をそれぞれ何と呼ぶか? 2つの流儀があります。
- リーディ圏のアローは、余面アロー〈coface arrow〉と呼ぶ。余面アローの反変関手による像〈値〉が面写像
- リーディ圏のアローも、面アロー〈face arrow〉と呼ぶ。面アローの反変関手による像〈値〉が面写像
ここでは、余面アローを使います。
$`\quad \mrm{Mor}(\T{リーディ圏}) \ni \T{余面アロー} \mapsto \T{面写像}\in \mrm{Mor}(\T{集合圏})`$
用語の運用をもう少し詳しく説明すると:
- 反変関手の域であるリーディ圏の、生成射(射の集合の生成元)である、次元を1つ上げるアローを、余面アロー〈coface arrow〉と呼ぶ。
- 余面アローの反変関手の像である、集合圏の射〈写像 | 関数〉を面写像〈face map〉と呼ぶ。
- 反変関手の域であるリーディ圏の、生成射(射の集合の生成元)である、次元を1つ下げるアローを、余退化アロー〈codegeneracy arrow〉と呼ぶ。
- 余退化アローの反変関手の像である、集合圏の射〈写像 | 関数〉を退化写像〈degeneracy map〉と呼ぶ。
今回の2つの例では、余面アローと面写像しか出てきません。余退化アロー/退化写像は使ってません。
リーディ圏からの反変関手による像〈値〉 $`X(s)`$ はしばしば $`s^*`$ と略記します。
$`\quad s^* : X(1) \to X(0) \In \mbf{Set}`$
上付きアスタリスクは反変であることを示していますが、アスタリスクも省略してしまうケースもあります。
$`\quad s : X(1) \to X(0) \In \mbf{Set}`$
こうなると、$`s`$ が関手の域側か余域側かも($`s`$ だけ見ても)分からないので解釈に難儀するでしょう。次の点を文脈から確認して下さい。
- 反変関手(多数派)を使っているのか? それとも共変関手(少数派)を使っているのか?
- 関手の域側の射と対応する余域側の射をどのように表記しているか?
形状付き集合
集合圏への関手〈図式〉が組み合わせ幾何的対象物を表す状況では、その関手〈図式〉を形状付き集合〈shaped set〉と呼びます。関手が反変のときも共変のときもありますが、ここでは、多数派である反変関手(前層〈presheaf〉とも呼ぶ)を使うとします。
形状付き集合〈前層〉の域である圏を形状圏〈shape category〉、形状スキーマ〈shape schema〉、あるいは単に形状〈shape〉と呼びます。
複数の形状スキーマや、形状スキーマのあいだの関手を考えることがあります。すると、形状スキーマを対象とする圏が出現します。形状スキーマを対象とする圏(0-圏 = 集合のときも、2-圏のときもある)は形状ドクトリン〈shape doctrine〉と呼ぶことにします。
「形状」「形状圏」という言葉が以下のどれを指すかわからない、あるいは混同・混乱している状況が生じがちなので注意して下さい。
- 形状スキーマを対象とする圏である形状ドクトリン
- 形状ドクトリンの対象である、形状ソートを対象とする圏である形状スキーマ
- 形状スキーマの対象である、形状ソート
また、形状ソート(形状スキーマの対象)と、図式による像〈値〉である集合(集合圏の対象)も混同されることがあります。形状ソートの像である集合の要素がセル〈cell〉です。形状スキーマにはセルという概念がありません。
記法の一案
混同・混乱しがちな概念が出てくるので、文字種・フォントにより区別したほうがいいでしょう。スピヴァック〈David I. Spivak〉達が使っていた記法・用語も参考に一案を考えました。
- 形状スキーマ(を表す変数)はフラクトゥール体のラテン文字小文字で書く。$`\mfk{c}, \mfk{s}`$ など。
- 形状スキーマの対象である形状ソート(を表す変数)はギリシャ文字小文字で書く。$`\alpha, \beta, \xi`$ など。
- 次元関数の値となる次元〈自然数〉(を表す変数)はラテン文字小文字で書く。$`n, m, k`$ など。
- 形状ソートとその次元をペアにして $`(\alpha, n)`$ のように書く。
- 形状付き集合(を表す変数)はラテン文字大文字で書く。$`X, Y, A`$ など。
- 形状付き集合(実体は関手) $`X`$ の値である集合 $`X(\alpha)`$ を $`X_\alpha`$ とも書く。形状ソートの次元も明示したいときは $`X_{\alpha, n}`$ と書く。
- 形状付き集合(実体は関手) $`X`$ の値である写像 $`X(f)`$ を $`f^*_X`$ と書く。
- $`f^*_X`$ に別な名前を付けてもよい。
例えば、グラフ〈有向グラフ〉は、リーディ圏 $`\mbf{g1}`$ を形状スキーマとする反変の形状付き集合です。スピヴァック〈David I. Spivak〉達のハイフンを使う記法で書くなら:
$`\quad \mbf{Graph} := \mbf{g1}^{\op}\T{-}\mbf{Set} = [\mbf{g1}^{\op}, \mbf{Set}]`$
形状スキーマ $`\mbf{g1}`$ では、形状ソートとその次元が一致していますが、冗長になるのをかまわずに書けば:
- 形状ソート $`(0, 0)`$ に対する $`X`$ のセルの集合は $`X_{0, 0}`$ 。$`(0, 0)`$-セルは頂点〈vertex〉とも呼ぶ。
- 形状ソート $`(1, 1)`$ に対する $`X`$ のセルの集合は $`X_{1, 1}`$ 。$`(1, 1)`$-セルは辺〈edge〉とも呼ぶ。
- 余面アロー $`s: 0 \to 1`$ に対する $`X`$ の面写像は $`s^*_X : X_{1, 1} \to X_{0, 0}`$ 。ソース写像〈source map〉とも呼ぶ。
- 余面アロー $`t: 0 \to 1`$ に対する $`X`$ の面写像は $`t^*_X : X_{1, 1} \to X_{0, 0}`$ 。ターゲット写像〈source map〉とも呼ぶ。
グラフの圏 $`\mbf{Graph}`$ の射は、反変関手〈前層〉の圏の射なので、実体は自然変換です。
矩形圏と矩形集合
リーディ圏 $`\mbf{r2}`$ は矩形圏〈rectangle category〉でした。矩形圏を形状スキーマとする(反変の)形状付き集合は、$`\mbf{r2}^\op`$-形状付き集合〈$`\mbf{r2}^\op`$-shaped set〉です。これを短く矩形集合〈rectangular set〉と呼びます。このネーミングは、単体圏/単体集合、球体圏/球体集合などと同じルールです。
ハイフンを使う記法で書くなら:
$`\quad \mbf{r2Set} := \mbf{r2}^{\op}\T{-}\mbf{Set} = [\mbf{r2}^{\op}, \mbf{Set}]`$
形状スキーマ $`\mbf{r2}`$ に関しては:
- 形状ソート $`(O, 0)`$ に対する $`X`$ のセルの集合は $`X_{O, 0}`$ 。二重圏の文脈では、$`(O, 0)`$-セルは対象〈object〉とも呼ぶ。
- 形状ソート $`(V, 1)`$ に対する $`X`$ のセルの集合は $`X_{V, 1}`$ 。二重圏の文脈では、$`(V, 1)`$-セルは縦射〈vertical morphism〉とも呼ぶ*4。
- 形状ソート $`(H, 1)`$ に対する $`X`$ のセルの集合は $`X_{H, 1}`$ 。二重圏の文脈では、$`(H, 1)`$-セルは横射〈horizontal morphism〉とも呼ぶ。
- 余面アロー $`sDV: V \to D`$ に対する $`X`$ の面写像は $`{sDV}^*_X : X_{D, 2} \to X_{V, 1}`$ 。二重圏の文脈では、二重セル〈double cell〉の左フレーム写像〈left frame map〉とも呼ぶ。
- (以下省略)
矩形集合は二重圏の下部構造になっています。上部構造である二重圏の用語を拝借して面写像に名前を付けることができますが、一般的な形状付き集合の面写像達にそれらしい名前を付けることは無理です。味気ない番号・符丁で呼ぶしかないでしょう。
おわりに
モノイドや群のような代数系は、集合の上に演算と法則を載せています。それに対して、圏、二重圏、さまざまな種類の高次圏は、形状付き集合の上に演算と法則を載せています。したがって、土台となる形状付き集合を把握しておく必要があります。この記事で述べたように、形状付き集合は意外に複雑な概念であり、異なったレベルの構成素を混同しがちです。混同しないように整理しておきましょう。
*1:画像は https://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Simplicial_complex_example.svg/220px-Simplicial_complex_example.svg.png
*2:[追記]この絵の線分はパス(基本線分を繋いだモノ)も含まれますね。境界が基本図形になるとは限りません。例えば、「ペースティング図、コンピュータッド、ストリング図」参照。[/追記]
*3:"factorisation" の綴りのほうが多いかも。
*4:「縦横」を使うのは好ましくないのですが、今ここではいいとします。