このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

衝撃的なデータベース理論・関手的データモデル 入門

雑記／備忘

デイヴィッド・スピヴァックによる衝撃的なデータベース理論である関手的データモデル。どうしたらうまく説明できるか？ と色々と悩んでしまいますが、まー、書けるところから書き始めてしまいましょう。

さー、いらっしゃい、いらっしゃい。関手的データモデルの世界へようこそ。圏論の言葉は出てきますが、圏論の予備知識はほぼゼロでOKですよ。

[追記 date="翌日"]取り急ぎ勢いで書きましたので、不注意と早とちりが混じっていました。追記と取り消し線の形で訂正と注記を足しました。字句レベルの表現の変更は直接編集しています。

あとそれと、圏論の基本用語を知りたいときはコチラ、… って、……、ゴメン！[/追記]

内容：

  1. はじめに
  2. 本の購入のサンプル
  3. スキーマのグラフ表現
  4. キーとか計算カラムとか
  5. 圏としてのスキーマ
  6. 関手としてのデータベース状態
  7. テーブルの変化
  8. 自然変換としてのデータ操作
  9. データベースに圏論が使い放題

はじめに

関手的データモデルでは、ものごとを徹底的に単純化します。現実世界との対応の適切性、運用の容易性など、価値判断を伴う議論はしません（それは別なタイミングでしてください）。理論的な夾雑物を容赦なく取り除きます。曖昧で衒学的なウンチクなんてもってのほか！ その結果、データベースの原理や常識だと思われているかなりの部分が無意味化します。

  1. テーブルとドメイン（原子的値の領域）の区別はしない。
  2. 第一正規形という概念はない。「原子的な値」という概念がないのでナンセンスとなる。
  3. 主キー、外部キーといった概念は単なる手段／トリックであって、本質的ではない。
  4. 従属性（依存性）とビジネスルール、その他の制約を区別しないで一様に扱う。
  5. テーブルは集合と考えてよいが、その要素がタプルである必要はない。つまり、テーブル（のインスタンス）を直積の部分集合とは考えない。
  6. 諸々の有限性を前提とはしない。必要なときだけ有限性を仮定する。

今回の説明では部分写像（partial map）を使うので次の点も注意しておきます。

  • undefinedの意味のNULLは遠慮なく使う。ただし、「NULL」ではなくて記号「⊥」を使って表す。

以下で、簡単なサンプルスキーマを提示して、それを、“集合と部分写像の圏”で解釈します。

本の購入のサンプル

「人が本を購入する」ことをモデル化します。テーブルは、Person（人）、Book（本）、Purchase（購入）の3つとします。データ型にStringとIntegerがあるとして、これらは名前から想像されるお馴染みの意味を持つとしましょう（細かい話は割愛）。他に、生年月日の日付用にYMDというデータ型も使いますが、これはIntegerの3つ組タプルの型だとします。あと、DateTimeはYMDより精密な（秒数までとかの）時刻です。

テーブルスキーマの記述は仮に次の形を使うとします。



table Person {

  // 人の名前

  name: String,
  // 人の生年月日

  birth: YMD

};

JSONみたいな形で、見りゃわかるでしょ。nameとbirthが、Personテーブルのカラムです。YMDはタプル型だから第一正規形じゃないって？ だーから、そんなことはドーデモイイの。

人に番号を付けて主キーにしたほうがいいって？ そのほうが確かに便利そうですが、今回はそれもナシとします。そういうワザは必須なものではないので*1。

データ型（ドメイン）とテーブルは区別しないので、StringとYMDも“テーブル”です。Person同様にtableとして宣言しておきましょう。



table String {};
table YMD {};

「Stringがtable」って、言葉としては違和感があるでしょうが、どうか気にしないで。どうしても気になるなら、どうせ集合が割り当てられるんだから set とかのキーワードにして、set Person、set String とかに読み替えてください。Stringにはカラムがないので {} です。YMDにもカラムがありません。Y（year）、M（month）、D（day）を取り出すカラムがあるだろう、って？ ないです。このスキーマ内ではないです。スキーマが解釈される先の世界*2には、Y, M, D を取り出す写像があるでしょうがね。

StringとYMDの宣言には、fixedってキーワードを付けておきます。



fixed table String {};
fixed table YMD {};

fixedの意味は、このスキーマが運用される以前に、テーブルの意味となる集合を固定してしまうことを指示します。fixedでないテーブルは、時間に従って内容（集合）が変化します。

スキーマの続きを書いてしまいましょう。



fixed table String {};
fixed table YMD {};
table Person {

  name: String,

  birth: YMD

};
fixed table Integer {};
table Book {

  isbn: Integer

};
fixed table DateTime {};
table Purchase {

  person: Person,

  book: Book,

  dateTime: DateTime,

};

ISBNは整数か？ とか、同じ本をまとめ買いできない、とかの突っ込みどころはあるでしょうが、ほとんどドーデモイイことでしょう。まとめ買いは、同じレコードを冊数分入れちゃう方法があります -- 一部の人から毛嫌いされている重複を許す集合（バッグ、マルチセット）ですが、クライスリ構成（という圏論の手法）を使えば普通に定式化できます。

スキーマのグラフ表現

カラムは圏の射（とりあえず矢印と思ってね）と考えるので、圏論の記法では例えばnameカラムは、name:Person→String のようになります。今回は、カラム名に重複はありませんが、同名のカラムが出てきてしまったなら、Person.name:Person→String のようにテーブル名とドットで修飾すればいいでしょう。これも別にドーデモイイ話ですけど*3。

さて、圏は対象と射からなるので、有向グラフで図示できます。今回のスキーマに出てくる頂点（ノード、バーテックス）は {String, YMD, Person, Integer, Book, DateTime, Purchase} で、それらのあいだを結ぶ辺（エッジ、アーク）は次のとおりです。大文字小文字の違いに注意してください。

  1. name:Person→String
  2. birth:Person→YMD
  3. isbn:Book→Integer
  4. person:Purchase→Person
  5. book:Purchase→Book
  6. dateTime:Purchase→DateTime

とりあえずは、圏の対象とは頂点のこと、圏の射とは辺のことだと思ってください。CatyのGraphVizコマンドで図に描いてみました。fixedなノードは水色、そうでないノードはピンクにしました。

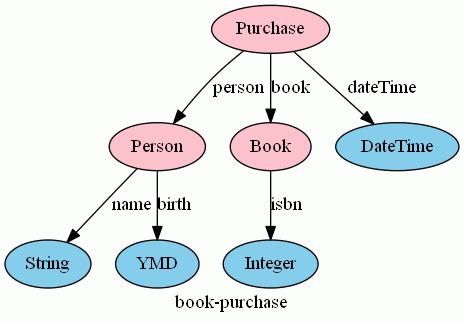
ツリーの形になっているのは特に意味はありません（たまたま、そうなってしまった）。この図を描くCatyScriptソースコードは次：



// this is CatyScript

[

  gv:node --style=filled --fillcolor=skyblue String,

  gv:node --style=filled --fillcolor=skyblue YMD,

  gv:node --style=filled --fillcolor=pink    Person,

  gv:node --style=filled --fillcolor=skyblue Integer,

  gv:node --style=filled --fillcolor=pink    Book,

  gv:node --style=filled --fillcolor=skyblue DateTime,

  gv:node --style=filled --fillcolor=pink    Purchase,
  gv:edge --label=name     Person   String,

  gv:edge --label=birth    Person   YMD,

  gv:edge --label=isbn     Book     Integer,

  gv:edge --label=person   Purchase Person,

  gv:edge --label=book     Purchase Book,

  gv:edge --label=dateTime Purchase DateTime,

] | gv:graph --label=book-perchase

キーとか計算カラムとか

どうしても気になってしまう人がいるかもしれないので、主キー／外部キー、従属性などにチラリと触れておきます。

いま、人（person）になんらかの番号を付けて、それをnumカラムで取り出せるとしましょう。idカラムと命名したいところですが、idは圏論的な意味で（恒等射として）使うので、num:Person→Integer とします。numの実現には、「全域写像であり単射になる」という条件を課すことにします。この全域単射性の条件を付けて特定されたカラムが主キーです（単一キーと複合キーの区別はないです）。

一般に、f:A→B が単射な部分写像*4のとき、fは「おおむね可逆」となります。おおむね可逆（厳密に定義可能な言葉）とは、部分写像 g:B→A があって、「f;g と g;f が、定義される範囲では恒等写像と一致する」ことです。おおむね可逆な部分写像fの"おおむね逆写像”を、f~1 （f-1 と似てるが微妙に違う記法）と書くことにします。

num:Person→Integer は単射、ゆえに、おおむね逆写像 num~1 が存在して、num;num~1 = idPerson が成立します。person:Purchase→Person とは別に、外部キーに相当する写像を personNum:Purchase→Integer とすると、次の等式が成立しているはずです。

  • person = personNum;num~1 : Purchase→Person

このような等式を、スピヴァックはパス同値関係（path equivalence relation）と呼び、あらゆる制約をパス同値関係で表現しています。パス同値関係を圏論の言葉で言えば可換図式*5で、上のケースでは、person, personNum, num~1 を3辺とする三角形が可換（2つの経路のどっちをたどっても結果が同じ）となります。

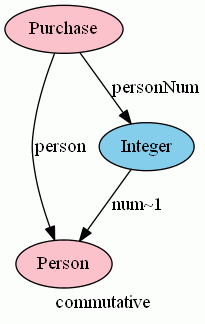
さて、生年月日から年齢を計算する関数（写像）を calcAge:YMD→Integer とします。もちろん、calcAgeには「現在の日時」という暗黙のパラメータがありますが、それは省略しています。Personのageカラムを、birth;calcAge という写像の結合（composition）として定義すると、この定義自体が次の等式となります。

  • age = birth;calcAge : Person→Integer

これも可換な三角形を形成しますね。

num, num~1, personNum, calcAge, age も入れたグラフは次のようになります。

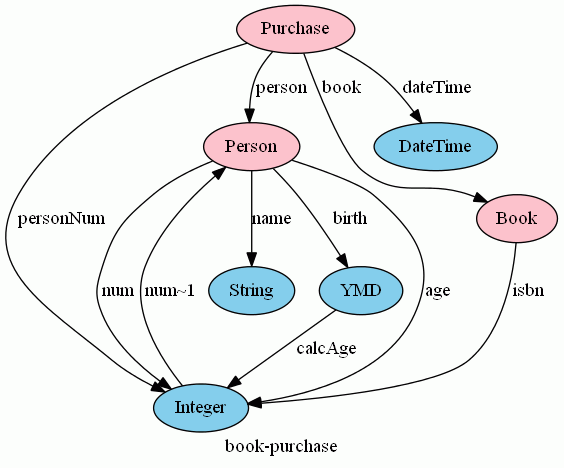
この図には明示されてませんが、次のような等式／不等式が課されていることをもう一度注意しておきます。

  1. num;num~1 = idPerson : Person→Person
  2. num~1;num ⊆ idInteger : Integer→Integer
  3. person = personNum;num~1 : Purchase→Person
  4. age = birth;calcAge : Person→Integer

person:Purchase→Person という写像を、 主キーnumと外部キーpersonNumを使って personNum;num~1 と表現するのは、単なる代替手段だと分かるでしょう。こういうトリックは、使わなくて済むなら使わないほうが直接的で分かりやすいのです*6。

[追記]age:Person→Integer は、計算によって値が得られるカラムの例として出しましたが、スキーマを構成する正式なカラム（射）ではありません。[/追記]

圏としてのスキーマ

ここまで、スキーマの意味論を先取りして、「テーブルは集合、カラムは部分写像」であるかのように説明してきましたが、これは正確ではありません。スキーマ自体は純粋に記号的な構造物です。「スキーマとは単なる有向グラフだ」と考えれば十分ですが、もう一歩進めて「スキーマとは圏だ」とみなすと圏論へと繋がります。いちおう、圏としてのスキーマの話をしますが、この節は若干の予備知識を仮定しているので、分かりにくかったら「スキーマとは単なる有向グラフだ」という理解でかまいません。

有向グラフGがあって、Gの頂点にも辺にもラベル（名前）が付いていて、頂点／辺はラベルで識別できるとします。この仮定のもと、頂点／辺それ自体とそのラベルを同一視します。

Gの頂点と辺が"互い違い”に現れる列をパスと呼びます。ただし、パスは次の条件を満たします。

  1. 最低でも頂点が2回は現れる。
  2. 最初と最後は頂点である。
  3. 隣り合って出現する頂点と辺は接合している。

例題である「本の購入」のグラフ（二番目のほう）に関して、[Purchase, person, Person, birth, YMD, calcAge, Integer] とか [Integer, num~1, Person, name, String] などはパスです。（ぜひ指でたどってみてください。）[Person, Person] もパスになります。[Book, isbn, Integer, num~1, Person, birth, YMD] は、現実的な意味はないのですがパスになります。

有向グラフGのパスの全体をPath(G)とすると、次のようにして圏Cを構成できます。（「モノイドと有向グラフから圏を構成する」にも記述あり。）

  1. |C| := (Gの頂点の集合)
  2. Mor(C) := Path(G)
  3. f∈Mor(C) に対して、dom(f) := (パスの最初の頂点), cod(f) := (パスの最後の頂点)
  4. A∈|C| に対して、idA := [A, A]
  5. 射の結合は、パスのしりとり風の連接

以上の手順で作った圏はグラフGから生成された自由圏と呼びます。データベーススキーマの場合は、有向グラフ以外に制約条件（パス同値関係）があるので、それらも考慮して圏を作ります*7。

有向グラフと制約条件の組は、圏の表示（presentation）と呼びます。ベクトル空間の基底や、「生成元と関係」による代数系の定義をご存知の方は、圏の表示も同じようなモノだと思ってください。有限グラフと有限個の制約条件からなる表示は有限表示と呼ばれます。有限表示を持つ圏は、組み合わせ的／計算的（combinatorial/computational）に扱うことができます。

具体的な記述や計算では表示が必要になるので、データベーススキーマは表示付きの圏、あるいは圏の表示がスキーマなのだと思ってもかまいません。以下では、圏そのものより、圏の表示であるグラフ（＋制約条件）をスキーマとみなして説明します。

関手としてのデータベース状態

スキーマは、それ自体は有向グラフ、つまり、丸と矢印からなる図形に過ぎません。データベースとしての意味を与えるために次の割り当てをします。

  1. グラフの頂点には集合を割り当てる。
  2. グラフの辺には集合のあいだの部分写像を割り当てる。

グラフの頂点がテーブルで、グラフの辺がカラムだったので：

  1. テーブル（の名前）には集合を割り当てる。
  2. カラム（の名前）には集合のあいだの部分写像を割り当てる。

ですね。ここで部分写像 f:A→B とは、Aの部分集合X上で定義された写像のことです。X = A のときもあるし、Xが空のときもあります。部分写像の結合（composition）は、定義できる範囲で、しかし出来るだけ頑張って行います。集合と部分写像からなる体系（圏ですが）をPartialと書きます。

上記のような、「テーブルに集合、カラムに部分写像」という割り当てを、データベース状態とかデータベースインスタンスと呼びます。誤解の心配がなければ、単にデータと呼んでもいいでしょう。

[追記]スピヴァックのオリジナルの定義は、PartialではなくてSetを使っています。つまり、未定義としてのNULLを認めない立場です。ただし、Set以外はダメということではなくて、スピヴァック自身もSet以外の圏を使っています。僕がPartialを選んだ理由は「関手的データモデルをどう説明するか？ 考えてます」に書いてあります。[/追記]

データベーススキーマSに対して、そのデータベース状態を D:S→Partial のように書きます。テーブル名にテーブルの内容である集合、カラム名にその実現である部分写像を対応させているので、写像と同じ記法を使います。この手の対応は、圏論では関手（functor）と呼びます。したがって、

  • データベース状態は関手である

となります。これが関手的データモデル（functorial data model）という名前の由来です。短い標語にするなら「データ＝関手」。

スキーマS上のデータベース状態は（普通は）たくさんあります。ある一時点を取ればひとつの関手 D:S→Partial が定まります。別な時点では別な関手 D':S→Partial となるでしょう。データベース状態は時々刻々と変化します。

しかし、変化しないほうがよいテーブル／カラムもあります。例えば、今回の例題に出てくるStringやIntegerが、時々刻々と変化するのはハナハダ迷惑です。スキーマにおけるtable宣言でfixed（仮の記法ですが）と付けて*8、水色で図示しているテーブルは変化しないほうが望ましいのです。ただし、「変化する／しない」も相対的なものです。例えば、アスキー文字だけを許すStringだったのが、それでは不便なのでユニコードをサポートするように変化することもあるでしょう。Stringでサポートする文字範囲が時々刻々と変化することがないとも言えません。

実際は、次のようなことです。

  • 割り当てられる集合が比較的変化しにくい名前はデータ型の名前（例えばString）と考える。
  • 割り当てられる集合が頻繁に変化する名前は常識的な意味でのテーブルの名前（例えばPerson）と考える。

テーブルの変化

我々のサンプルでは、時々刻々と変化するのは、Person, Book, Purchaseの3つのテーブルです（図ではピンクのノード）。Personは会員名簿のようなものなので、増えたり減ったりするでしょう。Bookはドンドン増えそうですが、本が絶版になれば減ります。Purchaseは、過去ログを捨てなければ増える一方の記録です。

[追記]今回の簡単なサンプルでも、安易にレコードを削除すると整合性が保てなくなります。この辺のことは、また機会をあらためて述べたいと思います。[/追記]

Personテーブルに注目するとして、とあるデータベース状態Dと別なデータベース状態D'でPersonテーブルが変化したとします。テーブル内容（集合）をJSONリテラルを使って表記するとします。一番外側の中括弧（{, }）は集合を表す括弧です。

D(Person) = {
  {"name": "板東トン吉", "birth": [1985, 10, 1]}, 
  {"name": "大垣ペケ子", "birth": [1991, 6, 23]}
}

D'(Person) = {
  {"name": "大垣ペケ子", "birth": [1991, 6, 23]}, 
  {"name": "小宮山ガン太", "birth": [1967, 3, 7]}
}

まー、見比べればどう変化したか分かってしまうのですが、念のため、μ:D(Person)→D'(Person) という部分写像で変化を明確化しておきます。記述の単純化のため、人の名前だけで部分写像μを記述します。

  • μ("坂東トン吉") = ⊥
  • μ("大垣ペケ子") = "大垣ペケ子"

⊥は未定義を表す記号です。この部分写像 μ:D(Person)→D'(Person) は次の事実を表現します。

  1. "坂東トン吉" のレコードは削除された。
  2. "大垣ペケ子" のレコードはそのまま。
  3. "小宮山ガン太" のレコードは追加された。

[追記]テーブルの変化は、レコードの追加／削除のみで、SQLのUPDATE文のような変更は別に扱うべきでした。この節の残りの記述は、その観点から訂正しました。[/追記]

現実的な例だとかえって分かりにくいかもしれないので、μ:{1, 2, 3, 4} → {2, 4, 5} としてみましょう。

  • μ(1) = ⊥
  • μ(2) = 2
  • μ(3) = ⊥
  • μ(4) = 4

これは次の変化を記述します。

  1. もとの1は削除された。
  2. もとの2はそのまま。
  3. もとの3は4に変化した（更新された）削除された。
  4. もとの4はそのまま。
  5. 5が追加された。

部分写像で変化を記述する一般的なルールは次のようになります。X⊆A を定義域とする部分単射写像 f:A→B があるとき：

  • Xに属さないAの要素は削除されたとみなす。
  • f(a) = b のとき、aがbに変化した（更新された） aとbは（異なる時点における）同じものとみなす。
  • fの像に属さないBの要素は新たに追加されたとみなす。

単射の条件を付けないときは：

  • a≠a' で f(a) = f(a') = b のとき、aとa'はマージされてbになったとみなす。

自然変換としてのデータ操作

[追記]「更新」という言葉は、SQLのUPDATE操作を連想するので、「変更」に置換しました。[/追記] [追記の追記]SQLのUPDATE文のような操作（個別のレコードに対する変更）は、だいたい分かったけど、それを書く気力が溜まるまでに時間がかかるかも。[/追記の追記]

前節の μ:D(Person)→D'(Person) はテーブルPersonの変化を記述します。1つのテーブルだけではなくて、データベースに属する複数のテーブルが同時に変更されることがあるかもしれません。例えば、PersonとPurchaseが同時に変更されるとき、次の2つのμを使います。

  • μPerson:D(Person)→D'(Person)
  • μPurchase:D(Purchase)→D'(Purchase)

Bookには何の変化がないとしても、μBook = idBook （Bookの集合上の恒等写像）だとして次のように書けます。

  • μBook:D(Book)→D'(Book)

StringやIntegerに対しても同様に恒等写像を μString, μInteger として採用できます。その結果、すべてのテーブルXに対して、μX:D(X)→D'(X) が定義できることになります。

{μPerson, μPurchase, μBook, μString, μInteger, ...} は、すべてのテーブルに対する変更を束ねたもので、データベース全体への操作の表現となっています。テーブルで目印を付けられた部分写像の束（たば） {μX | Xはテーブル} は、圏論では関手のあいだの自然変換と呼ばれるものです。

実は、テーブル変更の集まりが自然変換であるためには条件が付きます。c:S→T がスキーマに現れるテーブルとカラムのとき、次の等式を満たす必要があります。

  • D(c);μT = μS;D'(c) : D(S)→D'(T)

具体例をひとつ挙げると：

  • D(person);μPerson = μPurchase;D'(person) : D(Purchase)→D'(Person)

これは次の意味を持ちます。

  • 古いPurchaseテーブルのpersonカラムの値（Personレコード）の変更写像μの結果は、Purchaseテーブルの変更写像μの結果に対するpersonカラムの値に等しい。

つまり、変更前後で整合性が保たれるための制約条件になっています。この制約条件を、圏論では可換図式という形で書くのが普通です。

D(S) -- D(c) --> D(T)
 |               |
 |μ_S           |μ_T
 |               |
 v               v
D'(S) - D'(c) -> D'(T)

従属性（依存性）、ビジネスルール、データ操作時の整合性などの様々な制約が、すべて一律に可換図式によって表現できます。可換図式の一般化である高次セルを使うと、より柔軟で多様な制約記述ができます。

データベースに圏論が使い放題

これで、「デイヴィッド・スピヴァックはデータベース界の革命児か -- 関手的データモデル」に挙げておいた次の対応関係をひととおり説明しました。

データベースの概念 圏論の概念
データベースのスキーマ 圏
データベースのテーブル 圏の対象
テーブルのカラム 圏の射
データベースの状態／インスタンス 関手
データ操作 自然変換

スピヴァックは関手的データモデルの特徴を次のように書いています。

a straightforward model of databases under which every theorem about small categories becomes a theorem about databases.


小さい圏に関するすべての定理がそのままデータベースに関する定理となるような、直接的なデータモデル

この言葉の意味するところ／そのインパクトは実に甚大です。データベースに関する諸概念が、極めて直接的に、圏論のなかにスッポリと埋め込まれてしまいます。そうなれば、データベースに関して圏論の道具が（すべてではないにしろ相当に）使えてしまうのです。圏論の枠組みと道具の強烈さをご存知の方なら、身震いするくらいに凄いことだと気付くでしょう。

随伴やモナド／クライスリ構成は既にスピヴァックが利用し始めています。代数トポロジーや代数幾何の方法、なかでもホモトピー的手法が投入されていく可能性は高いでしょう。ジャック・モラヴァ（Jack Morava）は、"Theories of anything"で、スピヴァック理論に対して僕にはサッパリ理解できない示唆を並べています。まったく根拠のない話ではないでしょう。

もう少し現実的／実務的な話をしましょう； 関手的データモデルの手法は関係モデル以外のデータモデルにも適用できます。NoSQLが台頭している時代の潮流にフィットしていると言えます。スピヴァックは、RDFとSPARCLにも興味があるらしく、しばしば例に出しています。Webにデータベース構造（むしろ半構造）を与えることは、Linked Dataなどの動きで再び注目を浴びるかも知れません。

はじめて関手的データモデルを知ったとき僕が驚愕した事情、そしてのめり込んでしまった理由が少しは伝わったでしょうか。

*1:同姓同名で生年月日も同じ人は区別できないとか、結婚して姓が変わると別人扱いになるとか、現実的な問題がある点は注意しておきます。

*2:僕はアンビエント圏と呼んでいます。SetやPartialが使われます。

*3:実装者の立場では、名前空間や名前形式の決定はかなり頭の痛い問題です。

*4:部分写像の圏におけるモノ射とは限らないです。

*5:可換図式は、実は2-セルです。より正確な記述には高次圏を使うべきでしょう。

*6:実務上、主キー 番号などによるIDカラムは必須だというのはそのとおりだと思いますが、それは、この文脈とは別な話です。

*7:これには、潜在的に高次圏の構成法を使います。

*8:fixedは、プログラミング言語のconstやfinalに似たものです。