レンズを説明するための事例として、僕はしばしば“Webのサーバーサイド処理”を挙げます。レンズはHTTPプロトコルの変換プロセッサに相当し、レンズの結合(直列結合)はパイプライン構成に相当します。
プロ関手は、集合の族に圏が両側から作用している代数構造とみなせます。プロ関手の別名として双加群〈bimodule〉がありますが、集合論的双加群〈両側加群〉は集合にモノイドが作用している代数構造です*1。プロ関手と同義の双加群は、集合論的双加群の台集合を台集合族に、モノイドを圏に一般化した構造です。
圏による両側作用を持つ集合族としてのプロ関手は、レンズと同様に、“Webのサーバーサイド処理”を事例として説明できます。プロ関手の左作用/右作用/両側作用と、Web処理アーキテクチャとのアナロジーを追えば、抽象的な概念を身近な実務的具体例を通して理解できます。$`
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\mbf}[1]{ \mathbf{#1} }
\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\o}[1]{ \overline{#1} }
%\newcommand{\id}{ \mathrm{id} }
\newcommand{\In}{ \text{ in }}
%\newcommand{\On}{ \text{ on }}
\newcommand{\op}{ \mathrm{op}}
\newcommand{\hyp}{\text{-} }
\newcommand{\LAct}{\mathop{\triangleright} }
\newcommand{\RAct}{\mathop{\triangleleft} }
`$
内容:
Webのサーバーサイド処理とレンズ
Webのサーバーサイド処理を、2つの部分〈コンポネント〉に分けて考えます。ひとつは、サーバーサイドの出入り口側に位置するコンポネントで、変換プロセッサ〈transform processor〉と呼びましょう。もうひとつは、奥側〈アップストリーム〉に居るピボット・プロセッサ〈pivot processor〉です。この2つのコンポネントを絵に描けば次のようです。
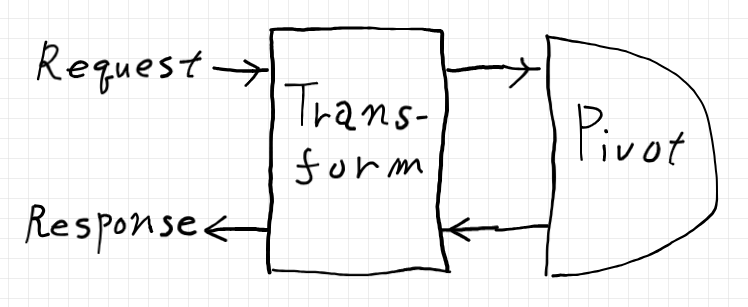
変換プロセッサは双方向データ処理〈bidirectional data-processing〉を行うコンポネントです。変換プロセッサの内部構造は次のようだとします。
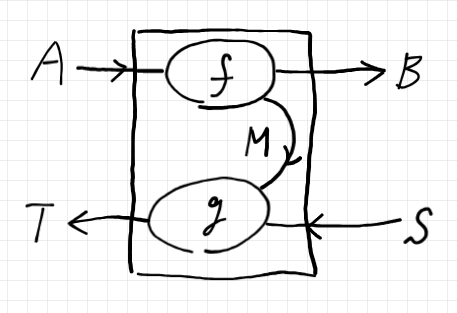
これは、レンズ〈lens〉と呼ばれる構造です。レンズの構成素を、Web処理の文脈で説明すると:
- $`A`$ : 外部からのリクエストのデータ型
- $`B`$ : サーバー内部のリクエスト(ピボット・プロセッサへのリクエスト)のデータ型
- $`f`$ : 外部からのリクエストを内部のリクエストに変換する関数
- $`S`$ : サーバー内部のレスポンス(ピボット・プロセッサからのレスポンス)のデータ型
- $`T`$ : 外部へのレスポンスのデータ型
- $`g`$ : 内部のレスポンス(ピボット・プロセッサからのレスポンス)を外部へのレスポンスに変換する関数
- $`M`$ : 変換プロセッサの内部通信チャンネルに使うデータ型(コンポネント外部には非公開)
変換プロセッサ、つまりレンズを幾つも繋いでパイプラインを構成できます。レンズ達は、リクエスト・データ型とレスポンス・データ型のペア(例えば $`(A, T)`$)を対象とする圏を形成します。圏の射がレンズですが、レンズの向きはリクエストの向きに合わせると約束します。これは単に約束なので、射の向きを逆向きに約束してもかまいません。
レンズの圏〈category of lenses〉において、ピボット・プロセッサは、余域が $`(\mbf{1}, \mbf{1})`$ である射〈レンズ〉として定義できます。ここで、$`\mbf{1}`$ はデカルト圏の単位対象、特に集合圏では特定された単元集合です。
プロ関手
プロ関手〈profunctor〉とは、変性〈variance〉が反変-共変の二項前層です。前層/余前層は余域が集合圏である関手のことなので、プロ関手 $`P`$ は次のように書けます。
$`\quad P : \cat{C}^\op \times \cat{D} \to \mbf{Set} \In \mbf{CAT}`$
多くの場合、圏 $`\cat{C}, \cat{D}`$ は小さいと仮定します(小さくない場合も考えますが)。変性を反変-共変としているのも約束で、違う約束にしても問題ありません。実は、変性はどうとでもなるのです。例えば、
$`\quad Q:\cat{C}\times \cat{D}^\op \to \mbf{Set} \In \mbf{CAT}`$
であったとしても、$`\cat{C'} := \cat{C}^\op`$ 、$`\cat{D'} := \cat{D}^\op`$ と置けば、次の形になります。
$`\quad Q : \cat{C'}^\op \times \cat{D'} \to \mbf{Set} \In \mbf{CAT}`$
なんでもいいので約束を決めれば、“他の約束”を“決めた約束”に適合させること(あるいはその逆)は出来ます。なので、約束の決め方はどうでもいいのですが、異なる約束のあいだの翻訳作業はけっこう大変です。圏論では、異なる約束のあいだの翻訳で消耗する事態はしょっちゅうありますね。鬱陶しい話ですが、約束を統一するのは無理なので致し方ないです*2。
捻じれアロー対
レンズの圏と似てますが、違った構成法による圏を紹介します。レンズの圏は、デカルト圏 $`\cat{C}`$ (より一般には対称モノイド圏)をもとに構成できます。ここで述べる圏は単なる圏〈プレーンな圏〉 $`\cat{C}`$ をもとにして構成できます。圏 $`\cat{C}`$ の捻じれアロー圏〈twisted arrow category〉と呼ばれるものです。
圏 $`\cat{C}, \cat{D}`$ の捻じれアロー対〈twisted arrow pair〉とは、$`\cat{C}^\op \times \cat{D}`$ の射のことです。要は、射の方向が逆になっているペアなので、$`\cat{C} \times \cat{D}^\op`$ の射と定義してもかまいません。これも約束の問題です。「アロー」と「射」は同義ですが、なぜかこの場合は「アロー」を使う習慣です。捻じれアロー対は、単に捻じれアロー〈twisted arrow〉、捻じれ対〈twisted pair | 捻じれペア〉とも呼ばれます。
捻じれアロー対については、以下の過去記事に詳しい説明があります。
捻じれアロー対は、単に直積圏の射に過ぎませんが、レンズやオプティクの最も単純なケースと考えることができます。圏 $`\cat{C}`$ がデカルト圏(より一般には対称モノイド圏)のとき、$`\cat{C}`$ からレンズの圏 $`\mrm{Lens}(\cat{C})`$ を構成できますが、捻じれアロー対を射とする圏 $`\cat{C}^\op\times \cat{C}`$ (あるいは $`\cat{C}\times \cat{C}^\op`$)は $`\mrm{Lens}(\cat{C})`$ に規準的〈canonical〉に埋め込めます。
さて、捻じれアロー対を射とするが、対象が $`\cat{C}`$ の射である圏を考えます。上記の $`\cat{C}^\op\times \cat{C}`$ とは微妙に違います。これから定義する、対象が $`\cat{C}`$ の射で、射が捻じれアロー対である圏を $`\mrm{Tw}(\cat{C})`$ と書き、圏 $`\cat{C}`$ の捻じれアロー圏〈twisted arrow category〉と呼びます。捻じれアロー圏は、$`\cat{C}^\op\times \cat{C}`$ とは別物なので注意してください。
$`f, g\in \mrm{Mor}(\cat{C})`$ から構成される捻じれアロー対を $`(\o{f}, g)`$ と書きます。$`\o{f}`$ は、反対圏 $`\cat{C}^\op`$ の射とみなした $`f`$ です(このオーバーライン記法については、「状態遷移系としての前層・余前層・プロ関手 // 捻じれ対のテキスト表示と図示」参照)。
$`|\mrm{Tw}(\cat{C})| := \mrm{Mor}(\cat{C})`$ です。2つの対象 $`x, y\in |\mrm{Tw}(\cat{C})|`$ に対して、次の状況を考えましょう。
$`\quad (\o{f}, g) : x \to y \In \mrm{Tw}(\cat{C})`$
これは、次のことだと定義します。
$`\quad f: A \to B \In \cat{C}\\
\quad x: B \to S \In \cat{C}\\
\quad g: S \to T \In \cat{C}\\
\quad y = f;x;g \In \cat{C}
`$
$`y`$ を絵で描けば以下のようです。
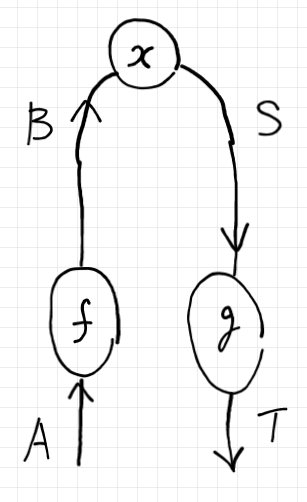
$`\mrm{Tw}(\cat{C})`$ の射は捻じれアロー対なので、射の結合は捻じれアロー対の結合、恒等射は恒等射の対〈ペア〉です。
“曲がった射=ピボット”とグロタンディーク構成
捻じれアロー圏 $`\mrm{Tw}(\cat{C})`$ は、圏 $`\cat{C}`$ から簡単に構成できる圏です。が、興味深い解釈や背景を持ちます。
前節最後の絵から分かるように、圏 $`\mrm{Tw}(\cat{C})`$ の対象は“曲がった射”です。“曲がった”と言っているのは、絵からのイメージであり実際には単に $`\cat{C}`$ の射に過ぎません。が、“曲がった射”だと思うと、心理的納得感は増します。
曲がった射は、先に述べたWeb処理の言葉ではピボット・プロセッサのことです。ピボット・プロセッサは、捻じれアロー対達のパイプラインの旋回エンドポイントを与えます。ピボット・プロセッサを単にピボット〈pivot〉とも略称します。
捻じれアロー圏 $`\mrm{Tw}(\cat{C})`$ は、レンズの圏 $`\mrm{Lens}(\cat{C})`$ のピボットを対象として、内部通信チャンネルを持たない変換プロセッサ(単純なレンズ)を射とする圏です。
また、ピボットに捻じれアロー対を適用する操作は、「ホム関手とサンドイッチ結合」で述べたサイドイッチ結合〈sandwich composition〉になっています。
$`\quad \cat{C}(B, S)\ni x \mapsto f;x;g \in \cat{C}(A, T)`$
さらに、捻じれアロー圏 $`\mrm{Tw}(\cat{C})`$ は、圏 $`\cat{C}`$ のホム双関手 $`\mrm{Hom}_{\cat{C}}`$ のグロタンディーク構成になっています。値を集合圏にとる関手〈前層/余前層〉のグロタンディーク構成は特に要素の圏〈category of elements〉と呼ぶので、ホム双関手 $`\mrm{Hom}_{\cat{C}}`$ の要素の圏が捻じれアロー圏 $`\mrm{Tw}(\cat{C})`$ だ、と言えます。
前段落の事実を確認するには、ホム双関手の定義と、要素の圏の作り方に基づいて、反変-共変の二項前層に対するグロタンディーク構成(の特殊ケース)を忠実に実行してみてください。
プロ関手でもピボットとサンドイッチ結合
圏のホム双関手はプロ関手の特別なものです。逆に言えば、プロ関手はホム双関手を一般化したものです。ホム双関手 $`\mrm{Hom}_{\cat{C}} = \cat{C}(\hyp, \hyp)`$ の値(集合)の要素は射ですが、プロ関手 $`P`$ の値(集合)の要素はなんだか分かりません。なんだか分からない要素なのですが、それを“ピボット=曲がった射”と想定するとプロ関手に対する強いメンタルモデルを持てます。定義や推論に実感が持てるようになります。
ここでは、プロ関手(特に自己プロ関手〈endo-profunctor〉)の値 $`P(B, S)`$ の要素を($`B`$ から $`S`$ への)ピボット〈pivot〉と呼びます。もちろん、この呼び名は前節までの“曲がった射”、“ピボット・プロセッサ”などの具体例を想起するためのものです。実際には、ピボットは単なる集合の要素であり、具体的に何であるかは不明なシロモノです。
今の文脈では、プロ関手(自己プロ関手) $`P: \cat{C}^\op\times \cat{C}\to \mbf{Set}`$ の(対象パートの)値 $`P(B, S)`$ はピボットセット〈pivot-set〉となります -- ピボット達の集合ですから。ホム双関手の場合は、値はホムセット〈homset〉でした -- 準同型射〈homomorphism〉達の集合とみなすからです*3。プロ関手を状態遷移系の一般化と考えるとき(「 状態遷移系としての前層・余前層・プロ関手 」参照)には、ピボットセットではなく状態空間〈state space〉と呼びます。背後にあるメンタルモデルや実例により呼び名が変わっています。が、抽象的・形式的定義は何も変わりません。同じ概念に同義語がたくさんあるだけです。
プロ関手の対象パートがピボットセットの族〈ファミリー〉としてイメージできたら、射パートは、捻じれアロー対によるサンドイッチ結合とみなせます。ピボット $`x\in P(B, S)`$ に対して捻じれアロー対 $`(\o{f}, g)`$ を適用することが、プロ関手 $`P`$ の射パートである両側作用を与えます。
$`\quad P(B, S)\ni x \mapsto f\LAct x \RAct g \in P(A, T)`$
一般的なプロ関手では、サンドイッチ結合がプレ結合とポスト結合で与えられるとは限らないので、左作用演算子 $`\LAct`$ と右作用演算子 $`\RAct`$ を使って両側作用を書いています。
両側作用の片側を恒等射による作用とすると、左作用と右作用が定義できます。左作用はプレ結合引き戻しの一般化、右作用はポスト結合前送りの一般化です。老婆心で注意しておけば、「左と右」も単なる約束です。違った約束をすれば、左作用がポスト結合前送りに相当するかも知れません。左・右や正・余などの形容詞が何を意味するかは毎回チェックが必要です*4。
「米田テンソル計算 1: 経緯と発想」に載せた、以下のような絵は、ピボットとサンドイッチ結合のメンタルモデルが背後にあります。
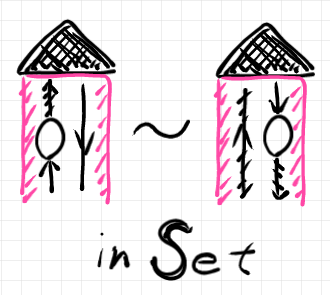
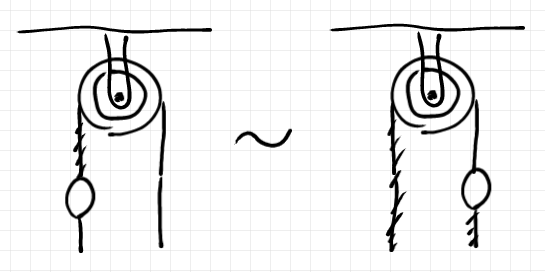
このような絵を見てもピンと来なかったとしたら、ピボットとサンドイッチ結合のメンタルモデルが欠けていたのでしょう。特定のメンタルモデルにこだわり過ぎるのも弊害がありますが、ピボット&サンドイッチ結合は、かなりの場面で有効なメンタルモデルです。