ウィリアム・ローヴェル(William Lawvere)が、「距離空間は豊饒圏(enriched category)なんだよ」と指摘したことは有名な話です。ローヴェルの例において、圏とみなした非負実数で豊饒化された圏は、通常の距離空間を少し拡張したものになっています。今日は、豊饒圏の話は脇に置いといて、結果として得られる“一般化された距離空間”について紹介します。
なお、距離空間と豊饒圏の話は次のエントリーで触れています。
内容:
距離の条件
Xを集合として、その要素を便宜上(あるいは気分の問題で)点と呼ぶことにします。Xの2点の組 (x, y) に非負実数値(無限大∞も入れる) d(x, y) が対応している状況を考えます。d = d(-, -) = λ(x, y)∈X×X.d(x, y) が距離(metric, distance)であるとは、次の条件が満たされることです。
- 任意の3点 x, y, z∈X に対して、d(x, y) + d(y, z) ≧ d(x, z) 。
- 任意の2点 x, y∈X に対して、d(x, y) = d(y, x) 。
- 任意の点 x∈X に対して、d(x, x) = 0 。
- 任意の2点 x, y∈X に対して、d(x, y) = 0 ならば x = y 。
最初の条件は距離の三角不等式で、yを経由して回り道するより、直接 x→z と行ったほうが近い、という内容です。二番目は距離の対称性で、距離は二点のみで決まりその順序によらない、と主張しています。三番目と四番目は、まとめて「d(x, y) = 0 ⇔ x = y」と書けます;「二点間の距離がゼロ ⇔ その二点は同じ点」ということです。
常識的な意味での「距離」は、この条件を満たすことが多いでしょう。
距離の例
意外な量が距離になっていることがあります。Aを有限集合(例えば {a, b, c})として、X = Pow(A) とします。XはAのベキ集合(power set)です。Xの点とは、Aの部分集合です。x∈X のように書きますが、点xと言っても、この例では x⊆A という集合になっています。
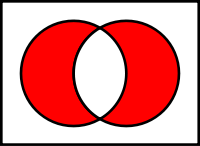
x, y∈X(つまり、x⊆A、y⊆A)に対して、(x\y)∪(y\x) という集合が作れます。ここで、「\」は差集合です。(x\y)∪(y\x) は、集合の対称差と呼ばれるもので、(x∪y)\(x∩y) とも書けます。x△y := (x\y)∪(y\x) = (x∪y)\(x∩y) と略記しましょう。対称差のベン図は次のような感じです(図はWikipedia http://upload.wikimedia.org/wikipedia/commons/thumb/4/46/Venn0110.svg/200px-Venn0110.svg.png から拝借しました)。
さて、
- d(x, y) := (x△y の要素の個数)
と定義します。A ={a, b, c}、X = Pow(A) = {{}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} のケースでいくつかの値を求めてみると:
- d({}, {a, b}) = 2
- d({a}, {a, b}) = 1
- d({a, b}, {a, b}) = 0
- d({b}, {c}) = 2
- d({a}, {a, b, c}) = 2
- d({a, b}, {a, b, c}) = 1
- d({a, b}, {b, c}) = 2
- d({}, {a, b, c}) = 3
このように定義された d(x, y) が、実際に距離の条件を満たしているのを確認するのは良い練習問題です。やってみてください。
いま定義した d(x, y) は、三角不等式 d(x, y) + d(y, z) ≧ d(x, z) より強い、次の条件を満たします。
- max(d(x, y), d(y, z)) ≧ d(x, z)
max(s, t) は、sとtの大きいほう(正確には小さくないほう)です。この条件を満たす距離は超距離(ultrametric)と呼ばれます。超距離は、通常の三角不等式も満たすので距離の特別な種別となっています。
この例は、二進信号空間のハミング距離(Hamming distance)と同じものです。二進信号(ビット列)のハミング距離は、長さがnのビット列xとyに対して、d(x, y) = (xとyで、同じ位置で値が異なるビットの個数) として定義される超距離です。
距離の条件をゆるめる
最初に挙げた距離の条件のなかで、次のものを除外しましょう。
- 任意の2点 x, y∈X に対して、d(x, y) = d(y, x) 。
- 任意の2点 x, y∈X に対して、d(x, y) = 0 ならば x = y 。
残る条件は次の2つだけです。
- 任意の3点 x, y, z∈X に対して、d(x, y) + d(y, z) ≧ d(x, z) 。
- 任意の点 x∈X に対して、d(x, x) = 0 。
d(x, y) を点(位置)xから点yへと移動するときのコストと考えましょう。コストは、燃料とか労力とか費用とかを総称したものです。条件として残した2つの命題の解釈は:
- 任意の3点 x, y, z∈X に対して、x→y→z とyを経由した場合のコストは、x→z と直行した場合のコストより小さくなることはない。
- 任意の点 x∈X に対して、xからxへの移動(何もしない)のコストは0である。
除外した条件について考えてみます。点xから点yへの道が上り坂だとします。d(x, y) は上り坂を登る労力がかかります。d(y, x) は反対に下りなので楽でしょう。この場合、コストとして d(x, y) = d(y, x) は成立しません。
通信ネットワークにおける“距離”を、経由したルーターを勘定して定義することがあります。2つの機器(ノード)が、同じLAN内にあればルーターなしで通信できます。距離はゼロとなります。この例では、d(x, y) = 0 でも、xとyが同じノードとは限りません。
移動のコストと考えた距離では:
- xからyへ行くコストと、yからxへ行くコストが同じとは限らない。
- コストゼロで、異なる点のあいだで移動できることがある。
極端な距離
一般化された(条件をゆるめた)距離でも、距離の値は0以上∞以下の実数値となります。距離の値に制限を付けることがあります: Xが離散的な対象物であるときは、距離は 0, 1, 2, ... のような整数値がふさわしいことも多いでしょう。無限大(∞)を認めないときもあります。適当な有限の値Dを決めて、d(x, y) ≦ D と制限したほうが都合がいいこともあります。
さてここで、距離の値を0か∞のどちらかに制限してみます。距離の条件をゆるめているので、次の点に注意してください。
- d(x, y) = 0 でも x = y とは限らない。
- d(x, y) = 0 でも d(y, x) = 0 とは限らない。
- d(x, y) = ∞ でも d(y, x) = ∞ とは限らない。
値が0か∞である距離dに対して、記号「≦」を次のように定義します。
- x ≦ y とは、d(x, y) = 0 のこと。
すると、次が成立します。
- x ≦ x
- x ≦ y かつ y ≦z ならば、x ≦ z
これは、プレ順序(pre-order)の条件です。「d(x, y) = d(y, x) = 0 ならば x = y」を付け加えると順序になります。
つまり、プレ順序や順序は、極端な(一般化された)距離としても表現できるのです。このへんのことは、最初に述べた豊饒圏による解釈だとスッキリ定式化できますが、とりあえず、事実としてチョット面白いでしょ。