豊饒圏をちゃんと定義したい - 檜山正幸のキマイラ飼育記 (はてなBlog)

僕が豊饒圏の話をするとき、定義を最後まで書き切らないで「他にいくつかの法則を満たす必要があります」みたいな言い方でお茶を濁しています。その理由は、定義を書くだけでもとてもめんどくさいからです。

ちゃんと（若干の省略がありますけどね）記述してみると、どのくらいめんどくさいかやってみました。機械可読な定義の下調べです。あるいは、詳細に拘る人に対する説明。僕自身は全然詳細に拘らないんだけど。

内容：

言葉の問題／記法の約束
モノイド圏
五角形等式と三角形等式
V豊饒圏
感想

言葉の問題／記法の約束

"enriched category"に「豊饒圏」という訳語を使ってますが、「ほうじょう」には「豊饒」と「豊穣」があるんですよね。特に根拠はなく「豊饒」を使ってます。

豊饒圏を定義するには、まずモノイド圏Vを選んで固定します。このVはenriching category（ingに注意）と呼ばれたりします。enriching category Vに対してenriched categoryを考えるわけです。-ingと-edを日本語ではどう表したらいいのでしょう。例えば、-edを「被-」、-ingを「-化」とすると、「豊饒化圏Vに対する被豊饒圏」となります。が、被豊饒圏なんて言葉は誰も使いそうにないのでダメですね。豊饒化圏も紛らわしいので、豊饒化ベース圏とかくどい言い方をしたほうが無難でしょう。

とりあえずここでは、豊饒圏（enriched category）と豊饒化ベース圏（enriching (base) category）を使うことにします。

等式 a = b において、a, bがどんな集合に属するかを明示したいとき次の書き方を採用します。

a = b over A

a =_A b という書き方もありますが、下付きだと見難くなるのでこの記法にしました。overを太字にしているのは、等式の一部のように見えないように、です。

f:A→B が圏Cのなかの射であるとき、次のように書くことがあります。

f:A→B in C （inは太字にしないで使うことが多いです。）

モノイド圏

豊饒圏を定義する土台になる豊饒化ベース圏はモノイド圏である必要があります。対称モノイド圏であることを仮定することも多いですが、豊饒圏を定義するだけなら対称性は要りません。

モノイド圏の定義からしてめんどくさいのですが「ちゃんと定義」の趣旨に沿って記述しておきます。記号の乱用で、モノイド圏を V = (V, $\otimes$ _V, I_V, α^V, λ^V, ρ^V) と書くことにします。

「ちゃんと」とは言っても、記号の乱用をしないとやってられんです。記号Vは二重の意味で使っていて、すぐ上の等式の左辺はモノイド圏全体を表し、右辺に出てくるVは普通の圏で、モノイド構造を載せる台（underlying category）です。「|V|、dom、cod、;、id」などは普通の意味で使います。要するに、台圏に対する普通の圏の構造は既知とします。

$\otimes$ _Vは、V×V→V という双関手（二項関手）です。I_Vは圏Vの特定の対象。α^V, λ^V, ρ^V はV上で定義された自然同型（成分が同型射である自然変換）です。以下、下付き・上付きのVは了解されているものとして省略します。このテの省略もしないと、記号が煩雑になってやってられんです。

双関手 $\otimes$ をVのモノイド積またはテンソル積と呼びます。対象IはVのモノイド単位またはテンソル単位、あるいは単に単位と呼びます。α, λ, ρは、モノイド積の結合律、左単位律、右単位律がup-to-isoで成立することを述べるときのiso達ですが、呼び名はなんか色々あるようです。各法則の構造同型射（structure/structural isomorphism）と呼んでおけばたいてい通じるでしょう。αならば、結合律の構造同型射と言えばいいのです*1。V = (V, $\otimes$ , I, α, λ, ρ) がモノイド圏であるためには、いくつかの法則（公理）を満たすことを要求します。

まずは、 $\otimes$ が双関手であることを書き下します。f:A→B, g:B→C, f':A'→B', g':B'→C' だとして、

(f;g) $\otimes$ (f';g') = (f $\otimes$ f');(g $\otimes$ g') over V(A $\otimes$ A', C $\otimes$ C')
id_A $\otimes$ id_B = id_AB over V(A $\otimes$ B, A $\otimes$ B)

T(A, A') = A $\otimes$ A'、T(f, f') = f $\otimes$ f' のように書いてみると、上の条件が T:V×V→V が関手であることに対応しているのが分かるでしょう。 $\otimes$ の双関手性は、通常交替律（interchange law）と呼ばれます。交替律がけっこう日常的なことは次にエントリーに書いています。

次にα、λ、ρの話です。α、λ、ρは自然変換です。自然変換は関手から関手への変換なので、どんな関手のあいだで変換をしてるかをハッキリさせましょう。ラムダ式で関手を表しますが、λが自然変換のひとつなので、ラムダ抽象に大文字Λを使います。対象に関する対応しか書きませんが、射も同様です（って言い方はあまり「ちゃんと」してない）。

A1 = Λ(A, B, C).(A $\otimes$ B) $\otimes$ C :V×V×V→V
A2 = Λ(A, B, C).A $\otimes$ (B $\otimes$ C) :V×V×V→V
L1 = Λ(A).I $\otimes$ A :V→V
L2 = Λ(A).A :V→V
R1 = Λ(A).A $\otimes$ I :V→V
R2 = Λ(A).A :V→V

自然変換α、λ、ρのプロファイルは次のようです*2。これは、自然変換::関手1⇒関手2:圏1→圏2 という書式です。

α::A1⇒A2:V×V×V→V
λ::L1⇒L2:V→V
ρ::R1⇒R2:V→V

α、λ、ρ を成分表示で露骨に書けば：

α_A,B,C:(A $\otimes$ B) $\otimes$ C→A $\otimes$ (B $\otimes$ C)
λ_A:I $\otimes$ A→A
ρ_A:A $\otimes$ I→A

α、λ、ρの成分であるα_A,B,C、λ_A、ρ_AはすべてV内の同型射です。したがって、α_A,B,C^-1、λ_A^-1、ρ_A^-1 が存在します。

ちゃんと定義するなら、α、λ、ρの自然性と同形性（可逆性）の等式を全部書き下す必要があるでしょう。あー、めんどくさい。でも、自然性の等式は書いておきます。f:A→A'、g:B→B'、h:C→C' として、

α_A,B,C;(f $\otimes$ (g $\otimes$ h)) = ((f $\otimes$ g) $\otimes$ h);α_A',B',C' over V((A $\otimes$ B) $\otimes$ C, A' $\otimes$ (B' $\otimes$ C))
λ_A;f = (id_I $\otimes$ f);λ_A' over V(I $\otimes$ A, A')
ρ_A;f = (f $\otimes$ id_I);ρ_A' over V(A $\otimes$ I, A')

さて、自然同型α、λ、ρはさらに別な法則を満たすことを要求します。五角形等式と三角形等式です。

五角形等式と三角形等式

五角形の話と絵は「2月の圏論勉強会」（2009年）と「マックレーンの五角形の絵」（2011年）に書いてあります。以下にまた新しく描いた五角形の絵。

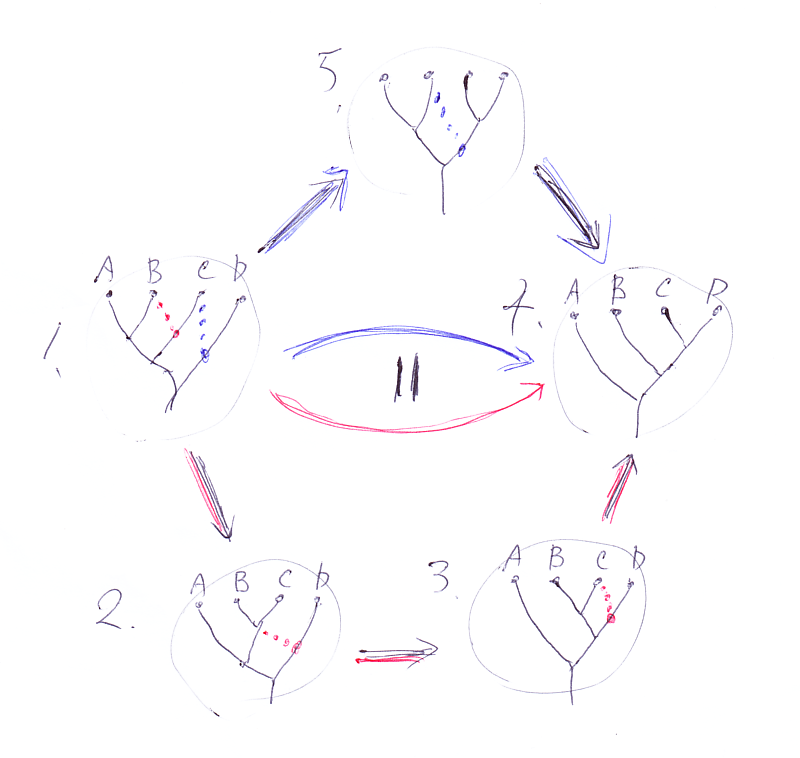
この五角形の絵を見ながら、左の頂点（番号は1）から右の頂点（番号は4）に下側を通って行く経路を書き下します。

1→2 は、α_A,B,C $\otimes$ id_D
2→3 は、α_A,BC,D
3→4 は、id_A $\otimes$ α_B,C,D

これらを結合してまとめると、(α_A,B,C $\otimes$ id_D);α_A,BC,D;(id_A $\otimes$ α_B,C,D)。

上側を通って行く経路のほうは、

1→5 は、α_AB,C,D
5→4 は、α_A,B,CD

まとめると、α_AB,C,D;α_A,B,CD。

五角形が可換図式なら上下の経路が等しいので、次の等式になります。

(α_A,B,C $\otimes$ id_D);α_A,BC,D;(id_A $\otimes$ α_B,C,D) = α_AB,C,D;α_A,B,CD over V(((A $\otimes$ B) $\otimes$ C) $\otimes$ D, A $\otimes$ (B $\otimes$ (C $\otimes$ D)))

三角形等式は、次の三角形が可換であることを主張します。

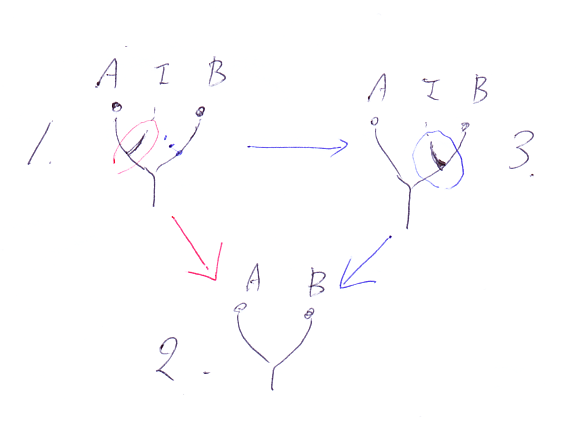
[追記 date="翌日"]以下、間違ってました。取り消し線の下に訂正。[/追記]

対応する等式は：

~~ρ_A $\otimes$ id_B = id_A;α_A,I,B;λ_B over V((A $\otimes$ I) $\otimes$ B, A $\otimes$ B)~~
ρ_A $\otimes$ id_B = α_A,I,B;(id_A $\otimes$ λ_B) over V((A $\otimes$ I) $\otimes$ B, A $\otimes$ B)

V豊饒圏

豊饒圏の話題は次のエントリーで扱っています。これらのエントリーのテーマは内部ホムと自己豊饒化です。豊饒圏の定義はちゃんとしてませんが、実例は挙げています。

上記エントリーに「豊饒圏としての距離空間」の例もありますが、より詳しくは「可愛い圏」の「可愛い豊饒圏」と「移動のコストとしての距離」に書いてあります。距離空間や順序集合を豊饒圏とみなすのは、ちょっと楽しいですし、定義の確認にはうってつけです。

さて、豊饒圏のちゃんとした定義ですが、モノイド圏Vを固定した上で豊饒圏をK、Hなどで表すことにします。豊饒圏を K = (X, K, γ^K, ι^K) のように書きます。これも記号の乱用で、左辺のKが豊饒圏全体、右辺のKは豊饒圏の構造の一部です。(X, K, γ^K, ι^K) は次のようなものです。

Xは、集合である。
Kは、X×X→|V| という写像である。
γ^Kは、X×X×X→Mor(V) という写像である。（Mor(V) は圏Vの射の集合）
ι^Kは、X→Mor(V) という写像である。

Xは豊饒圏の対象の集合です。以下、X = |K| と書きます。a, b∈|K| に対して、K(a, b)はVの対象で、ホム対象と呼びます。γ^K(a, b, c)、ι^K(a) の代わりに下付き添字記法 γ^K_a,b,c、ι^K_a を使い、上付きのKは省略することにします。記号の乱用と省略の結果、K = (|K|, K, γ, ι) と短く書けます。

(|K|, K, γ, ι)がV豊饒圏であるためには、まず次の条件が必要です。

dom(γ_a,b,c) = K(a, b) $\otimes$ K(b, c)
cod(γ_a,b,c) = K(a, c)
dom(ι_a) = I
cod(ι_a) = K(a, a)

別な書き方をすると：

γ_a,b,c:K(a, b) $\otimes$ K(b, c)→K(a, c) in V
ι_a:I→K(a, a) in V

γは射の結合演算を与え、ιは対象の恒等射を与えます。なので、射の結合（composition）の結合律（associative/associativity law）と恒等の左右の単位律が要求されます。

結合律を書き下すために、最初は K(a, b) などを写像の集合だと思ってみましょう。f∈K(a, b)、g∈K(b, c)、h∈K(c, d) として、(f;g);h = f;(g;h) の中置演算子記号「;」を前置のγに直せば次のように書けます。

γ(γ(f, g), h) = γ(f, γ(g, h))

この状況は、次の絵で表現できます。この絵を見ながら考えると分かりやすいです。

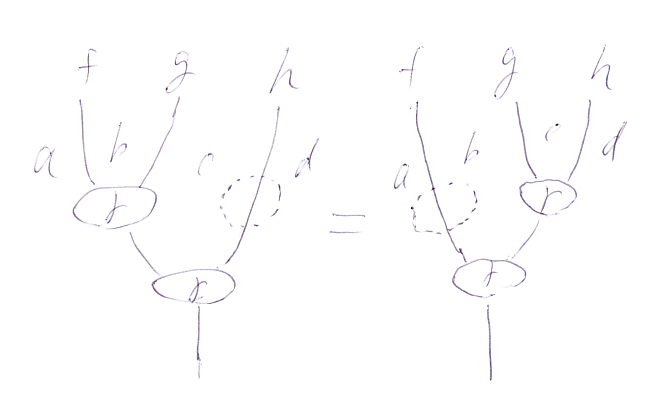
図で点線で描かれた丸は恒等に対応します。これを考慮すると、h = id(h)、f = id(f) なので、

γ(γ(f, g), id(h)) = γ(id(f), γ(g, h))

写像の直積を×で表すと（(f×g)(x, y) = (f(x), g(y))）、

γ(γ×id)((f, g), h) = γ(id×γ)(f, (g, h))

写像の結合（合成）を図式順の演算子「;」で書けば、

(γ×id);γ = (id×γ);γ

厳密には、((f, g), h) → (f, (g, h)) というトリプルの変換である自然同型αが働いているので、

(γ×id);γ = α;(id×γ);γ

下付き添字をちゃんと付けると次のようになります。

(γ_a,b,c×id_{K(c, d)});γ_a,c,d = α_{K(a, b),K(b, c),K(c, d)};(id_{K(a, b)}×γ_b,c,d);γ_a,b,d

この形になってしまえば、最初に導入したf, g, hはもう出てこないので、集合と写像の解釈から離れて、モノイド圏Vのなかの等式として意味を持ちます。

(γ_a,b,c $\otimes$ id_{K(c, d)});γ_a,c,d = α_{K(a, b),K(b, c),K(c, d)};(id_{K(a, b)} $\otimes$ γ_b,c,d);γ_a,b,d over V(K(a, b) $\otimes$ K(b, c) $\otimes$ K(c, d), K(a, d))

これが、射の結合律の表現になります。ただし、普通はαの作用は省略して次のように書きます。

(γ_a,b,c $\otimes$ id_{K(c, d)});γ_a,c,d = (id_{K(a, b)} $\otimes$ γ_b,c,d);γ_a,b,d over V(K(a, b) $\otimes$ K(b, c) $\otimes$ K(c, d), K(a, d))

同様にして、恒等射の左単位律と右単位律を書き下します。左単位律に対応する絵は次にようになります。右単位律の場合も同様です。

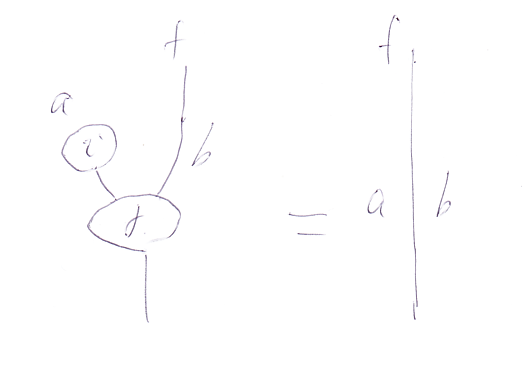
λとρの作用を省略した形なら次のようになります。

(ι_a $\otimes$ id_{K(a, b)});γ_a,a,b = id_{K(a, b)} over V(K(a, b), K(a, b))
(id_{K(a, b)} $\otimes$ ι_b);γ_a,b,b = id_{K(a, b)} over V(K(a, b), K(a, b))