極限(limit)は、圏論でよく使われる構成法です。直積や終対象も極限の一種です。極限の双対は余極限で、これは矢印の向きを反対にした議論をすればいいですね。ここでは、極限を関手の表現対象により説明してみます。
内容:
極限と錐の圏
Cは圏、Dは小さな圏だとして、関手 F:D→C の極限とは、圏Cの対象Lと、X∈|D| ごとの射 πX:L→F(X) の集まりを組にした (L, (πX:L→F(X); X∈|D|)) であって、“ある条件”を満たすものです。“ある条件”をハッキリと述べるためには、関手に対する「錐の圏」を考えるのが良いと思います。
関手 F:D→C の錐(cone)と、次の構成要素からなります。
- Cの対象A
- Dの対象Xごとに、πX:A→F(X) in C
そして、次を満たすとします。
- 任意の射 f:X→Y in D に対して、πX;F(f) = πY
対象Aは錐の頂点(apex)です。関手F、あるいは関手Fによる像部分圏F(D)は錐の底面(base)です。πX:A→F(X) は、頂点Aから底面上の一点F(X)に落ちる母線*1となります。
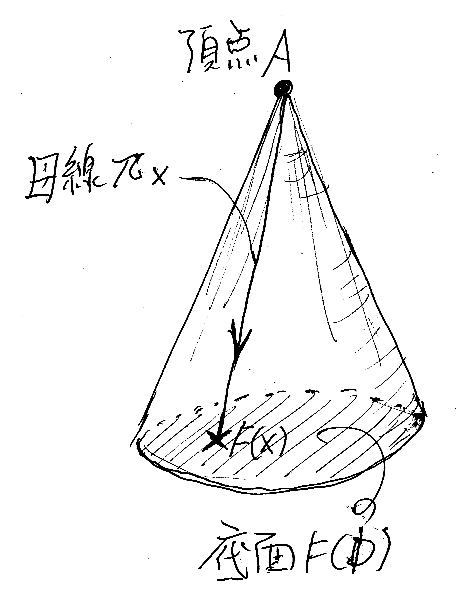
先の等式 πX:A→F(X) πX;F(f) = πY は、頂点Aと底面の二点 F(X), F(Y) が作る三角形が可換図式となることを要求しています。
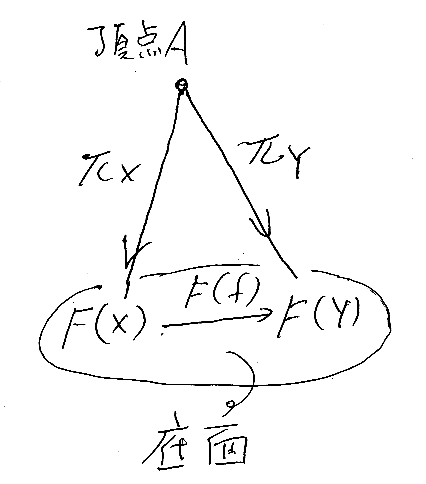
(A, π) と (B, ρ) を、関手 F:D→C に対する錐とします。f:A→B in C が次の条件を満たすとき、fは錐(A, π)から錐(B, ρ)への準同型だと定義します。
- 任意の X∈|D| に対して、f;ρX = πX
関手F:D→Cの錐の全体を対象として、錐のあいだの準同型を射とする圏が構成できます。この圏をFの錐の圏と呼び Cone(F:D→C)、あるいは単に Cone(F) と書くことにします。関手の錐の圏が構成できてしまえば、極限の定義は簡単です。
- 関手Fの錐の圏 Cone(F:D→C) に終対象があれば、それをFの極限と呼ぶ。
極限の例
小さな圏Dとして、二元集合 {1, 2} を離散圏とみなした圏を取ります。関手 F:D→C は、F(1) と F(2) で決まります。F(1) = X1、F(2) = X2 とします。Aを頂点とする錐は (A, π1:A→X1, π2:A→X2) という三つ組です。
錐 (A, π1:A→X1, π2:A→X2) が、錐の圏の終対象であるとは、任意の錐 (B, ρ1:B→X1, ρ2:B→X2) に対して、一意的に f:B→A が決まることです。このfは錐の圏の射ですから、次を満たします。
- f;π1 = ρ1
- f;π2 = ρ2
別な言い方をすると、ρ1:B→X1 と ρ2:B→X2 があると、上の可換性を満たすような f:B→A が一意的に存在します。直積の定義を思い出してもらうと、A = X1×X2 であり、π1とπ2 は直積の射影となります。
次に、小さな圏Dとして単元集合 {1} を離散圏とみなした圏を取ります。すると、関手 F:D→C は、F(1) だけで決まります。F(1) = X とします。Aを頂点とする錐は (A, π:A→X)、つまり、AからXへの射に過ぎません。
この場合の錐の圏は、Xを固定して、A→X というCの射が対象で、可換性を満たす f:B→A が射となる圏です。この定義は、対象X上のオーバー圏に他なりません。関手 F:{1}→C の錐の圏は、C/F(1) と書けるわけです。オーバー圏 C/X の終対象は idX:X→X なので、関手 F:{1}→C の極限は F(1) (とその恒等射の組)となります。
対象も射もまったく持たない圏として空圏を考えることができます。これは、圏とみなした空集合です。0 を空圏として、関手 F:0→C が唯一つ存在します。この関手Fの極限はなんでしょう? まず、錐の圏を考えるのですが、錐の底面は空なので、頂点だけからなる図形がFの錐です。頂点だけとは、Cの対象のことであり、錐のあいだの射もCの対象のあいだの射となります。つまり、空圏からの関手の錐の圏はCそのものです。したがって、関手Fの極限とは、Cの終対象です。
頂点を固定した錐集合
F:D→C を関手として、Cone(F) = Cone(F:D→C) をFの錐の圏とします。Cの対象Aを固定して、Aを頂点とするFの錐の全体を Cone(F)[A] と書くことにします。定義から、Cone(F)[A] は |Cone(F)| の部分集合です(i.e. Cone(F)[A] ⊆ |Cone(F)|)。Dは小さな圏と仮定しているので、錐の底面は小さく、集合 Cone(F)[A] も小さな集合となります。ただし、集合 Cone(F)[A] がどんなものかは一般的にはなんとも言えません。空集合になることもあります。頂点と底面が固定されていても、母線の選び方に多様性があれば、それなりのサイズの集合になることもあるでしょう。
A∈|C| に対して、G(A) := Cone(F)[A] と定義しましょう。G(A) は(小さな)集合ですから、G(A)∈|Set| です。対応 A|→G(A) をC上の反変関手とすることができます。f:A→B in C に対して、Bを頂点とする錐に、fを前結合(pre-compose)すると、Aを頂点とする錐が得られます。これを G(f): G(B)→G(A) とすればよいのです。
以上の手順で定義した関手 G:C→Set はFから決まるので、G = F∧ と書きましょう。上付きの'∧'は錐の形を象徴してます。F∧は、Cの対象に、その対象を頂点とするFの錐集合を対応させる関手です。
- F∧(A) := Cone(F)[A]
- F∧(f:A→B) := f*:Cone(F)[B]→Cone(F)[A]
関手の表現対象
ここらへんから、ちょっと急ぎ足になります。杓子定規の定義を復唱します。
一般に、圏Cから集合圏Setへの反変関手 F:C→Set があるとき、Cの対象Rがあって、任意の対象Aに対して F(A) と C(A, R) が集合として同型となるとき、対象Rは反変関手Fを表現するといいます。また、RはFの表現対象(representing object)と呼びます。
もう少し正確に言うと、ホムセットから作られる C(-, R) という反変関手を考えて、反変関手の圏 [Cop, Set] のなかで、FとC(-, R)が、関手として同型(自然同型)であるとき、対象Rと自然同型変換(成分がすべて同型である自然変換)の組がFの表現となります*2。
いつでも関手の表現対象が存在するわけではありませんが、存在するならup-to-isoの意味で一意的です。表現対象(と対応する自然同型変換)を持つ関手は表現可能(representable)といいます。
集合のベキ集合を作り、逆像対応を考えた反変関手 Pow:Set→Set は、Pow(A) と Set(A, 2) が同型となるので、二元集合2が反変ベキ集合関手Powの表現対象となります。
余談ですが、関手の表現対象は、豊饒圏の文脈でも使えます。例えば、スカラー体K上のベクトル空間の圏VectKは、自分自身で豊饒化されています(ホムセットがベクトル空間となる)。双対空間/双対写像を取る反変関手 D:VectK→VectK は、スカラー体Kで表現されます。
極限対象は、錐集合関手を表現する
いよいよ結論ですが、さらに急ぎ足になります。
関手 F:D→C に対して、次のようにして、集合圏への反変関手 F∧:C→Set が定義されるのでした。
- F∧(A) := Cone(F)[A]
- F∧(f:A→B) := f*:Cone(F)[B]→Cone(F)[A]
F∧は、頂点となる対象に対して、錐の集合を対応させる関手です。
集合圏への反変関手F∧は表現可能な関手です。F∧を表現する対象は、関手Fの極限Lです。より正確に言えば、Fの極限である錐の頂点がLですから、「Fの極限対象がF∧の表現対象だ」となります。
これは、Cの任意の対象Aに対して F∧(A) と C(A, L) が同型であることを意味します。自然同型を与える自然変換をθとすると、Aごとに集合の双射 θA:F∧(A)→C(A, L) を与えて、それが自然変換であることを示すことになります。
練習問題とします(苦笑)、確認してみてください*3。
*1:[追記]母線は、成分線〈component {segment | arrow | line}〉に変更しました。「圏論の極限を具体的に // 関手の極限の復習」参照。[/追記]
*2:C(-, R) は対象Rの米田埋め込みです。反変関手(=前層)Fが表現可能なら、それは“ほぼ”米田埋め込みの像圏に入っています。
*3:自明な練習問題ではありません。