ここ2,3日、カン拡張(Kan extension)を理解しようとジタバタしてました。どうにもイメージがつかめなくて四苦八苦。ワッカラーン。やっとこさで絵に描くことができました。フーッ。
絵を描く前に記号法を: [C, D]は関手圏を表します。圏[C, D]の対象は、C→D という関手、射は関手のあいだの自然変換です。[C, D]は、[C→D]とも書くことにします。矢印の向きを逆にした [D←C]もまったく同じ意味だとします。関手 H:C→D と K:D→E の結合は H;K と書きます。これは図式順です。反図式順のときは、K・H と書くことにします。
さて、問題の右カン拡張(right Kan extension)ですが、J:C→D、G:C→E という状況で、Jに沿ったGの右カン拡張(right Kan extension of G along J)を、JG または GJ と書きます。要するに指数の書き方です。絵とあわせる都合で、図式順のときは JG を、反図式順のときは GJ を採用します。
右カン拡張の基本的性質として、次のカン対応(Kan bijection)があります
- [C, E](J;F, G) = [D, E](F, JG)
イコールは同型です。この同型は、自然変換の集合のあいだの1:1対応を与えます。反図式順で書くなら:
- [E←C](F・J, G) = [E←D](F, GJ)
これは、ラムダ計算のカリー化/反カリー化による同型を連想させます。どうやら、「;」(または「・」)を非対称なモノイド積(テンソル積)と考えて、Jによる掛け算 J;(-) の右随伴である指数 J(-) が右カン拡張となっているようです。
[D, E](JG, JG) = [C, E](J;JG, G) というカン対応が作れるので、左辺にある恒等自然変換の右辺での対応物を run::J;JG⇒G とします。runは自然変換ですが、ある種の実行エンジンで、ラムダ計算のeval(apply)とよく似た働きをします。
以上の状況を描いたのが次の絵です。
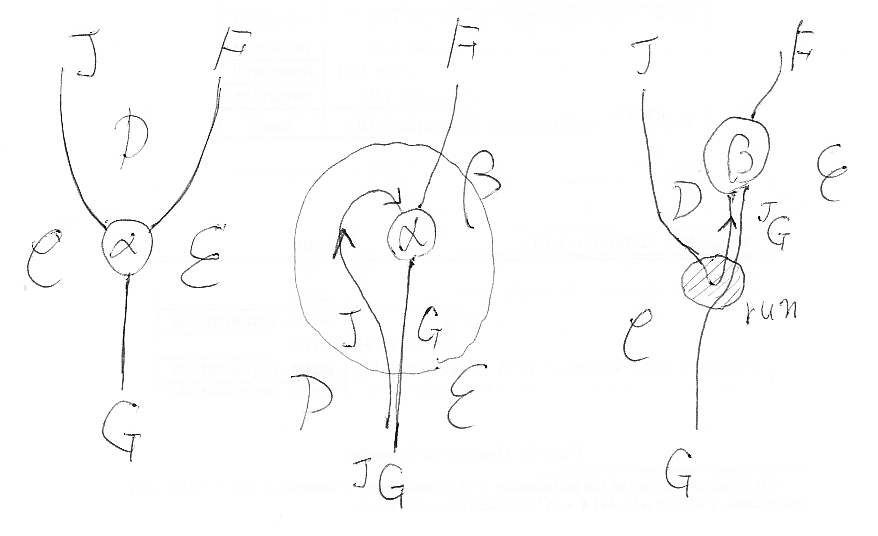
自然変換 α::J;F⇒G をカリー化したものが β::F⇒JG です。指数の肩に乗っているJは、図では逆方向に走るワイヤーで描いています。run::J;JG⇒G を使うと、ワイヤーJのストレッチングによりβのなかに包み込まれているαを引っ張りだすことが出来て、左の絵のαが再現します。
βはαのラムダ抽象と考えることができるので、β = Λα (大文字ラムダを使いました)と書いてもいいでしょう。runの中置記法を仮に >> とすると、J>>Λα = α が成立することになります。ここらへんは、通常のラムダ計算のデカルト閉圏における意味論と同様です。
どうも、右カン拡張は、自然変換のラムダ計算における指数型を与える仕掛けのようです。