このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

心残り：自然変換の大事なこと

雑記／備忘

見出しの「心残り」という接頭辞については「滞っているブログ」とかコメント欄とかを参照。内容は自然変換の話です。

[追記]
コメント欄に、

心残りは色々あるので、続けてもうひとつ記事を書いてみようかな。

と書いてありますが、これは思い立って書いた記事ではありません。

「滞っているブログ」：

僕はブログの下書きをテキストファイルに書くのですが、公開してないで書きかけのドラフト・エントリーが相当数溜まっています。これから書きたいこと、まだまとまってないこと、過去の記事への補足・追加などはたくさんあります。手書きのメモや絵なんかも残っていたりします。

溜まっていたドラフトで、完成に近いものを選んで仕上げたものです。あんまり仕上がってないけど。

[/追記]

自然変換の定義

FとF'は C→D という関手だとします。αがFからF'への自然変換だということを、α::F⇒F':C→D と書くことにします。

自然変換αの実体は、|C|（圏Cの対象の集合）で添字付けられたDの射の族（indexed family of morphisms）です。α = {αX∈Mor(D) | X∈|C| } と書いてもいいかもしれません。ここで、Mor(D) は圏Dの射の全体のことです。

自然変換αは、単なる射の族ってだけではなくて、次に述べる条件を満たす必要があります。

  • 任意の射 f:A→B in C に対して次の図式がD内で可換になる。

F(A)―αA→F'(A)

｜　　　　　　｜

F(f)　　　　　F'(f)

↓　　　　　　↓

F(B)―αB→F'(B)

図の可換性を等式で書き表せば、

  • F(f);αB = αA;F'(f)

となります。この等式は、自然変換の定義ですから、当然に非常に重要です。

自然変換の感じ

圏を点（ドット）、関手を矢印（アロー）で表すと、自然変換は、矢印を結ぶ膜のようなものだと思えます。下の図では、圏が0次元、関手が1次元の図形であり、自然変換は2次元の図形のように描くわけです。自然変換の形状は、二辺形、または二角形です。頂点がCとD、二辺がFとF'、面がαですね。

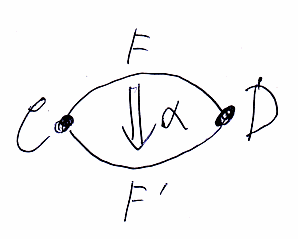
ドットとアローの図のポアンカレ双対を取ると、ストリング図となります。ストリング図では、圏が2次元（面）、関手が1次元（線）、自然変換が0次元（点）となります。習慣として、自然変換は大きさを持たない点ではなくてボックスやオダンゴで表されることが多いです。

下の図の左側は上と同じドット＆アロー、右側が対応するストリング図（オダンゴ図）です。

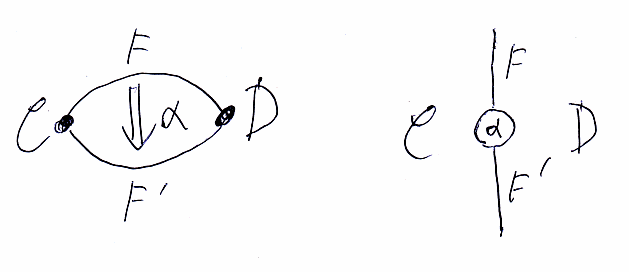
ドット＆アロー図とストリング図のポアンカレ双対については、ウィラートン（Simon Willerton）がきれいな絵を描いているので、それを引用します。ウィラートンは「右から左」「下から上」という方向で図示する人です（「絵算（ストリング図）における池袋駅問題の真相」参照）。

ストリング図はものすごく有用です。特に、キュリアなどが使っている「射と自然変換を混ぜて描く図」は、圏に関する計算を劇的に単純化します。「対象と射を関手と自然変換に格上げする方法」参照。

自然変換を捉えるもうひとつの方法は、自然変換を関手のあいだのホモトピーだとみなすことです。圏を「点（対象）と矢印（射）から出来上がった空間」と考えて、関手は「点を点、矢印を矢印に移す写像」とみなします。すると、自然変換αは関手Fを関手F'へと変形するホモトピーだとみなせます。点Xにおける変形の軌道がαXで与えられます。自然変換αは、そういう軌道の束なので、物体の連続的変形のような“感じ”になります。

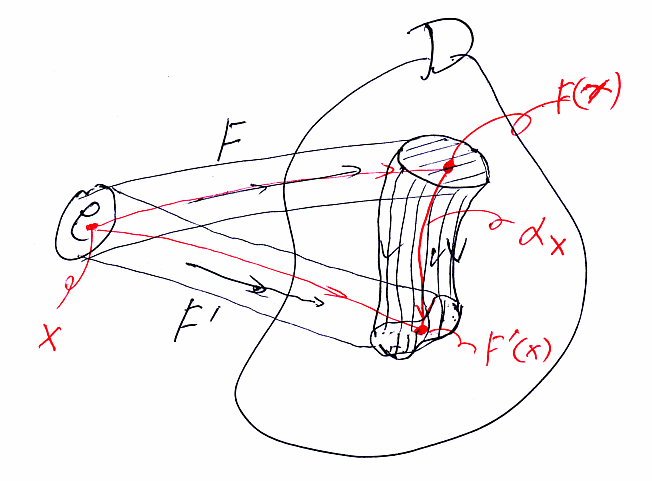
横結合を支える基本等式

α::F⇒F':C→D が自然変換で、もうひとつβという自然変換があるとします； β::G⇒G':D→E 。以下では、関手FとGの反図式順結合を単なる併置で表します。つまり、F;G = GF と書きます。GF(A) = (GF)(A) = G(F(A)) です。

αのA成分 αA:F(A)→F'(A) はDの射なので、これを自然変換 β::G⇒G' によってEに運ぶことができます。βは、G(αA):GF(A)→G'F(A) と G'(αA):G'F(A)→G'F'(A) を結ぶことになります。チーズケーキのような図を描くと分かりやすいでしょう。奥の縦矢印が αA:F(A)→F(A') です。βが自然変換なので、手前の四角形の面が圏E内の可換図式になっています。

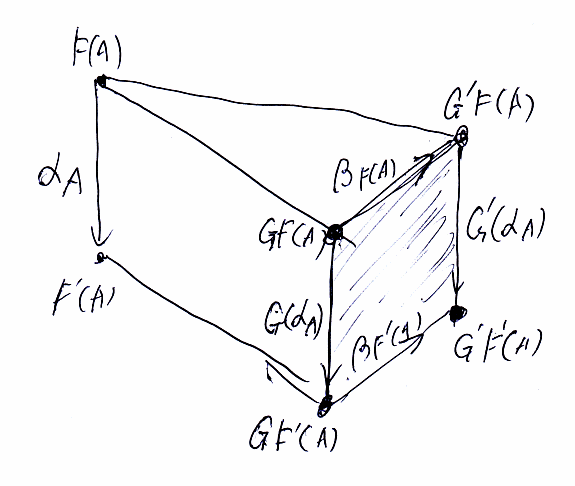
可換性を等式で書き下すと：

  • G(αA);βF'(A) = βF(A); G'(αA)

これはホントに重要な等式です。

上記の等式は、自然変換の横結合（horizontal composition）の定義を合理化します。自然変換αとβの横結合は以下の図のように定義されるのですが、この図とは別な定義をしても同値であることを保証するのが上の等式です。

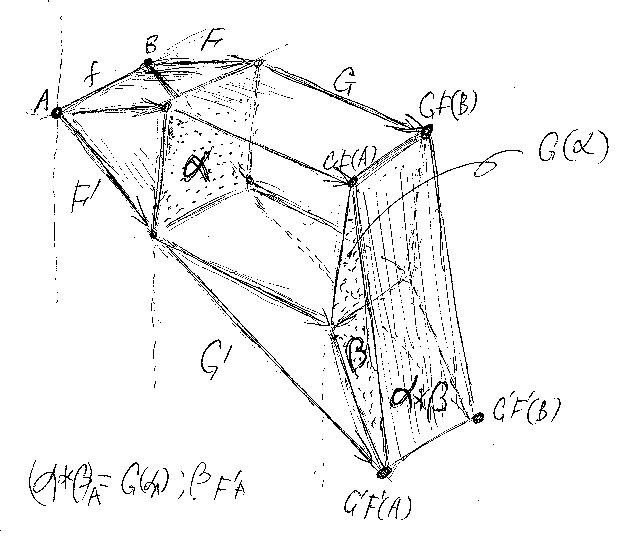
この記事に登場した2つの等式

  1. F(f);αB = αA;F'(f)
  2. G(α);βF'(A) = βF(A); G'(αA)

は、ストリング図のよる関手と自然変換の計算の基盤を与えるものです。絵に描くと、これらの等式が交替律（interchange law）の一種であることが分かります。

そういったことは、「自然変換の計算法 DOTN二号」とそこからリンクされているエントリーに（おおざっぱに）書いてあります。もっとちゃんと書けてないことは、とても心残りです。