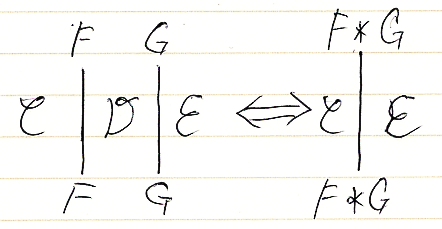[追記 date="後日"]日本語の表記として「抑える」より「押さえる」が正しい気がしてきたけど、このままにします。使い分けがさほど明確なわけじゃないし、「抑える」に「支配下に置く」ような雰囲気もあるので。[/追記]
「圏論の随伴をちゃんと抑えよう」のなかで、絵を使った計算について言及しています。
単位/余単位とニョロニョロ関係式を絵(ストリング図)で描けば次のようです。
これらの公式は、絵(ストリング図)を使うと自然に解釈できますが、その話は次の機会にします。
絵(ストリング図)で計算すれば楽です。絵算(pictorial/graphical/diagrammatic calculation)の話はいずれまとめてする予定です(今日はしない)。
絵が描けるので、随伴系の計算は絵算(pictorial/graphical/diagrammatic calculation)に持ち込めます。
ニョロニョロからホムセット同型の構成は絵算を使えばほぼ自明です。
なんか仄〈ほの〉めかしているだけで実際のところを書いてないのが感じ悪いので、具体的な描画法・計算法を書きます(描きます)。今までで一番詳しい絵算の解説です。
[追記]絵算をやってみたい人は、知識の習得だけでなく、双対や随伴に強くなるためのトレーニングを必ずしましょう。[/追記]
内容:
圏の圏における絵算
絵算に関しては、過去にだいぶ書いているのですが、この記事をだいたいセルフコンテインドにするためにゼロから説明します。今日の絵算の舞台は圏の圏です(他に、モノイド圏における絵算や高次圏における絵算もあります)。
圏の圏における圏論的実体〈categorical entities〉は、圏、関手、自然変換です。それぞれ、0次元、1次元、2次元の実体ですが、絵(ストリング図)にするときはポアンカレ双対にするので、2次元, 1次元, 0次元の図形になります。
| 圏論的実体 | 次元 | 図形 | 図形の次元 |
|---|---|---|---|
| 圏 | 0 | 面 | 2 |
| 関手 | 1 | 線 | 1 |
| 自然変換 | 2 | 点 | 0 |
圏論的演算は、関手の結合〈composition〉、自然変換の縦結合〈vertical composition〉と横結合〈horizontal composition〉の三種類です。関手の結合も横結合と考えれば、縦と横の二種類ともいえます。
1. 圏と関手 F:C→D
関手は縦線(ワイヤー)で描きます。線の方向は上から下ですが、特に必要がないなら矢印は描きません。関手の域は左の面、関手の余域は右の面です。
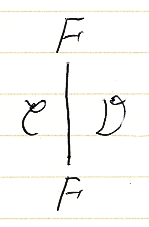
2. 自然変換 α::F⇒G:C→D
自然変換を表す図形は点(0次元)ですが、オダンゴにして内部に名前(ラベル)を書き込みます。
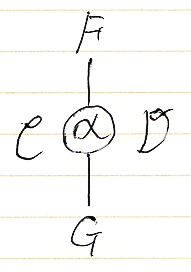
事例
次の絵を考えます。
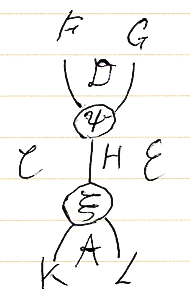
この絵は、次の情報を持ちます。
- F:C→D
- G:D→E
- H:C→E
- K:C→A
- L:A→E
- ψ:F*G⇒H:C→E
- ξ:H⇒K*L:C→E
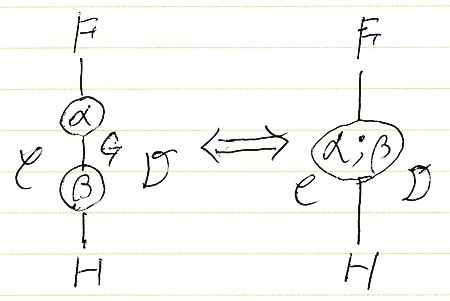
縦結合/横結合を実行した結果をラベルで表現すれば、次の絵になります。
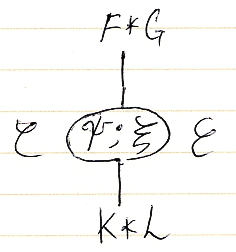
これは、テキスト表記 (ψ;ξ)::F*G⇒K*L:C→E と同じ情報を持ちます。
6. 恒等関手
恒等関手 IdC:C→C は、Cでラベルされた面内に点線で表します。点線なら恒等関手という約束なので、通常はラベルを書きません。右側の絵の赤字は注釈としてC^と書いています。C^はIdCと同じ意味です。必要があれば、右のように恒等関手を明示的に実線で描いてもかまいません。
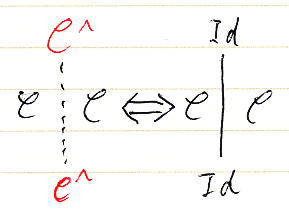
7. 恒等自然変換
恒等自然変換 IDF::F⇒F:C→D *1は、Fのワイヤー(線)上に描いた点線のマルで表します。点線のマルは恒等自然変換という約束なので、通常はラベルを書きません。左側の絵の赤字は注釈としてF^と書いています。F^はIDFと同じ意味です。必要があれば、右側のように恒等自然変換を明示的にオダンゴで描いてもかまいません。
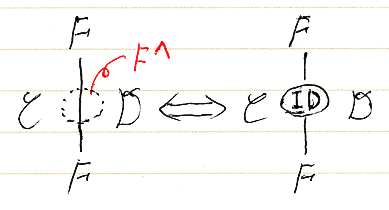
対象と射の格上げ
前節では、圏、関手、自然変換の描き方を示しました。圏の内部には対象と射があります。このままでは、対象と射を描く術〈すべ〉がありません。そこで、格上げ〈bump-up | promotion〉という手法を使います。格上げでは、対象を関手に、射を自然変換に対応させます。
Iを単一の対象と恒等射だけからなる自明圏とします。
- |I| = {0}
- I(0, 0) = {id0}
圏Cの対象Aに対して、Iからの関手A~を次のように定義します。
- A~(0) = A
- A~(id0) = idA
この関手 A~:I→C を対象Aの代わりに使います。絵を描くときは、A~とAを同一視して、Iは☆で表すことにします。
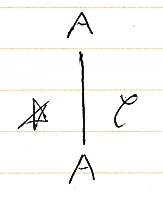
対象 A, B∈|C| に対応する関手 A~, B~:I→C があるとき、射 f:A→B in C に対応する自然変換 f~::A~⇒B~:I→C を次のように定義できます。
- (f~)0 = f :A~(0)→B~(0) in C
この自然変換f~を射fの代わりに使います。絵を描くときは、f~とfを同一視します。
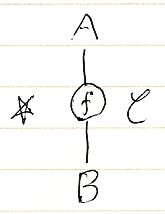
対象Aに対する恒等射 idA = A^ は、関手A~の恒等自然変換IDA~として描きます。既に述べた恒等自然変換の描き方に従い点線のマルか、id(小文字)と記入したオダンゴを使います。
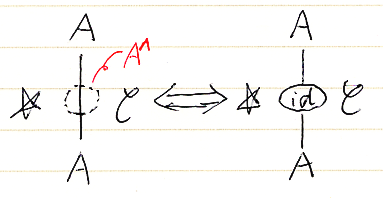
対象/射の格上げと一般の関手/自然変換を区別するために、次のルールを適用します。
- アルファベットの初めのほうの大文字 A, B, C などと、終わりのほうの大文字 X, Y, Z などは対象を表すとする。
- 小文字 f, g, h などは射を表すとする。
この約束に従えば、一番左の面のラベル☆は省略できます。また、注目してない面(圏)のラベル(名前)は適宜省略します。例えば、次のような省略が可能です。
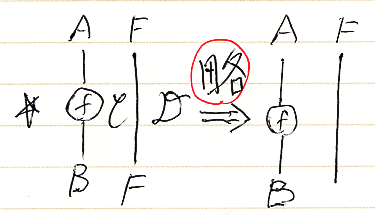
ここから先では、面のラベル=圏の名前を省略するので注意してください。
対象と射の格上げは、絵算のなかで最も重要なテクニックです。以下の記事でも解説しています。
図式順記法と混合記法
今まで紹介した図の描き方では、横方向は左から右、縦方向は上から下に描きます。この描き方と相性が良いテキスト記法が図式順記法〈diagrammatic order notation〉です。世間では、図式順と逆方向に書き並べる反図式順記法が多く用いられています。図式順記法/反図式順記法で使う演算子記号は次のように約束します。
| 演算 | 反図式順演算子記号 | 図式順演算子記号 |
|---|---|---|
| 射の結合 | |
; |
| 関手の適用 | 丸括弧 | . |
| 関手の結合 | ・ | * |
| 自然変換の適用 | 下付き添字 | . |
| 自然変換の縦結合 | |
; |
| 関手と自然変換のヒゲ結合*2 | ・ | * |
| 自然変換の横結合 | ・ | * |
詳しくは次の記事を参照してください。
この記事では原則的に図式順記法を用いますが、世間とあわせるためにしばしば反図式順記法への翻訳をします。また、図式順と反図式順が混じった書き方もします。例えば、関手の結合を図式順で、対象への適用を反図式順にすると (F*G)(A) という書き方になります。
- (F*G)(A) = A.(F*G) = (G・F)(A)
図式順記法では、自然変換の成分をA.αと書きますが、下付き添字にするαAも便利なので使います。αA.Fは、下付き添字内に図式順記法が使われています。
絵図とテキストにおける方向問題と、どの方向にも対応するためのトレーニング法は、以下の記事にあります。
対象A(の格上げ)を関手Fに入力すること(適用)は、A.Fと書きますが、対応する絵は次のようです。
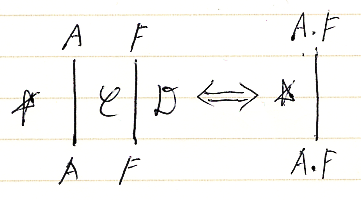
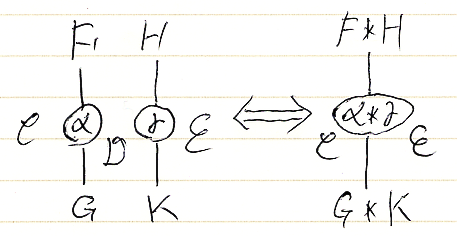
A.(F*G) = (A.F).G = A.F.G は次のようです。(反図式順記法なら、(G・F)(A) = G(F(A)) です。)
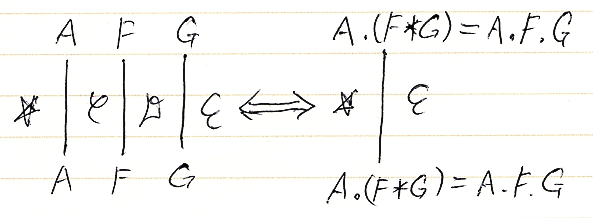
絵の上では、'.'と'*'の区別がなくなり、単に横に併置されるだけになります。
以下の絵図等式は示唆に富んでいるので是非に理解してください。
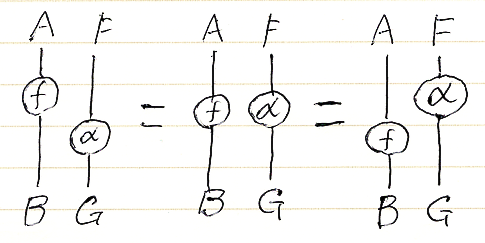
この絵は、αが自然変換である条件を表しています。順に見ていきましょう。
- 左側の上半分は、射fと関手Fの横並びなので f.F を表す。
- 左側の下半分は、対象Bと自然変換αの横並びなので B.α を表す。
- 左側全体では、(f.F);(B.α) を表す。反図式順なら αB
F(f) 。
- 右側の上半分は、対象Aと自然変換αの横並びなので A.α を表す。
- 右側の下半分は、射fと関手Gの横並びなので f.G を表す。
- 右側全体では、(A.α);(f.G) を表す。反図式順なら G(f)
αA 。
- 左右が等しいので、(f.F);(B.α) = (A.α);(f.G) 。反図式順なら αB
F(f) = G(f)
αA 。
- これはαが自然変換変換である条件そのもの(可換図式と比較してみて)。
- まん中の、射fを自然変換αに入力すること(適用)は、f.α := (f.F);(B.α) = (A.α);(f.G) と定義する。
絵算で何をやるのか
これで絵算の準備はできたので実際の計算をしてみましょう。で、何を計算するの? -- 随伴に関する計算です。前回の記事の続きです。
随伴系〈adjoint system | adjunction〉を単位/余単位のニョロニョロ関係式で定義して、ニョロニョロを使った計算をするのは良い例題です。しかし、これは割と簡単です。なぜなら、ニョロニョロは絵算とそもそも相性が良いからです。
ここでは、随伴系をホムセット同型方式で定義して、そこからニョロニョロ関係式を導いてみます。通常、ここはテキストの等式的計算で頑張るのところですが、絵を使ってみます。なんでそんなことをするか? 以下に説明します。
ホムセット同型方式の定義では、ホムセットのあいだの同型写像 ΦA,X:C(F(A), X)→D(A, U(X)) が中心となります。この写像(の族)の存在だけでは随伴系にはならず、随伴構造として大事な情報は、Φの自然性のなかにエンコードされています。
Φの自然性〈naturality〉とは、Φが自然変換であるという事実です。「圏論の随伴をちゃんと抑えよう // 転置と反転置」で述べた方法で、自然性(=自然変換の条件)は、射、関手(FとU)、Φが混じった等式として取り出せます。次のような等式でした。
- v∩;U(g) = (v;g)∩
- f;w∩ = (F(f);w)∩
- s∪;g = (s;U(g))∪
- F(f);t∪ = (f;t)∪
一見して意味不明です。これらの等式はいったい何を意味しているのでしょうか? 絵に描くと事情が分かります。
先回りして言ってしまうと、4つの等式は、ニョロニョロ関係式を切り刻んだミクロ・ルールなのです。仮にニョロニョロ関係式が“本来の存在”だとしましょう。自然変換に関するグローバルな等式であったニョロニョロ関係式が、ホムセットごとに局所化・断片化されて埋め込まれた姿が4つの等式です。
我々がやるべきことは、局所化・断片化された等式群を繋ぎ合わせ・編み上げて、グローバルなニョロニョロ関係式を再構成することです。
転置オペレータ/反転置オペレータとその描画
随伴系のホムセット同型方式定義では、次の同型写像が登場します。
- Φ:C(F(A), X)→D(A, U(X))
正確にはΦA,Xと書くべきですが、族〈family〉のインデックスはしばしば省略します。
「圏論の随伴をちゃんと抑えよう // 転置と反転置」において、Φ(v)をv∩と書くことにし、v∩をvの転置〈transpose〉と呼ぶことにしました。行列の転置とは関係ありません*3。圏Cの射を圏Dの射に移すので、転地(場所を移す)のほうがふさわしいかも。
ホムセットのあいだの写像をコンビネータまたはオペレータと呼ぶことがあるので、その習慣に従って Φ(-) = (-)∩ を転置オペレータ〈transpose operator〉とも呼びましょう。Φは可逆だったので、Φ-1(-) = (-)∪ も定義できました。こちらは反転置オペレータ〈{untranspose | opposite transpose | optranspose} operator〉です。
v∈C(F(A), X) なら v:F(X)→X in C と書けますが、図式順A.Fを使って v:A.F→X in C と書くことにします。これだけの変更でも絵図(下)との対応が格段に楽になります。vに対する転置v∩の図示は、転置オペレータの記号'∩'と同様な形の“曲がったワイヤー”を取り付けます。反転置オペレータでは'∪'の形の“曲がったワイヤー”を使います。
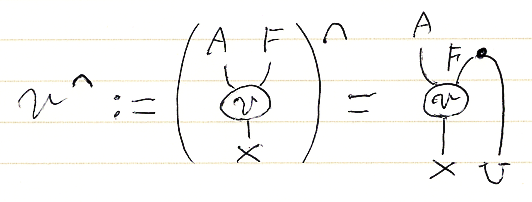
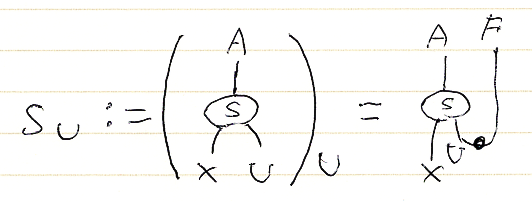
この描画法は唐突で腑に落ちないかも知れません。実は、上記描画の約束は後知恵から決めています。「転置オペレータと反転置オペレータが互いに逆であることは、ニョロニョロ関係式の局所版*4である」という事実(後知恵)と符合するように、曲がったワイヤーを繋いでいるのです。曲がったワイヤーの実体は単位('∩'の形)と余単位('∪'の形)です。
転置オペレータを使った単位の定義 ηA := (idA.F)∩ と、反転置オペレータを使った余単位の定義 εX := (idX.U)∪ は次のように図示されます。
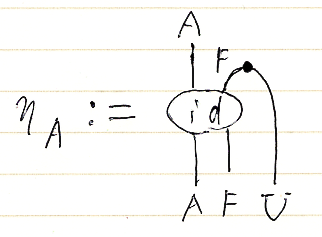
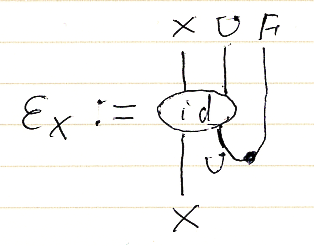
転置と反転置が互いに逆であることの表現の一例として (ηA)∪ = (idA.F)∩∪ = idA.F がありますが、それは次のように図示されます。
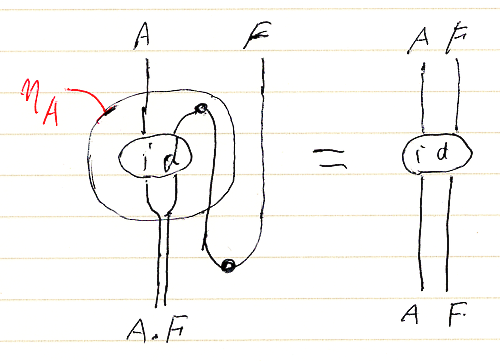
これを見ると、上付き∩と下付き∪がキャンセルする様〈さま〉が、なるほどニョロニョロ(ワイヤーの引き伸ばし)だと分かるでしょう。
転置と反転置の自然性
「圏論の随伴をちゃんと抑えよう // 転置と反転置」において、ホムセット同型Φの自然性(自然変換であること)から、次のような等式を導きました。(図式順記法に直して書きます。)
- g:X→Y in C, v:A.F→X in C に対して、v∩;g.U = (v;g)∩
- f:A→B in D, w:B.F→X in C に対して、f;w∩ = (f.F;w)∩
- g:X→Y in C, s:A→X.U in D に対して、s∪;g = (s;g.U)∪
- f:A→B in D, t:B→X.U in D に対して、f.F;t∪ = (f;t)∪
これらの等式を、今まで説明してきた描画法で描いてみます。テキストにも絵にも、赤で“まとまり”をつけるようにしたので、色をヒントにしてテキストと絵の対応を追ってみてください。
1. [v∩];[g.U] = [v;g]∩
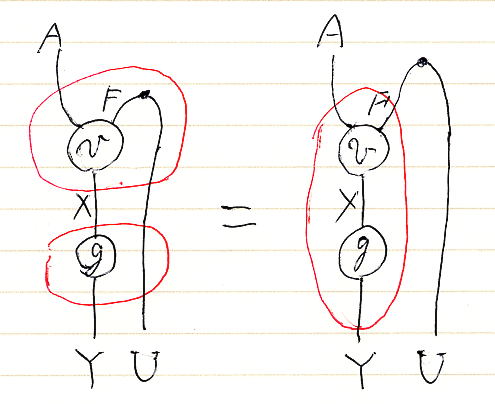
2. f;[w∩] = [f.F;w]∩
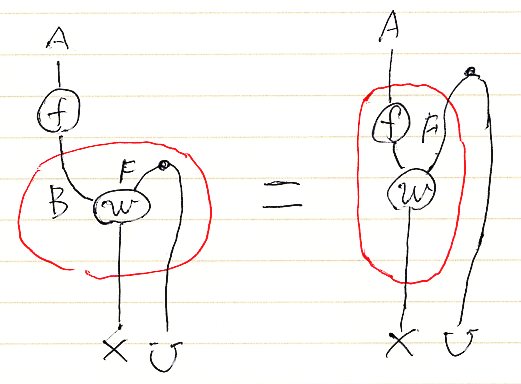
3. [s∪];g = [s;g.U]∪
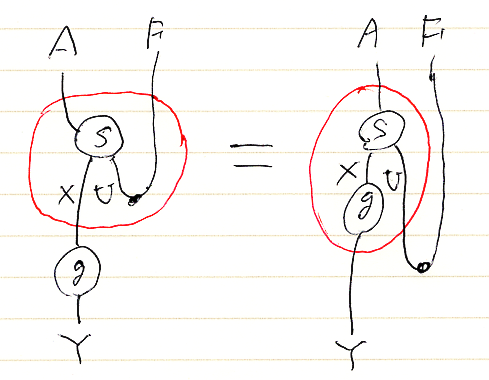
4. [f.F];[t∪] = [f;t]∪
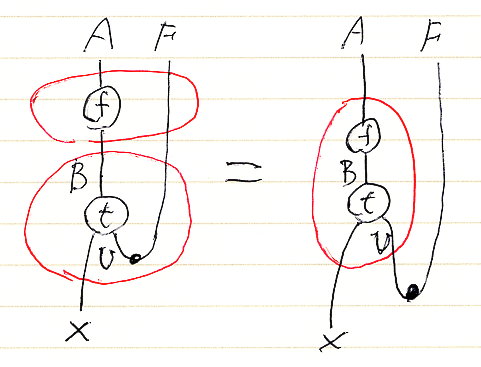
これらの絵図等式では、描画の都合で等号の左右の絵を少し変形してますが、実際には左右に完全に同じ絵(コピー)を置いてもいいのです。
等式の左右で変化するのは絵そのものではありません。(少なくともトポロジカルには)同じ絵に対して、赤枠で描いた“まとめ方”、“どこから見るか”を変えているだけなのです。目視によるフォーカスエリアと視線移動を等号の左右で変えるのです。レイアウトを変えて描くのは、正しいフォーカスエリア/視線移動を促〈うなが〉す目的です。
等号の左右でトポロジカルには何も変わってないので、「確かに同じだ」という強く自然な認識が得られます。「絵算が事態を自明化する」とはこういうことです。(「絵算の威力をお見せしよう」にも同様な例があります。)
上記の絵図等式を組み合わせると、対象・射・関手・オペレータを組み合わせた絵に対して、幾つかの“まとめ方”があり、それらが同じであることが分かります。例えば、次の絵を考えましょう(テキストで書けば (f.F;v;g):A.F→Y)。
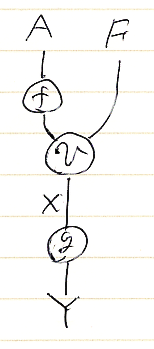
この射に対して転置オペレータ(-)∩を作用させます。このとき、射を構成するどの部分に転置オペレータを作用させるかの自由度(選択肢)があります。以下の絵では、転置オペレータを作用させる部分〈operand | 被作用部〉を赤で囲っています。どこに作用させても結果は同じです。
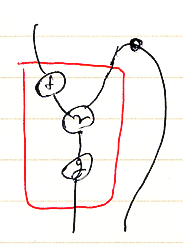
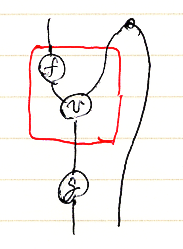
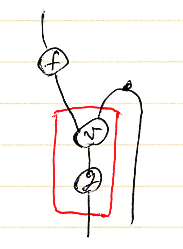
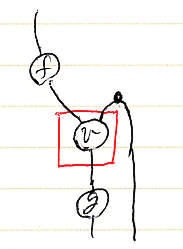
幾つかの絵が事実上同じこと(絵図等式)をテキストで書くとどうなるかは練習問題とします。絵とテキストを比較してみてください。
ホムセット同型からニョロニョロへ
前節の描画法は、ニョロニョロ関係式を先取りしています。転置/反転置オペレータを、ケーブルを曲げる操作に対応させた時点で、単位/余単位とニョロニョロ関係式がちゃっかり導入されてます。後知恵からの天下りな定義とのそしりを免れません。
しかし、形式的・論理的なスジとしては、ホムセット同型Φ(転置オペレータ)から単位/余単位とニョロニョロ関係式を絵図なしで導くことができます。先に示した4つの等式達は、Φの自然性の書き換えに過ぎないので、当然ながら絵図なしでも意味を持ちます。
- g:X→Y in C, v:A.F→X in C に対して、v∩;g.U = (v;g)∩
- f:A→B in D, w:B.F→X in C に対して、f;w∩ = (f.F;w)∩
- g:X→Y in C, s:A→X.U in D に対して、s∪;g = (s;g.U)∪
- f:A→B in D, t:B→X.U in D に対して、f.F;t∪ = (f;t)∪
これらの等式を使って、以下の等式を示せばいいわけです(「圏論の随伴をちゃんと抑えよう // ニョロニョロ方式の定義」参照)。
- εF(A)
F(ηA) = idF(A)
- U(εX)
ηU(X) = idU(X)
一番目のほうを示してみます。反図式順記法で見にくいので、見やすく書き換えます(混合記法です)。
- ηA.F ; εA.F = idA.F
左辺 = ηA.F ; εA.F // 定義 εA.F = (idA.F.U)∪ より = ηA.F ; (idA.F.U)∪ // 自然性の4番目の等式を使うと = (ηA ; idA.F.U)∪ // 恒等射を消して = (ηA)∪ // (ηA)∪ = (idA.F)∩∪ = idA.F だから = idA.F
以上は完全に等式的計算なので、ホムセット同型Φを使った定義からニョロニョロ関係式が導けました。絵算は使ってません。
「絵算は使ってません」 -- …… 実は、上の計算も僕は絵算でやってるんですけどね、ダハハハ。だって、テキスト記法は見通しが悪く操作もスムーズじゃないので、計算出来ないんだもん。上のテキスト計算に対応する絵は次のようです。赤で注釈を入れてます。
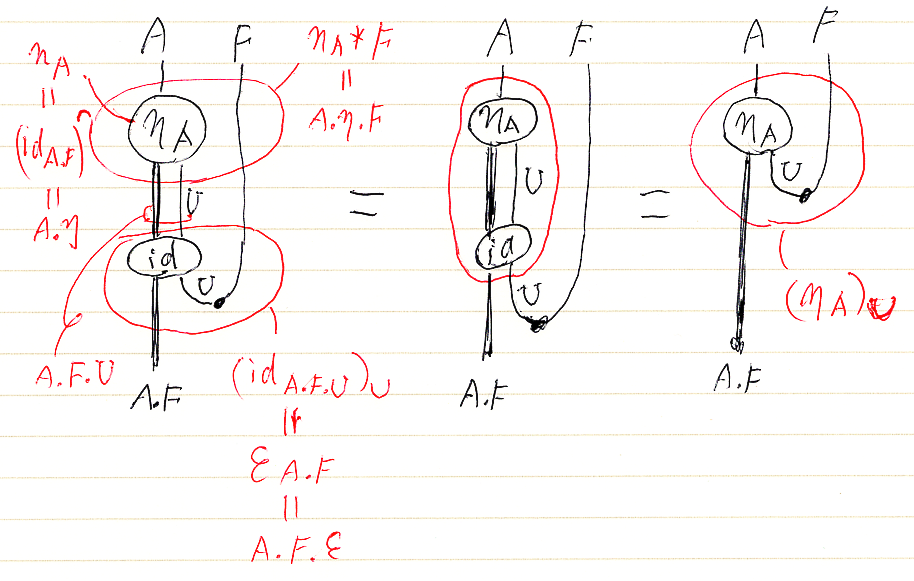
絵算のススメ
僕の個人的な想定としては、随伴や双対の背後には図形的な実体と現象があるのだと思っています。図形の話なので、絵を描いて語るのが自然でしょう。テキストによる表現と計算を使わざるを得ないのは、活字と組版の技術的な制約に縛り付けられている、という事情でしょう。
そんなことは次の記事で書いたことがあります。
いずれにしても、絵算は有効に機能します。もっと厳密で詳しい話としては、ダニエル・マースデン(Daniel Marsden)の解説があります。