スタック図の逆襲 - 檜山正幸のキマイラ飼育記 (はてなBlog)

だいぶ昔ですが、2次元の圏に関する描画に、スタック図という描画法を使っていました。例えば、2006年に書いた次の文書でスタック図も描いています。

ストリング図による複合モナドの計算 (1) *1

ストリング図に比べて特にメリットがないので、スタック図を描くのはやめてしまいました。スタック図は（僕のなかでは）葬り去られた存在でした。

しかし、最近事情が変わって、再びスタック図の出番がきたのです。そう、いま、スタック図はよみがえるのだ。

内容：

スタック図
なぜ今、スタック図なのか
事例 1：モナドの結合律
事例 2：モナド準同型射の条件
オマケ：等式を象徴する図形

スタック図

2次元の圏なら何でもいいのですが、一番お馴染みであろう“圏の圏Cat”を例として話を進めます。

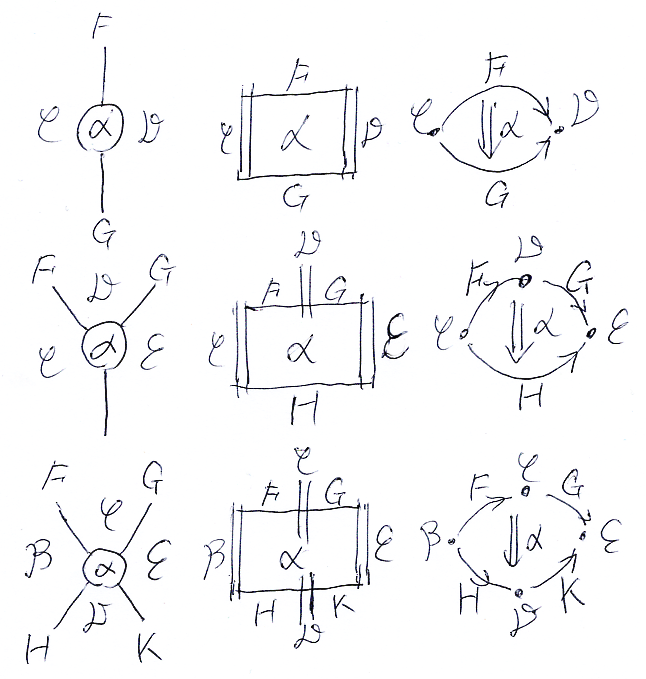
スタック図は、ストリング図とペースティング図の中間的な描画法で、対象〈0-射〉、射〈1-射〉、2-射を次のように描きます。

	ストリング図	スタック図	ペースティング図
対象	領域	二重線	点
射	線	線	矢印
2-射	点	領域	二重矢印

次の3つの状況を、ストリング図、スタック図、ペースティング図で描いたものを下に挙げます。Catのなかで考えます。記号 '＊_C' は、圏Cを接続点（共通境界）とする関手の図式順結合記号〈diagrammatic order composition symbol〉です。

α::F⇒G:C→D in Cat
α::F＊_DG⇒H:C→E in Cat
α::F＊_CG⇒H＊_DK:B→E in Cat

[補足]
スタック図は、サンティアゴ大学の人（複数）が使っていた記憶があります。今「サンティアゴ大学」を調べてみたら、

サンティアゴ・デ・チレ大学 - チリの大学
サンティアゴ・デ・コンポステーラ大学 - スペインの大学
サンティアゴ・デ・エステーロ国立大学 - アルゼンチンの大学

えっ、3つもあるんかい。出典を探すのは面倒そうなので諦めます。

四角形を積み上げて描くことから、「スタック図」と名付けたのは僕です。グリッド・レイアウトを使うので「グリッド図」でもいいかも知れません。

対象を二重線にしたのは今回の変更点です。サンティアゴ大学の人も僕も、対象も射も実線（一重）で描いていました。二重線にすると視認性が改善されるし、後述の“貧相なペースティング図”との相性も良くなります。
[/補足]

なぜ今、スタック図なのか

「貧相なペースティング図」で述べたように、このブログで使える描画機能（MathJax + AMScd）では、四角いレイアウトの可換図式しか描けません。が、ギリギリなんとかペースティング図（もどき）を描けます。

“貧相なペースティング図”は四角（長方形）を積み上げたレイアウトしか出来ないのです。このレイアウト上の制約はスタック図と同じです。であるならば、スタック図と“貧相なペースティング図”はほぼ同じものと考えていいでしょう。

このブログ内に絵図〈picture | diagram〉を載せるとき、ストリング図を手描きして、それをスタック図に直して、そのスタック図を見ながらTeXコードへの翻訳、という手順にすればよさそうです（めんどいけどなあー）。スタック図≒貧相なペースティング図は、ストリング図と（普通の）ペースティング図の中間的存在なので、どちらに翻訳するのも比較的に容易です（どっちつかずの中途半端、とも言う）。

また、ストリング図とペースティング図を相互に翻訳するとき、スタック図は中間フォーマットとして役に立つでしょう。レイアウト調整（見栄えの改善）を無視すれば、ストリング図←→スタック図←→ペースティング図の変換は機械的にできます。

スタック図は、論理の証明図とも類似しているので、論理と圏論を対応させるとき（例えば、カリー／ハワード／ランベック対応）にも使えそうです。

事例 1：モナドの結合律

モナドを (A, μ, η)/C in Cat という形で表しましょう。モナドの素材〈ingredient | constituent〉は：

C は圏
A は関手 A:C→C
μ は自然変換 μ::A＊A⇒A:C→C （'＊'は図式順の結合記号）
η は自然変換 η::Id_C⇒A:C→C （Id_Cは恒等関手）

モナドが満たすべき法則 -- 結合律、左単位律、右単位律のなかで、結合律だけを扱います。次が結合律です。

(μ＊A);μ = (A＊μ);μ :: A＊A＊A⇒A : C→C in Cat

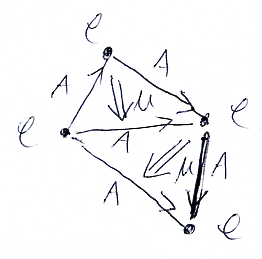
結合律をストリング図で描けば次のようです。

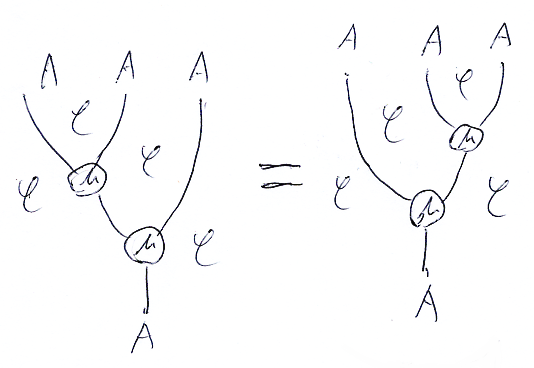
ストリング図をスタック図に描き変えるには次の手順に従います。

ストリング図の各領域を、適当な長さの縦の二重線で表す。縦二重線は圏（の名前）でラベルする。
ストリング図のワイヤー（ストリング）を、横線として描く。横線は、2つの縦二重線のあいだを繋ぎ、縦二重線に直交するように描く。横線は関手（の名前）でラベルする。
ストリング図のノード（点）は、縦二重線と横線で囲まれた四角形になる。何本かの縦二重線が、四角形に貫入するかも知れない。四角形は、自然変換（の名前）でラベルする。

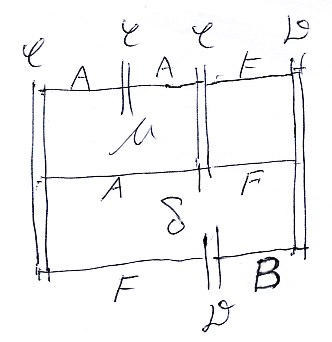
結合律の左辺をスタック図で表すと次のようになります。

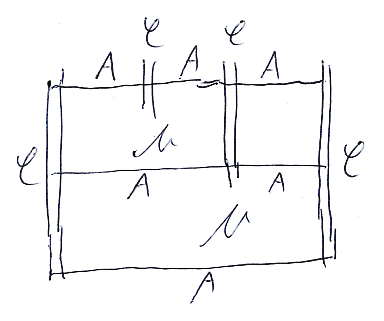
四角形の内部には自然変換（2-射）のラベルが入りますが、右上の四角形にはラベルがありません。ラベルがない四角形は退化四角形〈degenerate square〉です。四角形として描いてはありますが、実際は横線と同じです。あるいは、「恒等自然変換 ID_A のラベルが省略されている」と思ってもいいです。いずれにしても、退化四角形は横線に潰すことが可能です。

スタック図を通常のペースティング図に変換するには、縦二重線を一点に縮めます。その後に、ペースティング図の習慣に従い、横線を矢印に、領域を二重矢印に変えます。

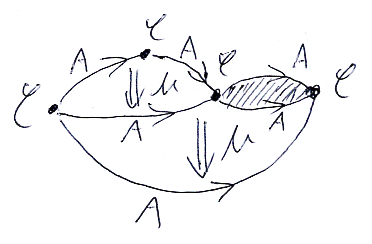
退化四角形は、ペースティング図上では退化二角形〈退化二辺形〉になります（斜線網掛け部分）。もちろん、退化二角形は一本の矢印に潰してかまいません。

ストリング図でもペースティング図でも、トポロジカルな情報を変えない範囲でレイアウト変更は自由です。カーブの矢印を直線にしてみると、次のような、四角形に対角線の図になります。太めの矢印は、潰した退化二角形です。

上のようなレイアウトにしたペースティング図により、モナドの結合律（モノイドの結合律と思ってもよい）を書いてみると：

四角形の対角線を入れ替える等式になっています。これは、三角形分割〈triangulation〉のアレクサンダー移動〈Alexander move〉（あるいは、2次元のパッヒナル移動〈Pachner move〉）のひとつです。三角形分割の移動〈変更〉は、格子2次元TQFT〈Lattice Topological Quantum Field Theory in Two Dimensions〉のFHK（福間将文, 細野忍, 川合光）理論で本質的な役割りを演じます。例えば、次の論文を参照。

Title: 2-DIMENSIONAL LATTICE TOPOLOGICAL FIELD THEORIES (22 August 2011)
Author: ELDEN ELMANTO
Pages: 31p
URL: http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Elmanto.pdf

さて、モナドの結合律左辺をアスキーアート（文字による2次元レイアウト）にすれば次のようです。僕の環境では四角に見えるようにレイアウトしましたが、環境によってはレイアウトがズレるかも知れません。

C     C     C     C
‖--A--‖--A--‖--A--‖
‖     μ     ‖     ‖
‖-----A-----‖--A--‖
‖           μ     ‖
‖-----------A-----‖

これを、頑張って MathJax + AMScd のTeXコードに翻訳します。このとき、「はてなブログで貧相なペースティング図」に書いておいたTeXマクロを使います（\catもマクロです）。

$\require{AMScd} \newcommand{\hyph}{\mbox{-}}% \newcommand{\cat}[1]{{\mathcal {#1}}}% \newcommand{\incat}{\:\: \mbox{in}\:}% \newcommand{\S}{\downdownarrows} % \newcommand{\NE}{\nearrow\!\!\!\nearrow} % \newcommand{\NW}{\nwarrow\!\!\!\nwarrow} % \newcommand{\SE}{\searrow\!\!\!\searrow} % \newcommand{\SW}{\swarrow\!\!\!\swarrow} % \newcommand{\For}{\mbox{For}\:\:} % \newcommand{\Comm}{\mbox{commutative}} % % \begin{CD} \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} \\ @| @.{\S\mu} @| @| \\ \cat{C} @= {} @>{A}>> \cat{C} @>{A}>> \cat{C} \\ @| @. @.{\S\mu} @| \\ \cat{C} @= {} @= {} @>{A}>> \cat{C} \\ \end{CD}$

\begin{CD}
\cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} \\
@|              @.{\S\mu}       @|              @|      \\
\cat{C} @=      {}      @>{A}>> \cat{C} @>{A}>> \cat{C} \\
@|              @.              @.{\S\mu}       @|      \\
\cat{C} @=      {}      @=      {}      @>{A}>> \cat{C} \\
\end{CD}

右辺を追加して、モナドの結合律を表すペースティング図の等式は次のようになります

$\begin{CD} \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} \\ @| @.{\S\mu} @| @| \\ \cat{C} @= {} @>{A}>> \cat{C} @>{A}>> \cat{C} \\ @| @. @.{\S\mu} @| \\ \cat{C} @= {} @= {} @>{A}>> \cat{C} \\ \end{CD} = \begin{CD} \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} \\ @| @| @.{\S\mu} @| \\ \cat{C} @>{A}>> \cat{C} @= {} @>{A}>> \cat{C} \\ @| @. @.{\SW\mu} @| \\ \cat{C} @>{A}>> \cat{C} @= {} @= \cat{C} \\ \end{CD}\\$

不格好ですが、なんとか意図は伝わるのではないでしょうか？

事例 2：モナド準同型射の条件

もうひとつの例を挙げましょう。(A, μ, η)/C と (B, ν, ε)/D をモナドとします。モナドのあいだの準同型射を考えることができます。ただし、モナド準同型射の定義はいくつかあります。ここでは、「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き） // 左斜め加群と右斜め加群」で述べた左斜め加群をモナド準同型射とします。モナドとモナド準同型射の圏をMndとしましょう。

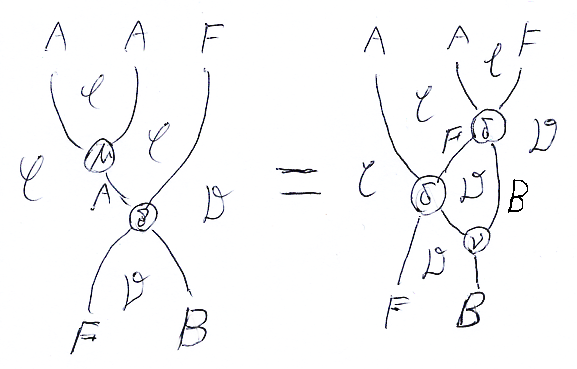
(F, δ):(A, μ, η)/C→(B, ν, ε)/D in Mnd がモナド準同型射であるとき、F, δ はそれぞれ、関手と自然変換です。

F:C→D in Cat
δ::A＊F⇒F＊B:C→D in Cat

(F, δ) がモナド準同型射である条件のひとつは次です。記号'＊'は、関手の結合、関手と自然変換のヒゲ結合、自然変換の縦結合にオーバーロード〈多義的使用〉してます。記号';'は自然変換の縦結合です。

(μ＊F);δ = (A＊δ);(δ＊B);(F＊ν) :: A＊A＊F⇒F＊B : C→D in Cat

この等式を題材にします。とりあえずストリング図で描いてみます。

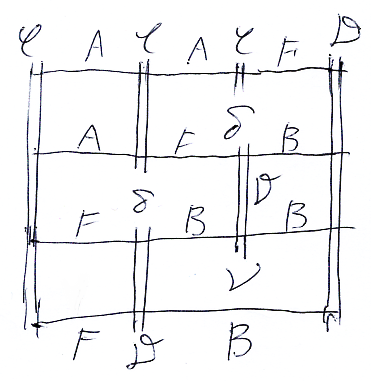
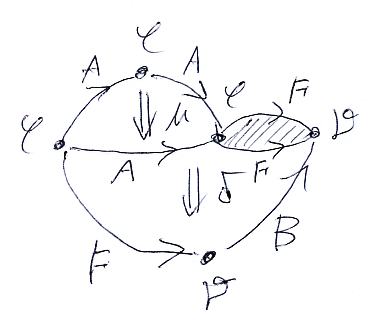
等式の左辺をスタック図で描けば：

等式の右辺のスタック図は：

頑張ってTeXコードにします。

$\begin{CD} \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} \\ @| @.{\SW\mu} @| @| \\ \cat{C} @>{A}>> {} @= \cat{C} @>{F}>> \cat{D} \\ @| @. @.{\S\delta} @| \\ \cat{C} @= {} @>{F}>> \cat{D} @>{B}>> \cat{D} \\ \end{CD} = \begin{CD} \cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} \\ @| @| @.{\S\delta} @| \\ \cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} @>{B}>> \cat{D} \\ @| @.{\S\delta} @| @| \\ \cat{C} @>{F}>> \cat{D} @>{B}>> \cat{D} @>{B}>> \cat{D} \\ @| @| @.{\SW\nu} @| \\ \cat{C} @>{F}>> \cat{D} @>{B}>> {} @= \cat{D} \\ \end{CD}$

\begin{CD}
\cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} \\
@|              @.{\SW\mu}      @|              @|      \\
\cat{C} @>{A}>> {}      @=      \cat{C} @>{F}>> \cat{D} \\
@|              @.              @.{\S\delta}    @|      \\
\cat{C} @=      {}      @>{F}>> \cat{D} @>{B}>> \cat{D} \\
\end{CD}
=
\begin{CD}
\cat{C} @>{A}>> \cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} \\
@|              @|              @.{\S\delta}    @|      \\
\cat{C} @>{A}>> \cat{C} @>{F}>> \cat{D} @>{B}>> \cat{D} \\
@|              @.{\S\delta}    @|              @|      \\
\cat{C} @>{F}>> \cat{D} @>{B}>> \cat{D} @>{B}>> \cat{D} \\
@|              @|              @.{\SW\nu}      @|      \\
\cat{C} @>{F}>> \cat{D} @>{B}>> {}     @=       \cat{D} \\
\end{CD}

オマケ：等式を象徴する図形

等式 L = R があるとき、左辺Lと右辺Rをストリング図で表すと、等式は図形から図形への変形過程を表すことになり、等式自体もひとつの図形として表現されます。例えば、モナドやモノイドの結合律は、次のような図形で表されます。

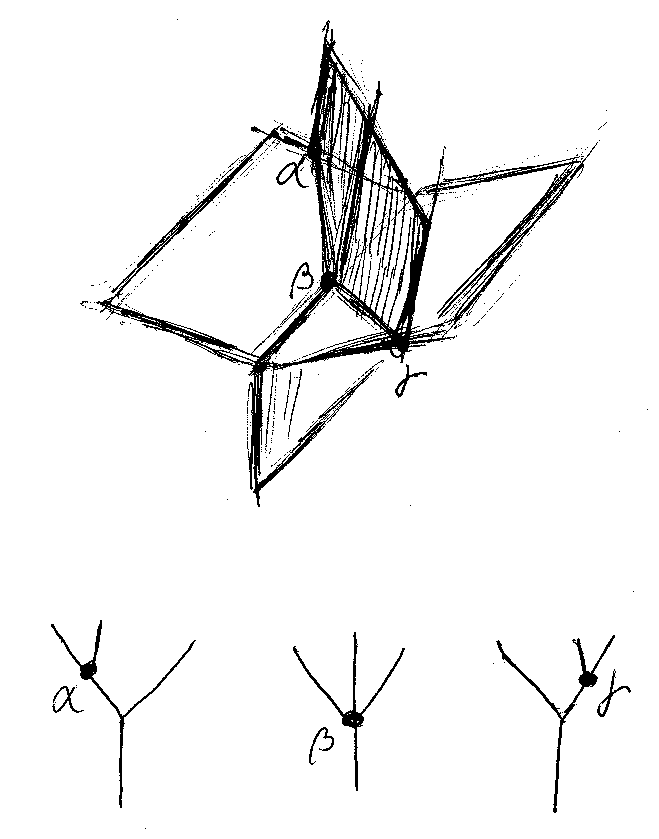
この図は、「律子からカタストロフへ」に載せたもので、同記事には他の例もあります。

今回記事の二番目の例の等式は、ベックの分配法則と関係していて、等式を表す図形はベックの分配法則とほとんど同じです。「ベックの法則と複合モナド」に載せた等式を表す図形は次のようです

ストリング図ではなくてペースティング図をベースにしても、等式を表す図形が得られます。前節の等式を例にやってみます。

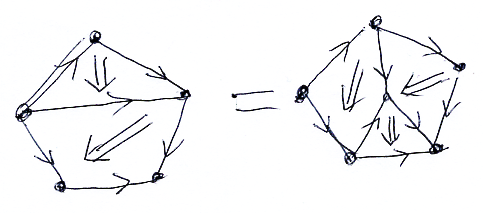
前節の等式左辺をペースティング図にすれば次のようです。

曲がった矢印を真っ直ぐな矢印にすると、これは五角形と一本の対角線になります。右辺も同様に描き変えると、五角形と1個の内点、内点と頂点をつなぐ3辺になります。ふたつの図形が等号で結ばれます。

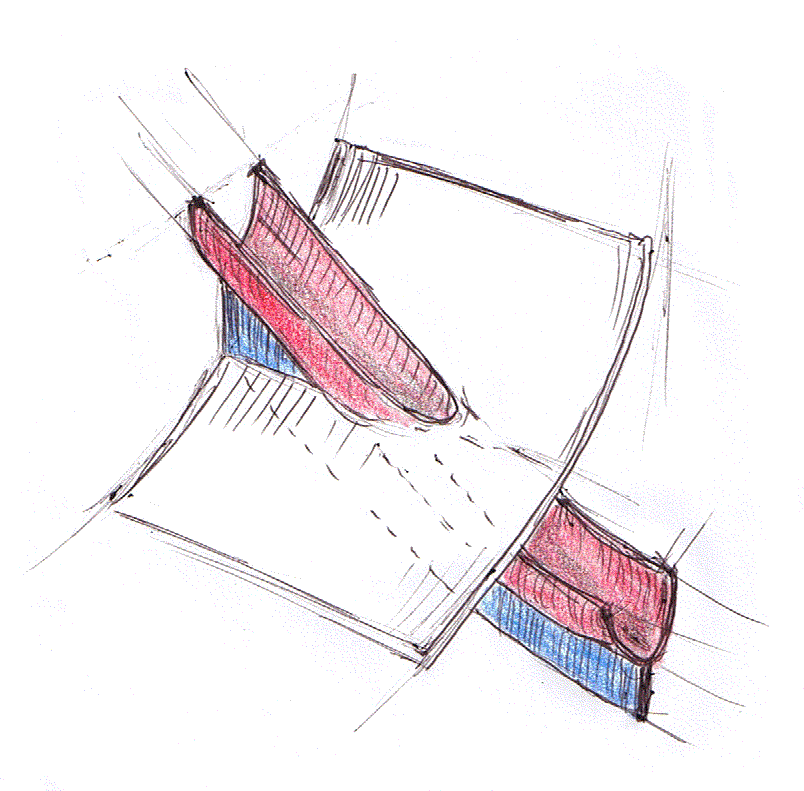
五角形を円周上の5点として描き、左辺を円柱の上面、右辺を円柱の下面として描きます。上面は、円周と一本の弦、下面は円周内にY字形（ベンツのロゴマークに似てる）になります。円柱の上面から下面への変形が、等式の左辺から右辺への変形になります。

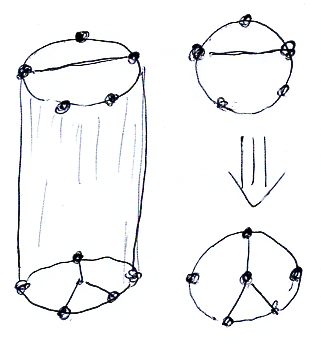
変形は円柱の表面ではなくて内部で起こります。上面の弦（線分）が下面のY字形に変化します。ねじれ〈ひねり〉を無視すれば、変形の中間は次のような図形で表現されるでしょう。

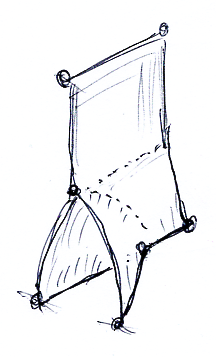
この図形は、前節の等式を象徴する図形と言っていいでしょう。

ストリング図やペースティング図を描くことによって、等式を図形の変形とみなす、さらには等式そのものをひとつの図形とみなすことができるのですね。絵を描くと楽しいでしょ。

*1:「(2)」はありません。が、「ベックの法則と複合モナド」が「(2)」に相当します。