オートマトンの定義を書き換えてみる - 檜山正幸のキマイラ飼育記 (はてなBlog)

オートマトンとラベル付き遷移系（labeled transition system）はほとんど同じものです。ここでは区別せずに遷移系全般をひっくるめて「オートマトン」と呼ぶことにします。オートマトンによりモデル化できることは多いですが、目的によっては通常の定義では使いにくいこともあります。そこで、オートマトンの定義をより使いやすい形に書き換えてみます。

結局のところ、「オートマトンとは関手です」ってオチになるのですが、これでは漠然としすぎているので、もう少し手でいじれる形も提供します。「形式言語理論のための代数」で述べた行列としての解釈とはどう関係するのか？は、また別の機会に述べるつもりです。

内容：

オートマトンの定義（普通のやつ）
普通の定義はどのへんが痒いのか
関手オートマトン
色々なオートマトン
圏を有向グラフに変えても十分
始状態の扱い
オートマトンの直和
アルファベットのケイリーグラフ

オートマトンの定義（普通のやつ）

まずは通常のオートマトンの定義から。Aをアルファベット、Sは状態空間とします。アルファベットというのは実際はなんでもよくて、適当な集合をアルファベットと呼んでいるだけです。状態空間Sも単なる集合です。アルファベットAの要素は、字（letter）、記号、ラベル、アクション、信号、終端記号とか呼び名は色々あります。応用分野や解釈が色々あるからです。

遷移写像δは、δ:A×S→S という写像です。これもどんな写像でもかまいません。アルファベットA、状態空間S、遷移写像δの三つ組 (A, S, δ) がオートマトンです。δが普通の写像のときは、決定性で全域のオートマトンとなります。部分決定性オートマトンや非決定性オートマトンもあります（後で定義します）。今は始状態や終状態は考えないことにします（後で始状態は定義します）。

ここで、上記の標準的定義を少し書き換えておきます（ただし、同値な定義です）。δ:A×S→S をカリー化した写像をφとします。つまり、φ:A→S^S、φ(a)(s) = δ(a, s) です。集合の指数表記 S^S は、S→S という写像全体の集合です。ラムダ記法を使ってφを書くなら、φ = λa.λs.δ(a, x) 、逆向きの定義は δ = λ(a, x).(φ(a)(x)) 。なんかギリシャ文字だらけだ。

(A, S, δ) と (A, S, φ) は同じことですが、以下ではφを使った形を採用します。

普通の定義はどのへんが痒いのか

先に述べた普通の定義で気に入らない点は次のようなところです。

色々な種類のオートマトンをいちいち定義しないといけないのが面倒くさい。
始状態（初期状態）や終状態の取り方も色々あるが、これに関する断り書きも面倒くさい。
複数のオートマトンを組合せて新しいオートマトンを作るとき、制約があって作れなかったり作りにくいことがある。

一番目と二番目は、オートマトンのバリエーションがイッパイあるのを博物学的に扱うのは嫌だ、ということです。部品を取り替えると新しい種類のオートマトンがバンバン出てくるようにしたいのです。

三番目は、例えば、(A, S, φ) と (B, T, ψ) がオートマトンのとき、アルファベットがAとBの直和 A + B であるオートマトンを作ろうとすると、できなくはないけど、なんか人為的な工夫が入ったりして鬱陶しい、とか。

同じようなことを何度も繰り返したり、小細工が必要なことが多いのがなんかイヤ。

関手オートマトン

オートマトン (A, S, φ) の遷移写像φは、φ:A→S^S という形でした。集合の指数 S^S を、圏論のホムセット記法で書くなら、S^S = End_Set(S) = Set(S, S) です。アルファベットAから自由生成した自由モノイドをMとすると、φの定義域はMまで自然に拡張できて、φ:M→Set(S, S) となります（拡張した写像も同じ記号で表しました）。

モノイドMは、対象が一個しかない圏とみなせます。念のためにちゃんと書くと、モノイドMから圏Cが次のように作れます。

Obj(C) = {*} （単元集合ならなんでもいい）
Mor(C) = M
dom(x) = *, cod(x) = *
x, y∈Mor(C) に対して x;y = xy （圏の結合はモノイドの掛け算）

そうすると、オートマトンの遷移写像 φ:M→Set(S, S) は、圏とみなしたモノイドMから集合圏Setへの関手です。圏の対象（1個だけ）に関しては、φ(*) = S と定義します。

以上のことから、オートマトンは関手 φ:M→Set を与えると決まってしまいます。よって、オートマトンは関手だと言ってもいいことになります。

モノイドは特殊な圏なので、その特殊性の制約は外して、一般の小さい圏Cからの関手 φ:C→Set を関手オートマトンと呼ぶことにします。スピヴァックの関手データモデルと同じ発想です。「表現、加群、前層、インデックス付き圏、導来子」あたりにチラッと書いたことがあります。

色々なオートマトン

小さい圏Cからの関手 φ:C→Set がオートマトンだと定義すると、オートマトンのバリエーションを考えるのは簡単です。集合圏Setを他の圏に取り替えるだけで色々なオートマトンが出てきます。

PtSetを付点集合（pointed set）の圏、Relを関係圏とします。φ:C→PtSet ならφは部分的決定性オートマトンです。なぜなら、PtSetは部分写像の圏と同じもの（圏同値な圏）ですから。φ:C→Rel ならφは非決定性オートマトンです。

確率写像（probabilistic mapping）の圏Probがうまく定義できたとして、φ:C→Prob は確率オートマトンということになります。Vect_K を体K上のベクトル空間の圏として、φ:C→Vect_K を考えてもいいかもしれません。K-線形オートマトンですね。Cがモノイドのときは、φ:C→Vect_K はモノイドの線形表現になります。

実用上も意味がありそうだと思っているのは、距離空間の圏を値の圏に取ることです。距離空間の圏をMetとすれば、φ:C→Met は距離オートマトンです。距離空間の圏の射としては、例えば、距離が増大しない連続写像 f:X→Y を取ればいいでしょう。

d(f(x), f(y)) ≦ d(x, y)

あるいは、K, E（K ＞ 0）を定数として、距離が一次式で評価可能な写像とか。

d(f(x), f(y)) ≦ K×d(x, y) + E

圏を有向グラフに変えても十分

伝統的なオートマトンに話を戻すと、φ:A→Set(S, S) のAはアルファベット（記号の集合）であり、モノイドではありません。必要があれば、M = A^* と自由モノイドを作って、φをMまで拡張します。つまり、自由モノイドだけを考えるなら、その生成系Aを示せば十分です。

同様に自由圏だけを考えるなら、生成系となる有向グラフGを考えれば十分です。必要があれば、Gから自由生成された圏（有向グラフのパスの圏）Cを作ればいいのです。そこで、簡略化した関手オートマトンの定義として、有向グラフGからグラフとみなした圏Cへのグラフ準同型写像 φ:G→C をC-オートマトンとします。

オートマトン φ:G→C では、有向グラフGの頂点を圏Cの対象に割り当て、Gの有向辺を圏Cの射に割り当てます。φは、関手から結合に関する条件を忘れたものです。有向グラフを恒等射と結合がない圏と考えるといいでしょう。なので、有向グラフに関しても圏の記法を借用することにします。

Gの辺の集合を同じ記号Gで表す。
Gの頂点の集合を |G| で表す。
辺fの始点を dom(f) で表す。
辺fの終点を cod(f) で表す。

従来のアルファベットAを有向グラフにするのは次のようにします。

|A| = {*} とする。
a∈A に対して、dom(a) = cod(a) = * とする。

このようにして作ったグラフでは、Aの要素はすべて単一頂点の自己ループ辺となるので、Aのループグラフと呼ぶことにします。

[追記]「関手オートマトンを説明する記号法に大いに悩む」で描いたループグラフの絵をこちらにも流用しておきます。

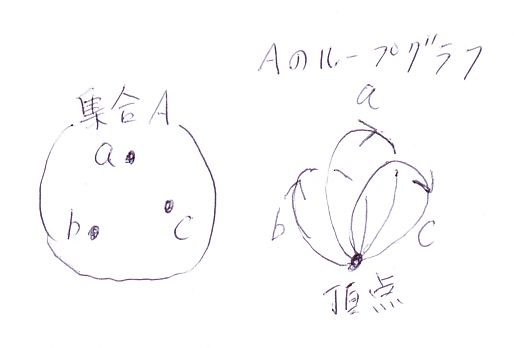
[/追記]

始状態の扱い

オートマトンの状態空間Sの始状態 s0∈S を特定するとします。アルファベットをAとして、始状態付きのオートマトンは次のように定義できます。

有向グラフの頂点集合を {0, 1} の二元集合として、0→1 の辺がただ一本あるとします（それをiとします）。有向辺の集合を A' = A∪{i} として、dom, codは次のように定義します。

dom(i) = 0, cod(i) = 1
a∈Aに対して、dom(a) = 1, cod(a) = 1

オートマトンの遷移写像 φ:A'→Set は次のように定義します。

φ(0) = {*} （単元集合）
φ(1) = S （状態空間）
φ(i) = (f:{*}→S, f(*) = s0)
φ(a) = (S→S の写像)

Set以外の圏でも似たようにして、始状態を有向グラフの一部に含めてしまうことができます。

オートマトンの直和

AとBはアルファベットとして、既に述べた方法でループグラフとみなした上で、2つのオートマトン φ:A→Set、ψ:B→Set を考えます。それぞれの状態空間は、φ(*) = S、ψ(*) = T とします。

AとBはグラフなので、グラフの直和 A + B を作ることができます。A + B の頂点集合は二元集合です。ξ:(A + B)→Set は、A上ではφ、B上ではψとして素直に作ることができます。グラフ A + B の頂点が2つあるので、状態空間も2つ（SとT）あるだけです。特別な工夫は何も要りません。必要なら、関手ξの余極限を取って考えてもかまいません。

A + B

= {*1, *2} として、*1はAから来た頂点、*2はBから来た頂点とします。ξ(*1) = φ(*) = S、ξ(*2) = ψ(*) = T ですが、S = T なら *1 と*2を同一して1頂点にすることができます。

あるいは例えば、*1→*2 の辺を付け加えると、ξは、状態空間Sから別の状態空間Tに移る遷移を持つオートマトンになります。このように、異なる状態空間のあいだを飛び移る遷移は、従来の方法だと定式化しにくいものでした。

アルファベットのケイリーグラフ

Aがアルファベットのとき、Aから単一頂点のループグラフを作ることができますが、他の方法でアルファベットAをグラフ化することもできます。

まず、Aから自由モノイドA^*を作ります。これがグラフの頂点集合です。Aが空でないないなら頂点集合は無限集合になります。

次に辺集合ですが、A^*×A を辺集合にします。A^*×A の要素を (β, a) のように表します。グラフのdom, codは次のように定義します。

dom(β, a) = β
cod(β, a) = βa （列βにaをappendした列）

以上の手順で作られたグラフをモノイドA^*のケイリーグラフ（Cayley graph）と呼びます。自由モノイドA^*はアルファベットAから決まるので、アルファベットのケイリーグラフといってもいいでしょう。Aが単元集合のとき、Aのケイリーグラフの頂点集合はNと同型になり、辺は、nと(n + 1)を結ぶ形となります。Aが二元集合なら、Aのケイリーグラフは無限に伸びる二分木です。

オートマトンを、グラフGに対する φ:G→C と定義しておけば、従来のアルファベットをループグラフと解釈しようがケイリーグラフと解釈しようが自由です。グラフや圏や関手の作り方（構成法）があれば、それらを自由に使ってオートマトンを定義してよいのです。これでかなり自由度が上がります。

最後にもう一度オートマトンの定義を述べておくと：

オートマトンとは、有向グラフから圏へのグラフ準同型写像です。