関手オートマトンを説明する記号法に大いに悩む - 檜山正幸のキマイラ飼育記 (はてなBlog)

「オートマトンの定義を書き換えてみる」で説明した事情により、オートマトンとは「小さい圏から任意の圏への関手」ということになります。関手の定義域を小さい自由圏に限るなら、自由圏の生成系である有向グラフを考えて「有向グラフから任意の圏へのグラフ準同型写像」としてオートマトンが定義されます。

このように書き換えたオートマトンの定義に基いて話を先に進めようと思ったのですが、関手オートマトンと伝統的オートマトンを一緒に扱おうとすると、使う記号（英字、ギリシャ文字）が足りなくなって、記号が衝突したり混乱したり。大変に困った状況になります。

随分と悩んで記号の割り振りを考えたわけですが、苦しんだ状況や過程を記述することが説明に役立つ気がするので、その経緯を書くことにします。記号の不足はけっこう深刻です。

内容：

伝統的なオートマトン理論で使われる記号法
圏論で使われる記号法
有向グラフと指標に関する用語と記号法
自由圏の記法
オートマトンの準同型射としての自然変換
伝統的な記号法との折り合いを付ける細工
やっぱり便宜性から記号の乱用もする
関手を使うときに注意すること／大事なこと

伝統的なオートマトン理論で使われる記号法

伝統的なオートマトン理論における、典型的な記号（英字、ギリシャ文字）の使い方は次のようなものでしょう。

用語	記号	備考
アルファベット	Σ	集合
状態空間	Q	集合
始状態（初期状態）	i	i∈Q
終状態の集合	F	F⊆Q
遷移写像	δ	δ:A×Q→Q

アルファベット（基本記号の集合）を示すのになんでΣ（大文字シグマ）を使うのか？理由は知りません。この記号法の問題は、総和記号と紛らわしいことです。ここではAを使うことにします。alpahbetの'A'からですが、ラベル付き遷移系（labeled transition system）ではラベルをアクション（action）とも呼ぶので、その'A'でもあります。

状態空間に使われる文字Qもその謂れ＜いわれ＞は分かりません。stataの'S'を使ったほうが自然な気がするので、状態空間はSにします。

始状態のiはinitialからでしょうから、これでいいとします。終状態のFはfinalからでしょう。単一の状態ではなくて集合なので大文字を使うのも納得がいきます。しかし、Fは圏論で関手を表すときの標準的な文字です。バッティングを避けたい、では、halt statesからHにするか？いや待て、関手を F, G, H とすることもあります。haltはterminateとも言うからT？いや待て、状態空間 S, T としたいときは？結局、状態空間はS一文字で頑張る(？)ことにして、終状態の集合はTを採用することにします。

遷移写像のδも、クロネッカーのデルタやディラックのデルタ関数が出てくる文脈では混乱をきたすでしょうが、その心配は少ないのでδのまま使います。

まとめると、次の記号法となります。大幅には変えていません。

用語	記号	備考
アルファベット	A	集合
状態空間	S	集合
始状態（初期状態）	i	i∈S
終状態の集合	T	T⊆S
遷移写像	δ	δ:A×S→S

圏論で使われる記号法

圏論の記号の使い方も表にまとめましょう。

用語	記号	備考
圏	C, D など	イタリック大文字
対象	A, B, X, Y など	大文字
射	f, g など	小文字
関手	F, G など	大文字
自然変換	α, β など	ギリシャ文字

オートマトンは関手に過ぎないとなると、オートマトンを表すために F, G などを使いたくなります。伝統的オートマトン理論の習慣からは違和感があるでしょうが、ここは「関手的」であることを強調するために「オートマトンF」などと呼ぶことにします。

「オートマトンの定義を書き換えてみる」では、「オートマトンφ」のようにギリシャ文字小文字を使いましたが、あれはなりゆきだったで忘れます。

オートマトンFは関手ですが、その定義域としては生成系である有向グラフを考えることにします。グラフだからGを使って、F:G→Set とか。いや待て、F, G は関手（オートマトン）の意味で使うのでまずい。A, F, G, H, S, T は既に使われているから余っている文字を探して… でも、「圏の対象＝有向グラフの頂点」も大文字を使うし、文字が足りない。

そうだ、伝統的にアルファベットのために使われていたΣを有向グラフを表すために使おう。Σはインスティチューション理論で指標（signature）を表すために使われる記号です。指標はアルファベットの拡張概念ですから関連はあるのです。グラフ理論からすると異例の記号法ですが、Σ, Γ などで有向グラフを表します。総和記号と紛らわしいことには目をつぶります。

というわけで、オートマトン F:Σ→Set のように書くことにします。値を取る圏は具体的な圏を想定しているので、Set、PtSet、Rel などが登場します。

有向グラフと指標に関する用語と記号法

関手オートマトンFの定義域である有向グラフΣは、自由圏の生成系であると同時に指標としての意味も持ちます。圏論、グラフ理論、指標の理論の用語法を比較すると：

圏	有向グラフ	指標
対象	頂点	ソート
射	辺	オペレーション
域	始点	引数（パラメータ）のソート
余域	終点	値のソート

3種類の用語法／記号法を同時に使うわけにもいかないので、圏論方f式を採用することにします。指標でもあるグラフを、指標グラフと呼ぶことにして、次の圏論的記法を使います。

指標グラフ全体	Σ
辺全体の集合	同じくΣ（記号の乱用）
頂点全体の集合	\|Σ\|
個々の辺	英字小文字 eとか
個々の頂点	英字大文字 X, Yとか
辺fの始点	dom(e)
辺fの終点	cod(e)
頂点X, Yを結ぶ辺の全体	Σ(X, Y)

圏論の記法を流用することにより、複数の記法を併用する煩雑さは避けられると思います。有向グラフは、圏から恒等射と結合（合成）の概念を除いたものです。例えば、次の3つの書き方は同じことを意味します。

e:X→Y in Σ
dom(e) = X かつ cod(e) = Y
e∈Σ(X, Y)

自由圏の記法

Aがアルファベットのとき、Aから生成した自由モノイドはA^*と書きます。右肩に星印の記法はなかなかに便利です。Σが指標グラフのときも、Σから生成した自由圏を Σ^* と書くとよさそうです。

しかし、問題があります。自由圏を構成する操作は関手となりますが、それは FreeCat:Graph→Cat という共変関手です。グラフの準同型写像 g: Σ→Γ に対して、FreeCat(g):FreeCat(Σ)→FreeCat(Γ) と対応します。FreeCat(-) の略記として上付き星印を使うと、g^*:Σ^*→Γ^* ですが、上付きの星印は反変を表すのが習慣です。ここだけの記法になりますが、FreeCatの略記として下付きダイアモンドを使って、g_◇:Σ_◇→Γ_◇ とすることにします。

圏からグラフへの忘却関手をUとすると、次の随伴関係が成立します。

CAT(Σ_◇, Set) $\stackrel{\sim}{=}$ GRAPH(Σ, U(Set))

ここで、CATとGRAPHは、集合圏Setをその対象として含むような圏の圏／グラフの圏です。CATとGRAPHは、なんだか得体の知れない超巨大な圏なんで、記述を短くするための符丁くらいに思ってください。

Σ_◇のホムセットは有向グラフのパスの集合なので、次の記法も使うことにします。

Σ_◇(X, Y) = Path_Σ(X, Y)

オートマトンの準同型射としての自然変換

Σを指標グラフとして、F, G:Σ→Set を指標グラフを共有する2つのオートマトンとします。オートマトンは事実上関手なので、オートマトンのあいだの準同型射は自然変換だと定義するのが文字通り“自然”です。以下では、グラフ準同型写像とそれが生成する関手を区別しないで話します。

圏論では、自然変換をギリシャ文字小文字で表すのが習慣です。僕は α::F⇒B:Σ→Set のように書いています。自然変換αは、指標グラフΣの頂点Xごとに、写像 α_X:F(X)→G(X) を対応させるものです。そして、自然変換としての条件（図式の可換性）があります。

オートマトンの準同型射を自然変換として定義するのが妥当かどうかの議論は今はしませんが、記号法の話だけすると、ギリシャ文字小文字は別な目的に使いたいので、オートマトンの準同型射は英字小文字にします。必要があれば、指標グラフΣの頂点を下付きに添えることはするので、f_X:F(X)→G(X) のようになります。

伝統的な記号法との折り合いを付ける細工

始状態（初期状態）と終状態の集合を持つような伝統的オートマトンは、(A, S, δ, i, T) のような5つ組の形で書かれることが多いでしょう。関手オートマトンでは、A, i, T は指標グラフΣに吸収されます。指標グラフΣは次のように定義することにします。

|Σ| = {P, S, V}
Σ(P, S) = {i}
Σ(S, S) = A
Σ(S, V) = {q}
その他の辺はなし。

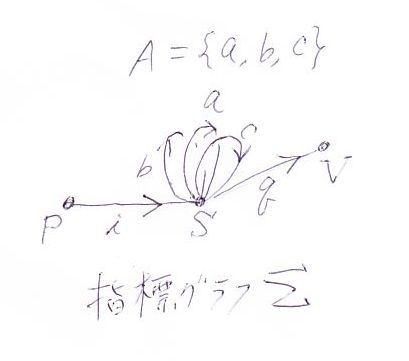
Pはpoint、Sはstate、Vはvalueから名付けています。iはinitialですね。qはqueryからです；メイヤー先生の「Command-Query分離の原則」を思い起こして欲しいのでqを使いました。Aはコマンド記号の集合なのでcommandのCでもいいのですが、先に述べたとおりalpabet, actionからのAです。

ここで注意すべきは、指標グラフの頂点 P, S, V は集合ではなくて単なる記号であることです。記号自身がグラフの頂点だと思っても、無名の頂点に記号でラベルが貼られていると思ってもかまいません。これらの記号を F:Σ→Set で写した“値”が集合なのです。さらに、次のように約束しましょう。

F(P) は常に 1 = {0} とする。
F(V) は常に B = {0, 1} とする。0と1は真偽値と解釈する。
F(S) はFごとに変わる。F(S) がオートマトンの状態空間である。

繰り返し注意しますが、Sが状態空間なのではなくて（Sは単なる記号）、F(S)∈|Set| が状態空間なのです。Σの辺であるi, q、それとAの要素もグラフの辺であり、実際の写像は次のようなになります。

F(i):1→F(S)
F(q):F(S)→B
a∈A に対して、F(a):F(S)→F(S)

1は単元集合（一点）なので、F(i)(0) は状態空間F(S)の要素となります。これが始状態を表します。一方、F(q)は状態空間F(S)から真偽値 B = {0, 1} への写像なので、1（true）の逆像 F(q)^-1(1) として終状態を定義します。F(a) は、伝統的な遷移写像を δ:A×F(S)→F(S) とすると、F(a) = λx.δ(a, x) の関係があります。

以上の議論をより馴染みのある記法にするために、F(S)をS_Fのように、関手（あるいはグラフ準同型写像）を下付き添字にして書くことにします。すると次のように言えます。

S_F は、オートマトンFの状態空間である。
i_F は、オートマトンFの始状態である。
q_F は、オートマトンFの終状態集合の特性関数（characteristic function）である。
a∈A に対して、a_F は、状態空間の変換（遷移）である。a_F:S_F→S_F

写像 i_F:1→S_F を、要素 i_F(0) と同一視すれば、i_F∈S_F とみなせます。また、T_F = q_F^-1(1) = F(q)^-1(1) と定義すれば、T_F⊆S_F という部分集合を定義します。

a∈A と x∈S_F に対して、δ_F(a, x) := a_F(x) = F(a)(x) と定義すると、伝統的な遷移写像 δ_F:A×S_F→S_F を再現できます。

Fとは別なオートマトンGに言及するときは、S_G、i_G、q_G（またはT_G）、a_G（a∈A）を使えばいいのです。

そして、オートマトンのあいだの準同型 f:F→G は、次の写像達からなります（fは関手ですから）。

f_P:1→1 （F(P) = G(P) = 1 なので）
f_S:S_F→S_G （状態空間のあいだの写像）
f_V:B→B （F(V) = G(V) = B なので）

f_Pは選択の余地がなく決まるので自明です。f_Vも常に id_B と決めておけば、オートマトンの準同型射は写像 f_S だけで決まります。であるなら、下付きのSは不要でしょう。f:S_F→S_G という状態空間のあいだの写像がオートマトン準同型射を与えます。もちろん、勝手な写像ではなくて自然変換としての条件が課せられます。

やっぱり便宜性から記号の乱用もする

S_F = F(S) 、i_F = F(i)、q_F = F(q) は辻褄があった略記法ですが、既に出してしまった T_F（オートマトンFの終状態の集合）、δ_F（オートマトンFの伝統的遷移写像）は同じ規則になっていません。T_F = F(T)、δ_F = F(δ) ではありません。全然違います。次が定義です。

T_F = q_F^-1(1)
δ_F(a, x) = a_F(x)

同じ下付きのFでも、約束が一様じゃないんですよね。まー、大目に見てもらいましょう。

もうひとつ記号の乱用をして、Fの定義域となっている指標グラフをΣ_Fと書くことにします。F:Σ_F→Set ということになります。Σの一部に（ループグラフとして）埋め込まれているアルファベットAもA_Fのように書きます。

下付きのFに共通する気分は、(ナントカ)_F が「Fのナントカ」と読めることです。

S_F -- Fの状態空間
i_F -- Fの始状態（初期状態）
q_F -- Fのクエリー関数
T_F -- Fの終状態集合
δ_F -- Fの遷移写像
Σ_F -- Fの指標グラフ
A_F -- Fのアルファベット（指標グラフの一部）

なんであれFの下付きを添えれば、伝統的な表記法 F = (A_F, S_F, δ_F, i_F, T_F) でも、関手としての表記法 F:Σ_F→Set でも書けます。

関手を使うときに注意すること／大事なこと

オートマトンという古くから知られている構造を関手という手段を使って表現してみました。従来の定義を完全に含んでいるので“互換性”はあるのですが、発想はかなり違うので、慣れないと混乱したり、違和感が拭えないかも知れません。特に次のような点に注意して考えてみてください。

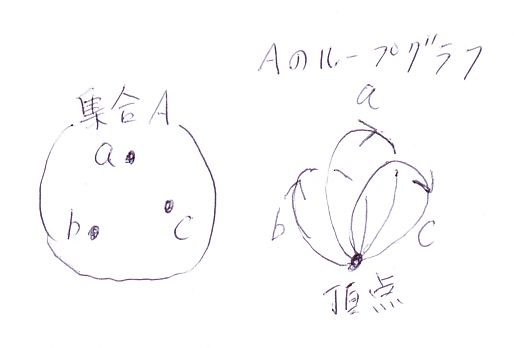
従来のアルファベットは無構造の記号の集合Aだったが、Aのループグラフを含む指標グラフΣで考える。点から線（辺）へと次元を上げて考える。下の図を参照。
指標グラフΣを圏の生成系と考えて自由圏 Σ_◇ = FreeCat(Σ) を考える。自由圏Σ_◇の射はグラフのパスなので、パスの集合 Path_Σ(X, Y) = Σ_◇(X, Y) に注目する。
単一のオートマトンではなくて、ある性質を持つすべてのオートマトンを全部一度に考える。オートマトンの集まり（圏）の社会的構造（圏的構造）に注目する。
いくつかのオートマトンから新しいオートマトンを構成する操作を見つけ出し、その法則性を探る。

今回は記号法を定めただけなので、上記の注意点をちゃんとは説明してませんが、関手の概念を応用した話をする機会もあるでしょう。