絵算(お絵描き計算、pictorial/graphical/diagrammatic calculation)で使われる絵はストリング図(string diagram)と呼ばれます。とある文書でストリンググラフ(string graph)という言葉を見たんですよね。ストリング図の同意語だろう、と思ってました。
しかし、ストリンググラフの定義のなかで"node vertex"なんて奇妙な概念が出てきて、「はぁ、なにそれ?」 -- 少し調べてみました。
内容:
ストリンググラフの起源と参考文献
ストリンググラフは、ディクソン/ダンカン/キッシンジャーの次の論文で導入された概念です。
- Title: Open Graphs and Computational Reasoning (2010)
- Authors: Lucas Dixon, Ross Duncan, Aleks Kissinger
- http://arxiv.org/abs/1007.3794
- Pages: 12 pages
ただし、この論文では「ストリンググラフ」という言葉を使っていません。オープングラフ、あるいは単にグラフと呼んでいます。後からストリンググラフという呼び名を付けたようです。
ストリンググラフを主題的に詳細に扱った論文として、キッシンジャー(Aleks Kissinger)の学位論文とメリー(Alexander Merry)の学位論文があります。
- Title: Pictures of Processes (2012)
- Aleks Kissinger
- URL: http://arxiv.org/abs/1203.0202
- Pages: 182 pages
- Title: Reasoning with !-Graphs (2014)
- Author: Alexander Merry
- URL: http://arxiv.org/abs/1403.7828
- Pages: 172 pages
どちらも長大で読む気になりません(僕は)。キッシンジャー、メリー、それとソロヴィヨフ(Matvey Soloviev)の次の論文なら短いです。
- Title: Pattern graph rewrite systems (v3 2014)
- Authors: Aleks Kissinger, Alex Merry, Matvey Soloviev
- URL: http://arxiv.org/abs/1204.6695
- Pages: 13 pages
ストリンググラフの理論は、証明支援系Quantomaticの実装のために開発された、という側面があるので、Quantomaticサイトも眺めておくといいかも知れません。(でも、Quantomaticについて知らなくても、ストリンググラフの理解に差し障りは無いです。)
ストリング図を幾何学的に眺める
ストリング図は、モノイド圏や高次圏のための計算手段ですが、ストリング図自体を研究対象とすることもあります。そのときの方向性として、とりあえず次の2つがあるでしょう(他の方向もあるかも、ですが)。
- ストリング図を図形とみて、位相的/幾何学的に調べる。
- 計算機によってストリング図を処理することを目指して、組み合わせ的に調べる。
最初に、幾何学的に調べるときの概略を例を出して説明します。
とあるモノイド圏のなかの射 f:XY→Z と g:Z→W の結合(合成) f;g:X
Y→W をストリング図で描くと次のようになるでしょう。描画方向は旗で示してます、上から下、左から右です(少しナナメってるけど^^;)。
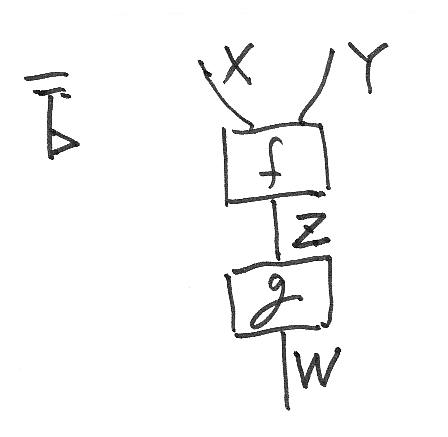
射f, gをボックスで描くのは見やすくするためで、射は0次元の点で、対象が1次元の線です。次元に忠実に描くと:
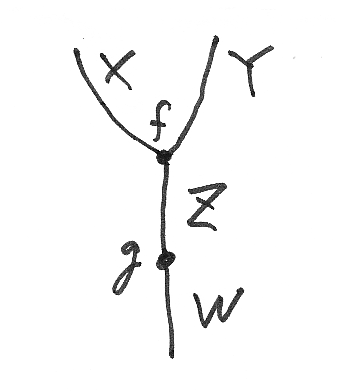
この図形は平面に描いてあるとします。すると、X, Y, Z, Wは、閉区間 [0, 1] と同相な図形なので、なめらかな埋め込み写像 x, y, z, w:[0, 1]→R2 で定義できます。射を表す0次元セルは、x(1) = y(1) = z(0) がfの点、z(1) = w(0) がgの点、となります。
外の空間(キャンバス)であるR2をアプリオリには考えないなら、[0. 1] と同相な境界付き1次元多様体を境界で貼り合わせた複体(複合的な図形)を考えて、後から必要に応じてユークリッド空間や球面に埋め込むことになります
Globularでは、高次元のストリング図を考えますが、そのような図形は、1次元とは限らない境界/角付き多様体達を、境界/角で貼り合わせた複体と考えられます。
このような見方でストリング図(サーフェイス図)を扱う方法は次を参照:
- Surface diagrams Todd Trimble
ストリング図の組み合わせ的な表現
ここから先は、高次元のストリング図(サーフェイス図)ではなくて、1次元の(本来の)ストリング図を考えます。
コンピュータは、概念的な図形(1次元多様体の貼り合わせ)をそのまま認識はできません。離散的・組み合わせ的なデジタルデータにしてあげないとコンピュータは処理できません。
グラフ理論の意味でのグラフは、コンピュータで扱った実績が十分にあるので、ストリング図をグラフで表現しましょう。パッと見では、ストリング図は既にグラフになっているように思えます。でも、実は、ストリング図とグラフは、けっこう違っているのです。
この違いを明らかにするために、グラフ理論の用語としては頂点(vertex)と辺(edge)を採用し、ストリング図の点と線は、ノードとワイヤーと呼びます。頂点=ノード、辺=ワイヤー なーんて単純なワケじゃないのです。
前節で例に挙げたストリング図を、ボックスをオダンゴにして再度描きます。
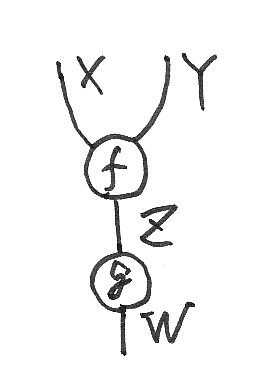
オダンゴをグラフの頂点(vertex)と考えるのは、まーいいでしょう。では、ワイヤーは辺(有向辺)でしょうか? 辺ならば、始頂点(source vertex)と終頂点(target vertex)を持たなくてはなりません。しかし、X, Yは始頂点を持ちませんし、Wは終頂点を持ちません。グラフとみなすには、ワイヤーの端点に頂点を追加する必要があります。ワイヤーの端点である頂点は、境界頂点(boundary vertex)と呼ばれます。入力側を進入境界(incoming boundary)、出力側は退出境界(outgoing boundary)と呼ぶこともあります。
射f, gの結合のときに、fの退出境界頂点とgの進入境界頂点を繋ぐことになりますが、繋いだ“跡”を残しておくと次のような図になります。
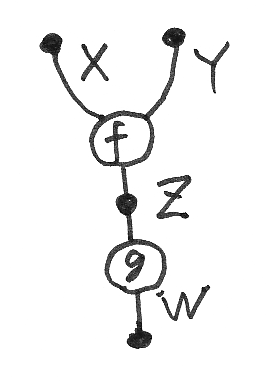
ワイヤー上にノードではない頂点が存在します。つまり、「ノードである頂点」と「ワイヤーの一部である頂点」ができます。前者をノード頂点(node vertex)、後者をワイヤー頂点(wire vertex)と呼びます。"node vertex"という奇妙な言葉は、こうして生まれたわけです。
ストリンググラフとは、今述べたような事情を考慮して、ストリング図を表現するためのグラフ構造です。頂点には、ノード頂点、進入境界頂点、退出境界頂点、ワイヤー(内部)頂点などの別があります。頂点に種類を設けることにより、ストリング図をグラフとしてエンコード出来ます。ストリング図 → ストリンググラフ のエンコードは、http://arxiv.org/pdf/1504.02716.pdf にあった次の図が分かりやすいですね(描画方向は下から上、左から右)。
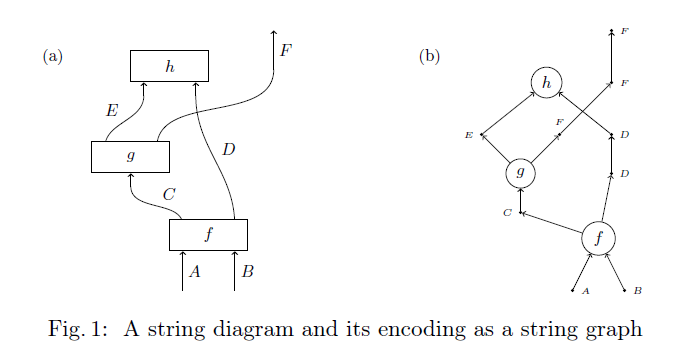
絵算=ストリング図による計算を、ストリンググラフのグラフ書き換えにより実現できそうなことは何となく予想が付きます。そうなれば、コンピュータに絵算させることが出来るはずです。実際、色々な工夫やアルゴリズムが提案され、その一部はQuantomaticやGlobularに実装されています。しかし、コンピュータ絵算はまだこれからの話です。