階層的なシステムの絵図的〈pictorial | graphical | diagrammatic〉記述として入れ子の半グラフがあります。入れ子の半グラフについては、「半グラフからシステムの記述へ」で述べました。入れ子の半グラフと概念的には同じですが、別な描画法としてバエズ/ドーラン・ツリー〈Baez-Dolan tree〉を紹介します。
入れ子の半グラフをバエズ/ドーラン・ツリーで描くと、オペラッド〈複圏〉の結合はツリーの接ぎ木で表現できます。オペラッドにおけるオペレーションの計算を絵図的に考えるという点では、この記事は以下の記事の続きとも言えます。
上記の過去記事の情報の一部を、この記事に再掲しています。
内容:
オペラッドと入れ子円板
オペラッド〈複圏〉は、n個(n = 0, 1, 2, ...)の入力を持ち1個の出力を返すオペレーションの計算を抽象化した構造です。オペラッドのオペレーションの図形的表現として、大きな円板〈大円板 | big disk〉から幾つかの小円板〈little disks〉をくり抜いた図形が使われます。小円板(穴)に別な円板をはめ込むことがオペラッド結合〈operadic composition〉です。
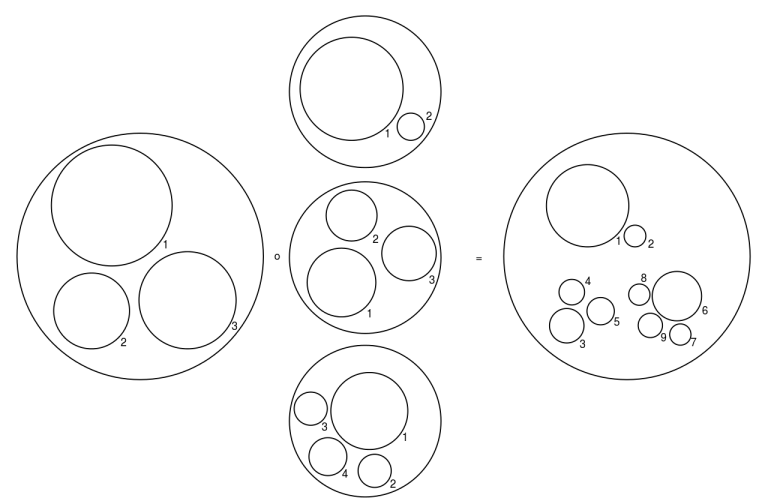
次の図は Wikipedia項目 Operad -- "Little something" operads からのコピーで、オペラッド結合を説明するものです。
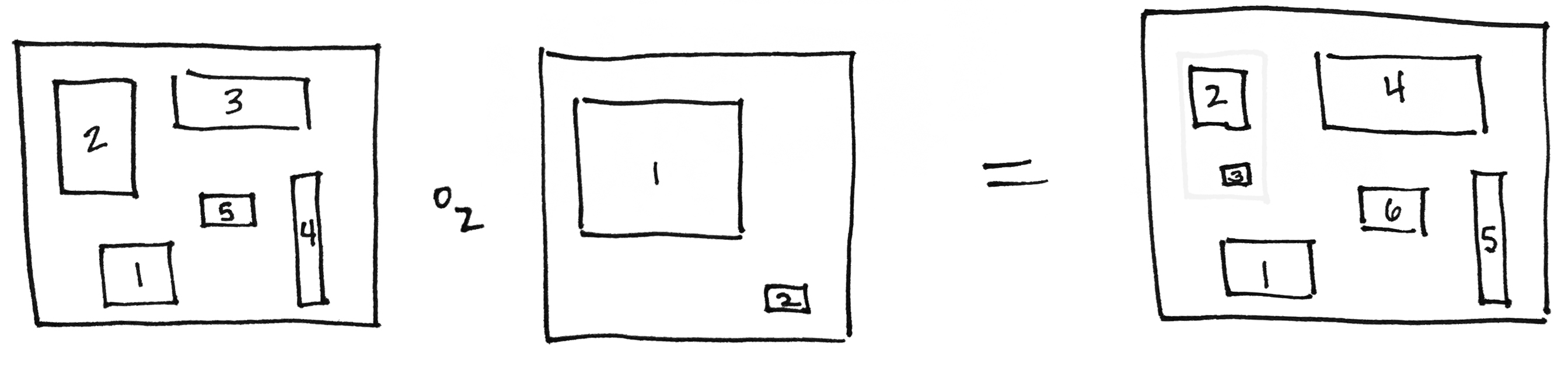
別に円板じゃなきゃいけないわけでもないので、円板の代わりに四角形〈2次元方体〉を使って描いたオペラッド結合の絵もあります(下)。左側の四角板の2番の穴に、まんなかの四角板を(縮小して)はめ込むと、右側の6個の穴を持つ四角板になります。穴の番号付け〈ナンバリング〉は適宜調整〈リナンバリング〉します。
上記の円板や四角形はのっぺらぼうで何も描かれてませんが、ポートとワイヤーを描くとストリング図〈ワイヤリング図〉になります。次の図は、スピヴァック〈David I. Spivak〉のスライド "Wiring diagrams and state machines" からコピーしたもので、入れ子の四角形にポート(四角形とワイヤーの交点)と有向ワイヤーを描いています。
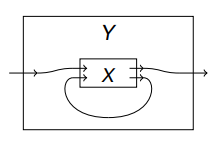
さて、「テンソルの可視化のための半グラフ // 半グラフの幾何的・位相的な定義」では半グラフを幾何的に導入しました。その後で組み合わせ構造としての半グラフを定義しました。オペラッドの入れ子円板(あるいは入れ子四角形)は目視できる図形なので幾何的です。これらの幾何的図形/組み合わせ構造は、「半グラフからシステムの記述へ」で述べたように、システムの記述に使えます。
次のような対応があります。
| 幾何的半グラフ | 組み合わせ的半グラフ | 入れ子円板 | システム |
|---|---|---|---|
| 半辺 | ポート | ポート | ポート |
| 頂点 | ボックス | 小円板 | コンポネント |
| 辺 | ワイヤー | ワイヤー | ワイヤー |
| 未定義値〈ボトム〉 | キャンバスボックス | 大円板 | システム境界 |
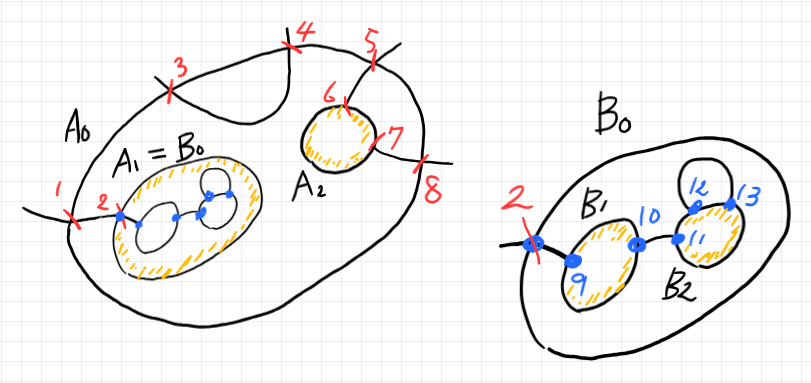
入れ子円板はオペラッドのオペレーションの表現であり、オペラッド結合が定義されていました。となると、半グラフやシステムの全体もオペラッドになり、オペラッド結合が定義できるような気がします。実際、それは可能です。
境界の情報
幾何的半グラフにおいて、ひとつの頂点に接続する半辺の集合を(その頂点の)カローラ〈corolla〉(花の冠、花びらの集まり)と呼びます。組み合わせ的半グラフでは、ひとつのボックスに所属するポートの集合がカローラに相当します。
ポートは、単なる点ではなくて型や極性を持つことがあります。ボックスを四角形なり円板なりで描くとき、ポートは境界上に並びますが、型や極性で修飾された境界になることもあります。境界上のポート達とその修飾(型や極性)を含めた情報を(ボックスの)ボーダー〈border〉と呼ぶことにします*3。ボーダーは境界の幾何的形状ではなくて、組み合わせ的情報です。ポートに修飾がないときは、ボーダーはカローラと同じことです。
ボックスの境界に乗る組み合わせ的情報であるボーダーは、スケマティック圏(「半グラフからシステムの記述へ」参照)の対象になります。具体的には次のようなものです。
- 有限集合: ポートに修飾がないとき。
- 型付き有限集合: ポートに型が付くとき。
- 極性付き有限集合: ポートに極性が付くとき。
- 極性付き型付き有限集合: ポートに極性と型が付くとき。
ボックスはコンポネント/システムだと解釈できます。そのとき、ボーダーとはインターフェイスのことです。次のような対応があります。
| 幾何的半グラフ | 組み合わせ的半グラフ | 入れ子円板 | システム |
|---|---|---|---|
| カローラ | ボーダー | ボーダー | インターフェイス |
バエズ/ドーラン・ツリー
バエズ/ドーラン〈John C. Baez, James Dolan〉は、高次圏の射の形状としてオペトープ〈opetope〉を提案しました*4。下の図はコック/ジョイアル/バタニン/マスカーリ〈Joachim Kock, André Joyal, Michael Batanin, Jean-François Mascari〉の論文にある絵です(ストリング図のテキスト化: ボックス&ポート方式」参照)。これはオペトープの表現です*5。
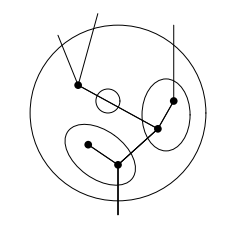
この描画法とは別に*6、オペトープの表現としてある種のツリーがあります。バエズ/ドーランのアイディアに基づくある種のツリーをバエズ/ドーラン・ツリー〈Baez-Dolan tree〉と呼ぶことにします。
「テンソルの可視化のための半グラフ」に出てきた次の半グラフをバエズ/ドーラン・ツリーに描き換えてみます。
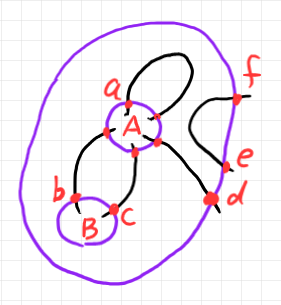
バエズ/ドーラン・ツリーは3次元空間内の曲面になります。幹や枝がチューブ(あるいはパイプ)になっているツリーなのです。
まず、もとの絵の A, B のボックス(円板)を持ち上げます。立体的輪郭を黒で描いたので、ワイヤーはグレーにしました。
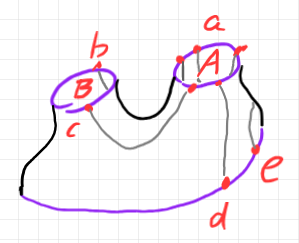
外側の円周のサイズを小さくしながら引き伸ばすと次の図形になります。チューブで作ったツリーで、ルート〈根〉とリーフ〈葉〉はポートを乗せた円周です。チューブの表面にワイヤー(グレーの線)が描かれます。
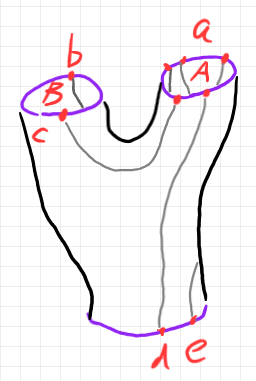
もうひとつ、「半グラフからシステムの記述へ」にあった次の半グラフをバエズ/ドーラン・ツリーに描き換えます。
以下のようになります。二股のツリーが2つあって、それを繋ぎ合わせたものです。
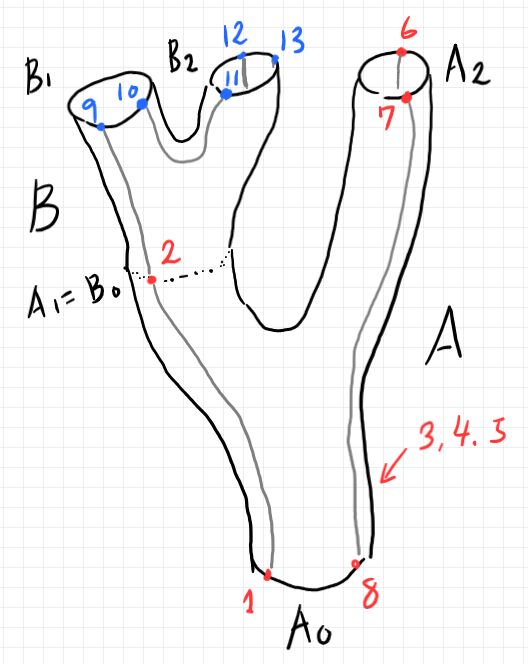
入れ子の半グラフとバエズ/ドーラン・ツリーは、同じ組み合わせ構造の別な描画法なだけで、本質的な違いはありません*7。しかし、バエズ/ドーラン・ツリーで描けば、入れ子の半グラフのオペラッド結合〈operadic composition〉が接ぎ木〈grafting〉で与えられるので、より明確で鮮明な視覚的イメージを持てるでしょう。
そしてそれから
半グラフとその変種達を応用できる分野として、とりあえず次を考えています。
- 関係データベース
- ポート指向ソフトウェア(ポートベース・コンポネントの手法)
- テンソル計算/テンソルネットワーク
- シーケント計算
もとになるモノを繋ぎ合わせて複合物を作るところは共通しています。繋ぎ合わせ方(How To Wire Them)の表現に半グラフ(やその変種)が使われます。半グラフで記述された複合物は再び“もとになるモノ”として使えるので、複合物を作る過程は繰り返し適用できます。そのことは入れ子〈nesting〉またはツリー〈tree〉で表現できます。
バエズ/ドーラン・ツリーは、“複合物を作る過程の繰り返し”を鮮明にうまく表現できます。しかし、チューブを繋げた立体的なツリーを毎回描くのは大変過ぎます! 簡略化した描画法やテキストへのエンコードを考えないといけません。テキスト化すると無駄に複雑・難解になってしまうのが悩みなんですけど ‥‥
*1:画像は https://en.wikipedia.org/wiki/Operad#/media/File:Composition_in_the_little_discs_operad.svg By Ladislav_the_Posthumous (talk) (Uploads) - Own work, GFDL, https://en.wikipedia.org/w/index.php?curid=13907966
*2:画像は https://uploads-ssl.webflow.com/5b1d427ae0c922e912eda447/5b58d5b0f848c8fd7ff73ecb_comp.jpg
*3:「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」では、境界プロファイル〈boundary profile〉、テンプレート・プロファイル〈template profile〉と呼んでいました。
*4:https://arxiv.org/abs/q-alg/9702014
*5:このような図を、コック/ジョイアル/バタニン/マスカーリは星座〈constellation〉と呼んでいます。
*6:「別に」とは見た目が違うことで、構造的には同じです。
*7:また別な描画法にケリー/マックレーン・グラフもあります。「ワイヤリング図とケリー/マックレーン・グラフ」参照。