ストリング図はボックス&ワイヤー図とも呼ばれます。「ボックス」の意味はちょっと曖昧です。「バエズ/ドーラン・ツリー: 色々な描画法」で、かなりクリアになったと思います。「注意点のまとめ」に曖昧性についても書いてあります。
ストリング図の「ボックス」は、円板表示における次のどれかになるでしょうが、どれだかハッキリしないことがあるのです。
- 円板〈disc | disk〉: 図を描くキャンバスに使う板、2次元の図形。
- 穴〈hole〉: 円板の境界円周(1次元の図形)のなかで、円板の内部にあるもの。穴と境界円周は同一視する。
- スポット〈spot〉: 円板内部の小さな領域。中身があるので穴ではない。
穴あき円板のキャンバスにワイヤリング図(ワイヤーに向きがないかも知れないストリング図)が描かれます。場合により、穴でもスポットでもないキャンバスの地の部分が意味を持つかも知れません。
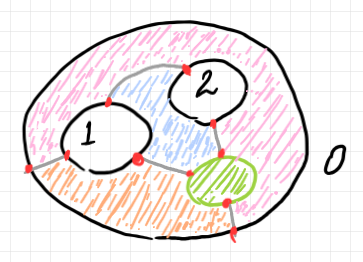
上の図で、1番と2番は穴の円周、0番は外部境界円周です。緑色はスポットで、ピンク、水色、薄いオレンジの領域はエリア〈area〉です。
穴(境界円周と事実上同義)がスポットやエリアと別物なのは分かるでしょう。穴あき円板は、穴あき球面と位相的には同型です(下の図)。幾何的な意味での(多様体の)境界の連結成分が穴です。円板の外部境界円周も穴のひとつです。

スポットとエリアはどう違うのでしょうか? ストリング図〈有向ワイヤリング図〉の、エリア、ワイヤー、スポットには、2-圏の射がラベルされるかもしれません。例えば次のように。
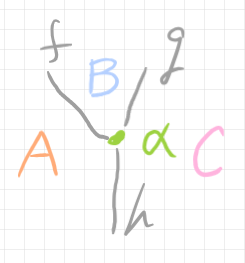
この場合:
- エリアのラベル $`A, B, C`$ は2-圏の0-射(対象)である。
- ワイヤーのラベル $`f, g, h`$ は2-圏の1-射である。
- スポットのラベル $`\alpha`$ は2-圏の2-射である。
スポットとエリアは意味的にはまったく別物です。
シーム〈seam〉は、図形としては円周で描かれます。2つの境界円周を同一視した〈重ねた〉円周がシームです。外形として同じに見えるバエズ/ドーラン・ツリーでも、シームがあるとないのでは大違いです。次の絵を見てください。
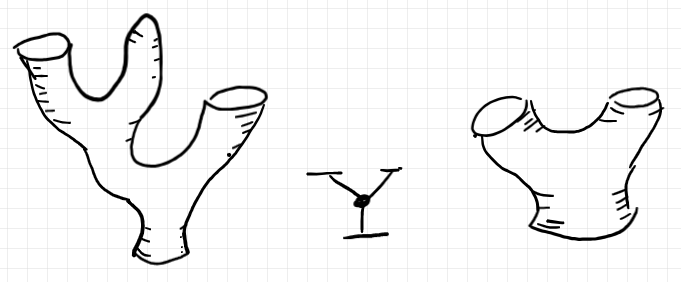
左のバエズ/ドーラン・ツリーの要約ツリーを描くとそれは、ルート円周と2つのリーフ円周からなります。位相的に同型な変形をすれば右側のバエズ/ドーラン・ツリーになり、見た目が違っても同じ構造だとみなします。
一方、シームがあると、要約ツリーの高さが2以上になります。以下のバエズ/ドーラン・ツリーは、シームの存在により高さ 3 になっています。
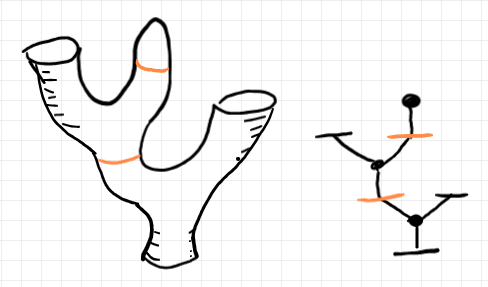
シームは、複数のバエズ/ドーラン・ツリーをどう組み合わせたか、あるいはどう組み合わせるべきかの手順の情報を含みます。シームを消すには、それ相応の操作が必要です。位相同型で変形することはただですが、シームを消すのはコストがかかる操作です。