「ハイパーグラフって要らないよなー」と、なんとなく思っていました。なんで要らないのだろう? と考えてみました。ハイパーグラフを、なんらかの事物・概念を表す描画法と捉えたとき、もっと有能で使い勝手がいい描画法があるので要らない、ってことです。「なんらかの事物・概念を表す描画法」ではない用途なら、ハイパーグラフ特有の価値があるかも知れませんが。$`\newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\In}{\text{ in } }
\newcommand{\cat}[1]{\mathcal{#1}}`$
内容:
ハイパーグラフ
ハイパーグラフ〈hypergraph〉の定義は、Wikipedia項目「ハイパーグラフ」に従います。ただし、頂点が有限個であるハイパーグラフに限ります。ハイパーグラフの事例として、Wikipediaに次の絵が載っています。
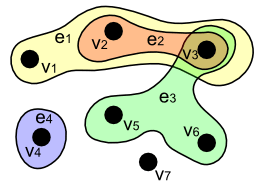
$`v_1`$ から $`v_7`$ でラベルされた黒い点が頂点〈vertex〉(またはノード〈node〉)です。$`e_1`$ から $`e_4`$ でラベルされた色付きの領域がハイパー辺〈hyperedge〉です。
ハイパーグラフは、頂点の集合(有限集合に限る)$`X`$ とハイパー辺の集合 $`E \subseteq \mrm{Pow}_+(X)`$ で決まります。ここで、$`\mrm{Pow}_+(X)`$ は、$`X`$ のベキ集合から空集合を除いたものです*1。ハイパー辺(実体は頂点の有限集合)を二元集合か単元集合に限ると、自己ループ辺を許す単純無向グラフになります。
テンソルネットワーク
テンソルネットワーク〈tensor network〉は、物性物理などで使われたりする描画法と計算法らしいです。https://tensornetwork.org/ というWebサイトがあります。僕は、物理的内容はまったく分かりませんが、絵の描き方はだいたい見当が付きます。https://tensornetwork.org/diagrams/ に絵の描き方が説明されています(分かりやすい解説です)。
絵としてのテンソルネットワークは、ストリング図〈ワイヤリング図〉です。ただし、ワイヤーに向きが付いてないので、無向ストリング図〈無向ワイヤリング図〉です。向きがある図も使うのかも知れませんが、ここではワイヤーに向きがないテンソルネットワークだけを考えます。
テンソルネットワークでは、特別なノードとしてデルタノード〈delta node〉あるいはスパイダー〈spider〉と呼ばれるノードがあります。https://tensornetwork.org/diagrams/ では、デルタノードはワイヤーと同一視して描画しないルールですが、これは困ることもあるので、デルタノードは黒丸で描くことにします。
「ダガー・ハイパーグラフ圏とドット付きワイヤリング図」で紹介したアーレクス・キッシンジャー〈Aleks Kissinger〉の描画法では、特別なノードを黒丸で描くルールを採用しています。キッシンジャーの描画法をドット付きワイヤリング図〈dotted wiring diagram | wiring diagram with dots〉として参照します(キッシンジャー自身はドット図〈dot diagram〉と呼んでますが)。
ここで使うテンソルネットワークの描画法は、ドット付き無向ワイヤリング図です。ドットはデルタノード〈スパイダー〉を表します。デルタノードは、型〈色〉と脚の数(ノードに接続できるワイヤーの数)だけで識別できます。型〈色〉を考えないときは、脚の数だけでデルタノードを識別できます。描かれた絵では、脚の数は目視で確認できるので、デルタノードには何のラベルもしなくてかまいません。
絵としてのテンソルネットワークは、半グラフです。半グラフとは、一方だけノードに接続してもう一方が開いた辺〈開放辺 | 外部辺〉を許す無向グラフです。半グラフの詳しいことは次の過去記事を参照してください。
半グラフが、開いた辺を持たない(通常の辺だけを持つ)とき閉じた半グラフ〈closed semi-graph〉と呼ぶことにします。閉じた半グラフは通常の無向グラフです。テンソルネットワークが、半グラフとして閉じているとき閉じたテンソルネットワーク〈closed tensor network〉と呼びます。
ハイパーグラフからテンソルネットワークへ
ハイパーグラフが与えられると、閉じたテンソルネットワークに描き換えることができます。ハイパーグラフの頂点はデルタノードになり、頂点の多重度〈multiplicity〉(後述)はデルタノードの脚の数になります。ハイパーグラフのハイパー辺はテンソルネットワークの通常ノード(デルタではないノード)になります。
$`(X, E)`$ をハイパーグラフとします。$`E \subseteq \mrm{Pow}_+(X)`$ であることはたいして本質ではなくて、$`x\in X`$ と $`e\in E`$ に接続関係があるかどうかが問題です。つまり、ブール係数の接続行列〈incidence matrix〉があればいいわけです。その接続行列を $`R`$ とすれば:
$`\quad R:X \times E \to {\bf B}`$
$`R(x, e) = \mrm{True} = 1`$ のとき、頂点 $`x`$ はハイパー辺 $`e`$ と接続($`e`$ に所属)していて、そうでないなら接続(所属)していません。
次の例で考えましょう。
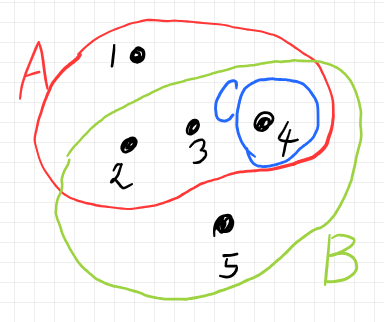
5つの頂点と3つのハイパー辺を持つハイパーグラフです。頂点が幾つのハイパー辺に含まれるか? を勘定した数を頂点の多重度〈multiplicity〉と呼びましょう。例えば、頂点 1 の多重度は 1 で、頂点 2 の多重度は 2 、頂点 4 の多重度は 3 です。
ハイパーグラフの接続行列の情報は次の絵でも表現できます*2。
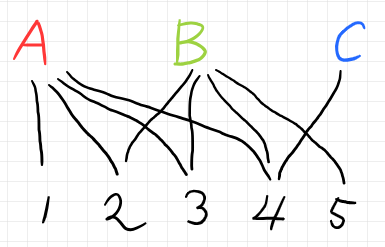
テンソルネットワークに描き換える準備に、ノードをそれらしい形にします。
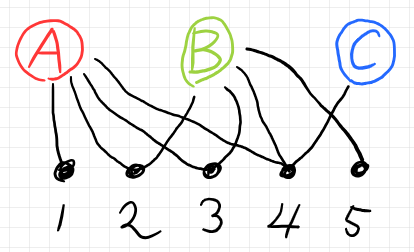
お好みのレイアウトにするとテンソルネットワークが出来上がります。
頂点から得られたデルタノード〈スパイダー〉の脚の数(次数〈degree〉とか価数〈valency〉ともいう)は、頂点の多重度に一致します。
Wikipediaの項目に、次のような記述があります。
グラフとは異なり、ハイパーグラフは紙上に図示するのが困難である。そのため、グラフ理論のような図解をされることは少なく、集合論の用語で表される傾向がある。
テンソルネットワークにすれば紙上に図示するのは容易で、図解により記述や説明ができます。
絵の描き換えの途中で使った図は、ケリー/マックレーン・グラフ(「ワイヤリング図とケリー/マックレーン・グラフ」参照)の特別なものです。テンソルネットワークは、伝統的な意味でのテンソルの絵図表現なので、絵から伝統的テンソル記法に翻訳することもできます。