ダガー・ハイパーグラフ圏とドット付きワイヤリング図 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ハイパーグラフ圏〈hypergraph category〉については、以下の記事でごく簡単に触れたことはあります。

ハイパーグラフ圏一瞥

しかし、それ以降は話題にしたことがありません。ハイパーグラフ圏をちょっと使ってみたい気がしたので、次の論文の前半をもとにして、ダガー・ハイパーグラフ圏達を対象類とする2-圏 $`{\bf DagHypCat}`$ について記述します。

Title: Finite matrices are complete for (dagger-)hypergraph categories
Author: Aleks Kissinger
Submitted: 23 Jun 2014 (v1), 19 Aug 2015 (v2)
Pages: 15p
URL: https://arxiv.org/abs/1406.5942

また、上記論文で解説されている描画法（ドット付きワイヤリング図）を紹介します。ドット付きワイヤリング図は、頂点極性とボックス（頂点のグルーピング）を持ったハイパーグラフと解釈できます。

今日はダガー・ハイパーグラフ圏の実例について述べませんが、データベースや統計・確率の話に使えそうです（それが動機）。$`\newcommand{\cat}[1]{\mathcal{#1}}
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\In}{ \text{ in } }
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\hyp}{\text{－}}
\newcommand{\twoto}{\Rightarrow}
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
%\newcommand{\Iff}{\Leftrightarrow}
`$

内容：

ダガー対称モノイド圏達の2-圏
ダガー対称モノイド圏内のダガー特殊可換フロベニウス代数
ダガー・ハイパーグラフ圏
ダガー・ハイパーグラフ圏達の2-圏
ドット付きワイヤリング図
ハイパーグラフとの関係
おわりに

ダガー対称モノイド圏達の2-圏

$`\cat{C} = (\cat{C}, \otimes, I, \alpha, \lambda,\rho, \sigma)`$ （記号の乱用）を対称モノイド圏とします。対称モノイド圏 $`\cat{C}`$ 上のダガー演算子〈dagger operator〉*1 $`(\hyp)^\dagger`$ とは：

対象類の上で恒等〈identity-on-objects〉な反変自己関手 $`(\hyp)^\dagger : \cat{C} \to \cat{C}^\op`$
厳密に対合的〈involutive〉： $`( f^\dagger )^\dagger = f`$
モノイド積を厳密に保つ。$`(f\otimes g)^\dagger = f^\dagger \otimes g^\dagger`$
$`(\hyp)^\dagger`$ は、結合律子、単位律子、対称射を逆にする：
$`\quad \alpha^\dagger = \alpha^{-1}, \lambda^\dagger = \lambda^{-1}, \rho^\dagger = \rho^{-1}, \sigma^\dagger = \sigma^{-1}`$

$`\cat{C}`$ の射 $`f`$ が $`f^\dagger = f^{-1}`$ を満たすときユニタリ射〈unitary morphism〉といいます。この言葉を使うと、4番目の条件は、対称モノイド圏の構造を与える構造射達はすべてユニタリ射であることになります。

ダガー演算子 $`(\hyp)^\dagger`$ を備えた対称モノイド圏 $`\cat{C} = (\cat{C}, \otimes, I, \alpha, \lambda,\rho, \sigma, (\hyp)^\dagger)`$ （記号の乱用）を、ダガー対称モノイド圏〈dagger symmetric monoidal category〉と呼びます。ダガー圏〈dagger category〉に対称モノイド構造が載ったものと考えれば、対称モノイド・ダガー圏〈symmetric monoidal dagger category〉という呼び名になります。

関手が、ダガー対称モノイド圏のあいだの準同型的〈homomorphic〉な関手である条件は、まずはモノイド関手であることです。モノイド関手には幾つかの種類がありますが、それについては次の記事を参照してください。

モノイド自然変換とモノイド同値関手

通常、厳密モノイド関手、強モノイド関手、ラックス・モノイド関手、反ラックス・モノイド関手と分類しますが、形容詞「強」は「テンソル強度と整合する／協調する」の意味で使いたいので、僕は形容詞「タイト」を使っています。そのことについては：

高次圏：用語法と文脈（主に2次元） // 厳密、強、ラックス、反ラックス

ダガー対称モノイド圏のあいだの関手はタイト・モノイド関手だとします。モノイド関手の一貫性射〈coherence morphism | coherence map〉はラクセイター〈laxator〉と呼びます。ラクセイターについては次の記事に書いています。

緩化子〈ラクセイター〉

ラックス・モノイド関手の場合は、

乗法ラクセイター〈multiplication laxator〉
単位ラクセイター〈unit laxator〉

を持ちます。反ラックス・モノイド関手〈余ラックス・モノイド関手〉の場合は、

余乗法ラクセイター〈comultiplication laxator〉
余単位ラクセイター〈counit laxator〉

を持ちます。

タイト・モノイド関手は、乗法ラクセイターと単位ラクセイターが可逆であるラックス・モノイド関手です。逆にした乗法ラクセイター／単位ラクセイターは余乗法ラクセイター／余単位ラクセイターになるので、タイト・モノイド関手は反ラックス・モノイド関手でもあります。

ダガー対称モノイド圏のあいだの関手 $`F:\cat{C} \to \cat{D}`$ は対称モノイド構造も保存するので、次の図式が可換になります。$`\nu`$ は乗法ラクセイターだとします。

$`\require{AMScd}
\text{For }A, B \in |\cat{C}|\\
\begin{CD}
F(A)\otimes F(B) @>{\sigma}>> F(B) \otimes F(A) \\
@V{\nu_{A, B}}VV @VV{\nu_{B,A}}V\\
F( A\otimes B) @>{F(\sigma)}>> F( B\otimes A)
\end{CD}\\
\text{commutative in }\cat{D}
`$

さらに、$`F`$ はダガー演算子を厳密に保存するとします。

$`\text{For }f: A \to B \In \cat{C}\\
\quad F(f^\dagger) = F(f)^\dagger
`$

以上の条件をすべて満たす関手 $`F`$ が、ダガー対称モノイド圏のあいだの準同型的な関手であるダガー対称モノイド関手〈dagger symmetric monoidal functor〉です。まとめると：

$`F`$ は、タイト・モノイド関手である。
$`F`$ は、乗法ラクセイターが対称射と協調する。
$`F`$ は、ダガー演算子を厳密に保存する。

$`F, G`$ を、2つのダガー対称モノイド圏のあいだの関手とすると、これらのあいだの自然変換 $`\alpha : F \twoto G`$ はモノイド自然変換だと決めます。モノイド自然変換については「モノイド自然変換とモノイド同値関手」を見てください。

構成素が揃ったので、ダガー対称モノイド圏達を対象類とする2-圏 $`{\bf DagSymMonCat}`$ を定義できます。

$`{\bf DagSymMonCat}`$ の対象〈0-射〉は、小さなダガー対称モノイド圏
$`{\bf DagSymMonCat}`$ の射〈1-射〉は、ダガー対称モノイド圏のあいだのダガー対称モノイド関手
$`{\bf DagSymMonCat}`$ の2-射は、ダガー対称モノイド関手のあいだのモノイド自然変換

$`{\bf DagSymMonCat}`$ が実際に2-圏であることを律儀に示すのは、けっこうな作業となります。今は割愛します。

単に $`{\bf DagSymMonCat}`$ と書いたときは2-圏を意味し、2-射〈モノイド自然変換〉を捨てたいときは $`\dimU{\bf DagSymMonCat}{1}`$ のように書きます。この書き方については「圏の次元調整」を見てください。

小さくないダガー対称モノイド圏も対象とした2-圏は $`{\bf DagSymMonCAT}`$ です。例えば、直積をモノイド積とする関係圏 $`({\bf Rel}, \times, {\bf 1})`$ に関係の転置をダガーとすると、小さくないダガー対称モノイド圏になります。このダガー対称モノイド圏は、2-圏 $`{\bf DagSymMonCAT}`$ の対象です。

ダガー対称モノイド圏内のダガー特殊可換フロベニウス代数

$`\cat{C} = (\cat{C}, \otimes, I, \sigma)`$ （記号の乱用と省略）が対称モノイド圏だとして、次のような $`\cat{C}`$ 内の対象・射の一式を考えます。

対象 $`A \in |\cat{C}|`$
射 $`\Delta: A \to A\otimes A \In \cat{C}`$
射 $`\bot: A \to I \In \cat{C}`$
射 $`\nabla: A\otimes A \to A \In \cat{C}`$
射 $`\top: I \to A \In \cat{C}`$

これらが一連の公理〈法則 | 条件〉を満たすとき、特殊可換フロベニウス代数〈special commutative Frobenius algebra〉と呼ぶのですが、公理は絵図〈picture | diagram〉で書いたほうが早いので、Finite matrices are complete for (dagger-)hypergraph categories から画像コピーします。

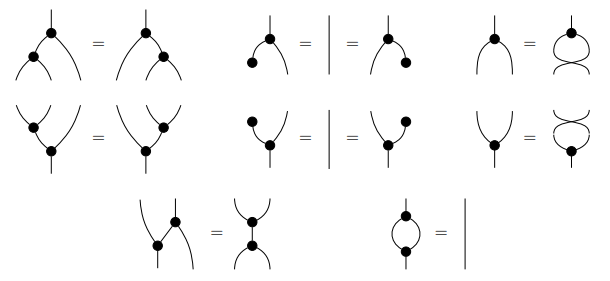
$`\Delta`$ が分岐する黒丸、$`\bot`$ が終端する黒丸、$`\nabla`$ が合流する黒丸、$`\top`$ が開始する（出発点となる）黒丸です。ワイヤーは対象 $`A`$ を表します。上側の二段は、$`(A, \Delta, \bot), (A, \nabla, \top)`$ がそれぞれ余可換コモノイド、可換モノイドになると言っています。下段の左がフロベニウス法則、下段の右が特殊性（と呼ばれる法則）です。「フロベニウス代数が特殊である（特殊性を持つ）」とは、単に下段右の法則を満たすという意味なので、誤解しないように。

特殊可換フロベニウス代数の公理は向きをひっくり返しても全体として同じなので、絵図の描画方向を“上から下”と解釈しても“下から上”と解釈しても変わりがありません。この絵を描いたキッシンジャー〈Aleks Kissinger〉は“下から上”の描画方向を採用しています。

“下から上”の描画方向は、伝統的テンソル計算の記法と整合性が取れるのですが、象形文字である $`\Delta, \bot, \nabla, \top`$ とは逆向きになってしまい、具合が悪いです。僕は通常“上から下”の描画方向を採用しています。描画方向に関するゴタゴタに興味があれば：

対称モノイド圏 $`\cat{C}`$ がダガー $`(\hyp)^\dagger`$ を持つとき、次の条件を加えると、ダガー特殊可換フロベニウス代数〈dagger special commutative Frobenius algebra〉の公理になります。

$`\quad \Delta^\dagger = \nabla\\
\quad \bot^\dagger = \top
`$

射の向きを上下方向に描くならば、ダガーにより上下が反転することになります。ダガーを二度適用すると元に戻るのは、反転を二度行うと元に戻ることだと理解できます。

「特殊可換フロベニウス代数」「ダガー特殊可換フロベニウス代数」という呼び名は長いので、SCFA、DSCFA という略称も使います。

ダガー・ハイパーグラフ圏

$`\cat{C}`$ はダガー対称モノイド圏だとします。$`A = (A, \Delta, \bot, \nabla, \top)`$ （記号の乱用と省略）を $`\cat{C}`$ 内のダガー特殊可換フロベニウス代数〈DSCFA〉とします。$`B`$ をもうひとつのDSCFA〈ダガー特殊可換フロベニウス代数〉だとして、$`f:A \to B \In \cat{C}`$ がDSCFAのあいだの準同型射〈homomorphism〉だとは、DSCFAの演算を保存することです。例えば、$`\Delta`$（余加法演算）に関して言えば、次の図式が可換になることです。

$`\begin{CD}
A @>{f}>> B\\
@V{\Delta}VV @VV{\Delta}V\\
A \otimes A @>{f\otimes f}>> B\otimes B
\end{CD}\\
\text{commutative in }\cat{C}
`$

ダガー対称モノイド圏 $`\cat{C}`$ 内のDSCFAを対象として、DSCFAの準同型射を射とする圏 $`\mrm{DSCFA}(\cat{C})`$ を構成できます。

$`A = (A, \Delta, \bot, \nabla, \top)`$ と $`B = (B, \Delta, \bot, \nabla, \top)`$ が2つのDSCFAのとき、$`A\otimes B \in |\cat{C}|`$ に載ったDSCFAを構成できます。例えば、$`\Delta`$（余加法演算）に関して言えば、おおよそ（結合律子を省略して）次のように定義します。

$`\Delta_{A\otimes B} : A \otimes B \to (A\otimes B)\otimes (A\otimes B) \In \cat{C}\\
\quad \Delta_{A\otimes B} := (\Delta_A \otimes \Delta_B) ; (\id_A \otimes \sigma_{A, B} \otimes \id_B)
`$

こうして作られるDSCFAを $`A\otimes B = (A\otimes B, \Delta, \bot, \nabla, \top)`$ （記号の乱用）と書きます。DSCFAに作用する二項演算 $`\otimes`$ により、圏 $`\mrm{DSCFA}(\cat{C})`$ をモノイド圏にすることができます。

DSCFAに対してその台対象〈underlying object〉、DSCFA準同型射に対してその台射〈underlying morphism〉を対応させる忘却関手 $`U`$ を定義できます。$`U`$ は厳密モノイド関手になります。つまり、次の等式が成立します。

$`U : \mrm{DSCFA}(\cat{C}) \to \cat{C} \\
\text{For }A, B \in \mrm{DSCFA}(\cat{C})\\
\quad U(A \otimes B) = U(A)\otimes U(B) \In \cat{C}\\
\quad U(I) = I \In \cat{C}
`$

$`U(I)`$ の引数になっている $`I`$ は、$`\cat{C}`$ の単位対象としての $`I`$ 上に載っている規準的〈canonical〉DSCFAのことです（記号の乱用）。

ダガー・ハイパーグラフ圏〈dagger hypergraph category〉とは、ダガー対称モノイド圏にハイパーグラフ構造が付いたものです。以下、ハイパーグラフ構造を説明します。

ハイパーグラフ構造〈hypergraph structure〉 $`H`$ は、ダガー対称モノイド圏 $`\cat{C}`$ の対象に、$`\mrm{DSCFA}(\cat{C})`$ の対象（$`\cat{C}`$ 内のDSCFA）を対応させる写像です。関手ではなくて写像であるところがミソです。$`H`$ は次の性質を持ちます。

$`H: |\cat{C}| \to |\mrm{DSCFA}(\cat{C})| \In {\bf Set} `$ （圏のサイズが小さいとは限らないなら $`{\bf SET}`$ を使う）
$`\forall A\in |\cat{C}|.\, U(H(A)) = A`$
$`\forall A, B\in |\cat{C}|.\, H(A\otimes B) = H(A) \otimes H(B)`$ （モノイド積を厳密に保つ）
$`H(I) = I`$ （右辺の $`I`$ は規準的DSCFA）

$`H`$ は関手ではありませんが、モノイド圏の対象類 $`|\cat{C}|`$ と $`|\mrm{DSCFA}(\cat{C})|`$ が持つモノイド構造を保存する写像（モノイド準同型写像）になっています。

ダガー対称モノイド圏 $`\cat{C}`$ と、その上のハイパーグラフ構造 $`H:|\cat{C}| \to |\mrm{DSCFA}(\cat{C})|`$ を一緒にした $`(\cat{C}, H)`$ がダガー・ハイパーグラフ圏です。

なお、ダガー演算子を持たない対称モノイド圏 $`\cat{C}`$ に対しても、ハイパーグラフ構造は $`H:|\cat{C}| \to |\mrm{SCFA}(\cat{C})|`$ として定義できます。その場合 $`(\cat{C}, H)`$ はハイパーグラフ圏です。

$`\cat{C}`$ の対象 $`A`$ に対して、$`H(A)`$ の演算達は次のように書きます。

$`\quad \Delta_A, \bot_A, \nabla_A, \top_A`$

ダガー・ハイパーグラフ圏達の2-圏

$`F :\cat{C} \to \cat{D}`$ を、ダガー対称モノイド圏のあいだのダガー対称モノイド関手とします。$`(A, \Delta, \bot, \nabla, \top)`$ を、$`\cat{C}`$ 内のDSCFA〈ダガー特殊可換フロベニウス代数〉だとします。関手 $`F`$ で送った先 $`F(A)`$ を再びDSCFAにすることができます。

$`\quad (F(A), \Delta_{F(A)}, \bot_{F(A)}, \nabla_{F(A)}, \top_{F(A)}) \in |\mrm{DSCFA}(\cat{D})|`$

例えば、行った先の（$`\cat{D}`$ における）加法（可換モノイド演算）を定義するには、タイト・モノイド関手である $`F`$ の乗法ラクセイター $`\nu`$ と、もとの加法 $`\nabla = \nabla_A`$ を組み合わせます。

$`\nabla_{F(A)} : F(A)\otimes F(A) \to F(A) \In \cat{D}\\
\quad \nabla_{F(A)} := \nu_{A, A} ; F(\nabla_A)
`$

そのほかの演算達もうまく作ってあげると、台対象 $`F(A)`$ 上のDSCFA〈ダガー特殊可換フロベニウス代数〉が規準的に構成できます。そして、$`f:A \to B \In \cat{C}`$ がDSCFA準同型射なら、$`F(f): F(A) \to F(B ) \In \cat{D}`$ もDSCFA準同型射になります。

これはつまり、以下の図式が可換となるような対称モノイド関手 $`\mrm{DSCFA}(F)`$ が存在することです。

$`\begin{CD}
\mrm{DSCFA}(\cat{C}) @>{\mrm{DSCFA}(F)}>> \mrm{DSCFA}(\cat{D}) \\
@V{U}VV @VV{U}V\\
\cat{C} @>{F}>> \cat{D}
\end{CD}\\
\text{commutative in }{\bf SymMonCat}
`$

この誘導された関手 $`\mrm{DSCFA}(F)`$ を使って、ダガー・ハイパーグラフ関手の条件を記述できます。

$`(\cat{C}, H), (\cat{D}, H)`$ がダガー・ハイパーグラフ圏だとして、ダガー対称モノイド圏のあいだのダガー対称モノイド関手 $`F:\cat{C} \to \cat{D}`$ がダガー・ハイパーグラフ関手〈dagger hypergraph functor〉であるとは次の図式が可換になることです。

$`\begin{CD}
|\mrm{DSCFA}(\cat{C})| @>{\mrm{DSCFA}(F)}>> |\mrm{DSCFA}(\cat{D})| \\
@A{H}AA @AA{H}A\\
|\cat{C}| @>{F}>> |\cat{D}|
\end{CD}\\
\text{commutative in }{\bf Set}
`$

ダガー・ハイパーグラフ圏達を対象類とする2-圏 $`{\bf DagHypCat}`$ を定義できます。

$`{\bf DagHypCat}`$ の対象〈0-射〉は、小さなダガー・ハイパーグラフ圏
$`{\bf DagHypCat}`$ の射〈1-射〉は、ダガー・ハイパーグラフ圏のあいだのダガー・ハイパーグラフ関手
$`{\bf DagHypCat}`$ の2-射は、ダガー・ハイパーグラフ関手のあいだのモノイド自然変換

ドット付きワイヤリング図

冒頭で紹介したキッシンジャーの論文には、ダガー・ハイパーグラフ圏の射を表現するために便利な図が解説されています。キッシンジャーはその図をドット図〈dot diagram〉と呼んでますが、誤解されそうなので、ここではドット付きワイヤリング図〈dotted wiring diagram | wiring diagram with dots〉とします。

ドット付きワイヤリング図はストリング図の変種です。単に視覚的な説明のための道具というだけでなくて、それ自体を組み合わせ的構造として定義します。その組み合わせ的構造は、ハイパーグラフの親類だとみなせます。

ドット付きワイヤリング図の基本となるのは、次の記事で解説したポート／ボックス／ワイヤーからなるワイヤリング図です。

ワイヤリング図とケリー／マックレーン・グラフ

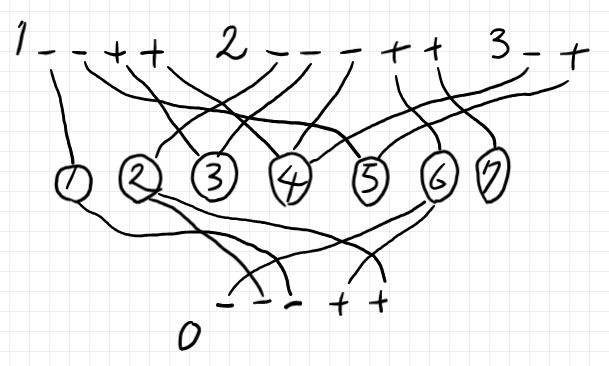
次はワイヤリング図の一例（上記記事から）です。

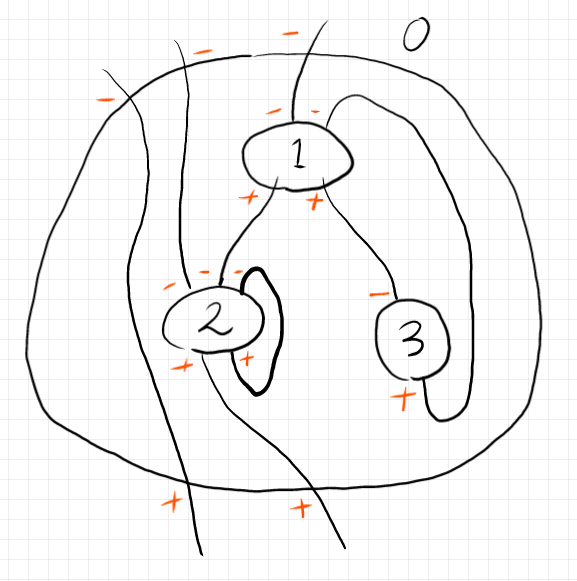
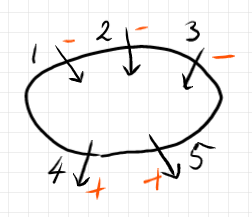
図のマル（ゆがんだ形もあるけど、気にしない）はノード〈node〉またはボックス〈box〉と呼びます。線がワイヤー〈wire〉です。ワイヤーがボックス境界と交わる点がポート〈port〉です。ポートには極性〈polarity〉と呼ばれる符号（プラスかマイナス）が付いています。上の図では、極性をオレンジ色で書き込んでいます。

極性の意味は、マイナスがボックスへの侵入〈吸い込み〉、プラスがボックスからの退出〈湧き出し〉と解釈します（下の図）。

一番外側のボックスは特別で、キャンバスボックス〈canvas box〉とか外部ボックス〈outer box〉と呼びます。ボックスを番号で識別するときは、特別な外部ボックスを0番とする約束です。外部ボックスでないボックスは内部ボックス〈inner box〉です。

外部ボックス〈キャンバスボックス〉と内部ボックスでは、ワイヤリングの際に守るべきルールが違います。

内部ボックスと内部ボックスをワイヤーで結ぶときは、プラスのポートとマイナスのポートを結ぶ。プラスからマイナスの向きと考える。
内部ボックスと外部ボックス（の境界）をワイヤーで結ぶときは、同じ極性（プラスどうし、マイナスどうし）を結ぶ。マイナスなら外部から侵入、プラスなら外部へ退出する向きと考える。
外部ボックス（の境界）のポートどうしをワイヤーで結ぶときは、プラスのポートとマイナスのポートを結ぶ。マイナスからプラスの向きと考える。

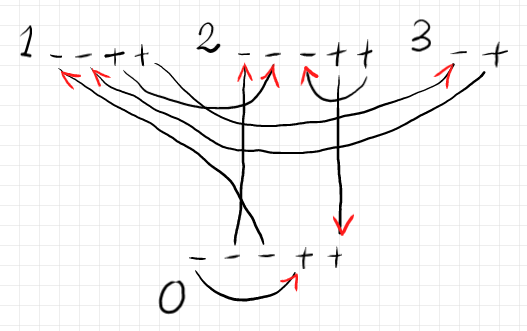
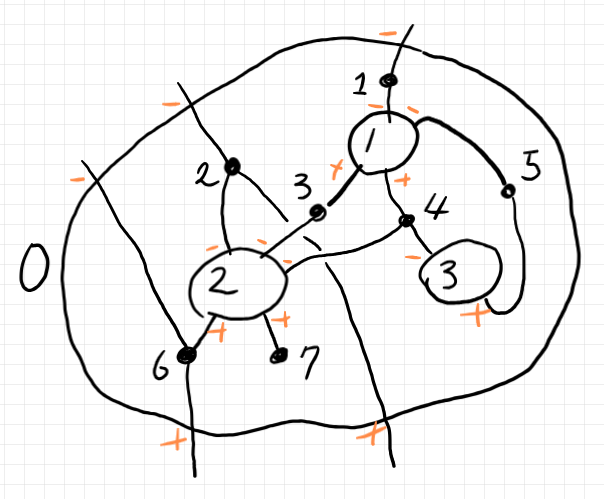
ワイヤリング図はケリー／マックレーン・グラフ〈Kelly-Mac Lane graph〉に翻訳できます。以下が上のワイヤリング図に対応するケリー／マックレーン・グラフです。

ボックスとポートでストリング図を表現する方法に興味があれば、次の記事を参照してください。

ストリング図のテキスト化：ボックス＆ポート方式

さて、ダガー・ハイパーグラフ圏の射を表現するためには、ワイヤリング図にドットという図要素を付け足します。ドットは黒丸で描きます。先にケリー／マックレーン・グラフで考えたほうが分かりやすいかも知れません。ケリー／マックレーン・グラフでは、（僕は、）内部ボックスを上段に、外部ノードを下段に配置しますが、中段にドットを配置することにします。

ドットはマル付き番号で示しました。ポートをワイヤーで結ぶ場合は、必ずドットを経由します。ポート間を直接ワイヤーで結ぶことはできません。

上記のケリー／マックレーン・グラフに対応するドット付きワイヤリング図は次のようになります。ドットは実際に黒丸で描いています。

ハイパーグラフとの関係

ドット付きワイヤリング図を、純粋に抽象的組み合わせ構造として定義する方法と、ドット付きワイヤリング図をダガー・ハイパーグラフ圏の射として解釈する方法は後日として、ドット付きワイヤリング図とハイパーグラフとの関係を説明しておきます。

ハイパーグラフ〈hypergraph〉は、無向グラフの拡張です。通常の無向グラフの辺が2つの頂点を含むのに対して、任意個の頂点を持つ辺〈ハイパー辺〉も認めた組み合わせ的構造です。ハイパーグラフは、集合 $`V`$ と集合 $`E`$ の組 $`(V, E)`$ で、$`E \subseteq \mrm{Pow}(V)`$ なものです（$`\mrm{Pow}(\hyp)`$ はベキ集合）。$`V`$ が頂点〈vertex〉の集合で、$`E`$ がハイパー辺〈hyperedge〉の集合です。

少し一般化した構造として、$`(V, E, b)`$ の組として：