以下の2つの過去記事で半グラフ〈semi-graph〉を扱っています。
心づもりとしては、キッシンジャー〈Aleks Kissinger〉の抽象テンソルシステム〈abstract tensor system〉(本文内の[Kis13])や物理で出てくるテンソルネットワーク(物理的内容は全然わかりませんが)に対する絵図的〈pictorial | graphical | diagrammatic〉な表示として半グラフを使いたいのです。
ストリング図はその目的で使えますが、ストリング図は基本的に有向グラフです。場合により無向グラフが必要なのです。ストリング図の無向グラフ版として半グラフが使えます。この記事では、今後の使用のために、半グラフの定義をひとつに決めます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\newcommand{\B}{\partial } % boundary
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
\newcommand{\Where}{\Keyword{Where } }
%\newcommand{\Let}{\Keyword{Let } }
`$
内容:
- なぜ半グラフなのか?
- 半グラフの幾何的・位相的な定義
- 組み合わせ構造としての半グラフ
- ボックス、ポート、ワイヤー
- 様々なラベリング
- 極性付けとワイヤーの向き
- アンカリング
- ストリング図とテンソル
- 過去記事
なぜ半グラフなのか?
ソフトウェア構成、データベース、ベイズ確率などに関する“状況”を、ストリング図として視覚化しようとすると、ワイヤーの方向や並んだワイヤー達の順番が不明であったり、気にしたくないことがあります。このような場合、当該の“状況”をとりあえず無向グラフとして記述しておいて、後から方向や順番を考えるほうが楽です。あるいは、方向や順番を気にしないで扱えたら便利です。
このような目的(なんらかの“状況”の記述)で使う無向グラフでは、辺〈無向辺〉の両端に頂点があるとは限りません。片一方の端だけが頂点に接続していたり、両端ともに頂点には接続してないケースもあります。以下の図は「半グラフの様々な定義」でも言及したハックニー論文からのコピーです。
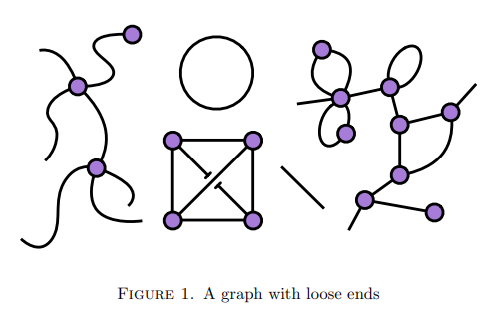
辺が途切れているように見えるところがありますが、下を通っていることを表しているだけで切れてはいません。この絵には次の5種類の辺〈edge〉がすべて現れています。
- 二頂点辺〈two-vertex edge〉 : 両端ともに頂点を持つ。
- 単頂点辺〈single-vertex edge〉 : 片一方だけ頂点を持つ。
- 無頂点辺〈vertexless edge〉 : 頂点を持たない。
- 自己ループ辺〈self-loop edge〉 : 1つの頂点を持つループ辺。
- 無頂点ループ〈vertexless loop〉 : 頂点を持たないループ辺。サークル〈circle〉とも呼ぶ。
二頂点辺(通常の無向辺)以外の辺も持つかも知れない無向グラフが半グラフ〈semi-graph〉です。
半グラフの幾何的・位相的な定義
「サークルを持つ半グラフ」の追記に書いたことですが、半グラフは幾何的・位相的に定義したほうが直感的にはむしろ簡単です。$`J`$ と $`S^1`$ を次のように定義します。
$`\quad J := \{x \in {\bf R} \mid 0 \lt x \lt 1 \}\\
\quad S^1 := \{ (x, y)\in {\bf R}^2 \mid x^2 + y^2 = 1 \}
`$
$`J, S^1`$ は単なる集合ではなくて、ユークリッド直線/平面としての $`{\bf R} / {\bf R}^2`$ の位相から受け継いだ位相を持つ位相空間と考えます。
位相空間 $`X`$ と有限部分集合 $`V \subseteq X`$ の組 $`(X, V)`$ が半グラフ*1であるとは次のことです。
- $`X`$ から $`V`$ を取り除いた位相空間 $`X\setminus V`$ は、幾つかの $`J`$ と幾つかの $`S^1`$ の直和空間と同相になる。
$`V`$ は頂点〈vertex〉の集合です。「幾つか」の個数を $`n, m`$ とすると、次の(位相空間としての)同型があります。
$`\quad (X \setminus V) \cong n\cdot J + m\cdot S^1\\
\Where \\
\quad n\cdot J = J + \cdots + J \: (n \text{個の直和})\\
\quad m\cdot S^1 = S^1 + \cdots + S^1 \: (m \text{個の直和})
`$
$`X \setminus V`$ の連結成分(直和成分と言っても同じ)を辺〈edge〉と呼び、$`\mrm{Edge}(X, V)`$ と書くことにします。$`e \in \mrm{Edge}(X, V)`$ のとき、$`e \subseteq X`$ と考えて位相の意味の閉包を $`\overline{e} \subseteq X`$ とします。写像 $`\B`$ を以下のように定義します。$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。
$`\Subject \B : \mrm{Edge}(X, V) \to \mrm{Pow}(V)\\
\For e \in \mrm{Edge}(X, V)\\
\Define \B(e) := \overline{e} \setminus e
`$
$`\B`$ を境界写像〈boundary map〉と呼びます。$`\overline{e} \setminus e`$ が $`V`$ の部分集合(ベキ集合 $`\mrm{Pow}(V)`$ の要素)になることは自明ではありません、確認する必要があります。$`e \cong S^1`$ なら $`\B(e) = \emptyset`$ です。$`e \cong J`$ の場合は、$`\B(e)`$ が空集合/一点だけ/ニ点の場合があります。
サークル($`S^1`$ と同型な辺)を持たない半グラフを無サークル半グラフ〈circleless semi-graph〉と呼びます。ここから先で扱う半グラフは有限な無サークル半グラフです。
組み合わせ構造としての半グラフ
有限な無サークル半グラフを組み合わせ的に定義しましょう。「半グラフの様々な定義」で述べたように色々な方法があります。ここでは、望月の方法とジョイアル/コック〈André Joyal, Joachim Kock〉の方法を混ぜた方法で定義します。
半グラフの辺を、真ん中(気持ち)でチョキンと切ります。1本の辺が2本の半辺〈half edge〉に分割されます。半辺の呼び名は他にも色々あります。
- 枝〈branch〉
- フラグ〈flag〉
- ダート〈dart〉
以下の半グラフ(「半グラフの様々な定義」から再掲)は5本の辺を持ちます。
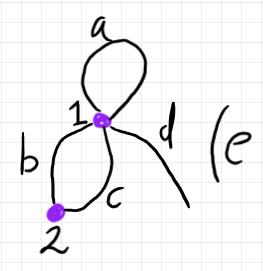
辺を半辺に切り分けると、10本の半辺ができます。
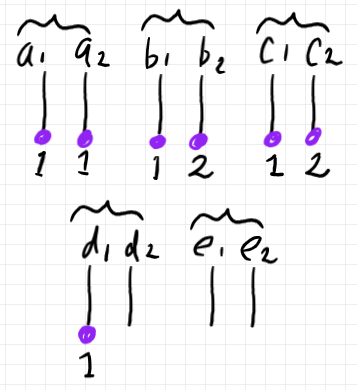
半グラフのすべての半辺の集合を $`H`$ 、頂点の集合を $`V`$ とします。半辺の境界となる頂点は1個か0個(無い)かのどちらかです。よって、半辺に対する境界写像は次のように定義できます。
$`\quad \B : H \to V + \{\bot\}`$
$`\bot`$ は境界頂点が無いことを表す特殊な値です。
半辺はもともとは辺だったので、パートナーがいます。半辺にパートナーである半辺を対応させる写像を $`p`$ とします。$`p`$ はパートナー指定対合〈partner designation involution〉です。
$`\quad p : H \to H\\
\quad p; p = \id_H
`$
$`p; p = \id_H`$ が対合〈involution〉の条件です。さらに、対合 $`p`$ は不動点を持ちません。
$`\quad \forall h \in H.\, p(h) \ne h`$
以上の構成素達で、半グラフの組み合わせ的構造を記述できます。もう一度構成素を列挙すると:
- 半辺の集合 $`H`$
- 頂点の集合 $`V`$
- 境界写像 $`\B :H \to V + \{\bot\}`$
- パートナー指定対合 $`p: H \to H`$
構成素をひとつの図式で描けば:
$`\quad\xymatrix{
% @(inDir, outDir)
H \ar@(ul, dl)[0,0]_{p}
\ar[r]^-{\B}
& {V + \{\bot\} }
}\\
\quad \text{ in } {\bf FinSet}
`$
ボックス、ポート、ワイヤー
前節の半グラフを表す図式を次のように書き換えます。変化したのは名前だけで、内容的には一切変わっていません。
$`\quad \xymatrix{
% @(inDir, outDir)
P \ar@(ul, dl)[0,0]_{w}
\ar[r]^-{b}
& {B + \{ b_0 \} }
}\\
\quad \text{ in } {\bf FinSet}
`$
半グラフの構成素である集合の要素の呼び名も変えます。
- 半辺をポート〈port〉と呼び替える。
- 頂点をボックス〈box〉と呼び替える。
- 境界写像を所属写像〈belonging map〉と呼び替える。
- パートナー指定対合をワイヤリング{対合 | 関数 | 写像}〈wiring {involution | function | map}〉と呼び替える。
- 辺をワイヤー〈wire〉と呼び替える。
呼び名を変えたところで、抽象的な組み合わせ構造としては同じなので、半グラフに対する抽象的議論に何の影響もありません。しかし、具体的描画法は変えます。先に例に出した半グラフは次のように描きます。

描き方の要点は:
- ボックスは大きさと境界を持つ図形(丸、四角、三角など)で描く。
- ポートは、ワイヤーがボックスに繋がる場所として描く。上の図では赤い点。
- 全体を囲むボックスを用意して、単頂点辺、無頂点辺に対応するワイヤーは“全体を囲むボックス”に接続するように描く。
“全体を囲むボックス”は、先の図式の $`b_0`$ に相当します。$`b_0`$ をキャンバスボックス〈canvas box〉または外部ボックス〈outer box〉と呼ぶことにします。ひとつの半グラフにキャンバスボックスは常にひとつだけ在ります。ボックスを番号で識別するときは、キャンバスボックスを0番とすることにしましょう(単なるコンベンション)。
ボックス、ポート、ワイヤーを使った図の描き方は次の2つの記事で詳しく説明しています。ただし、過去記事ではワイヤーに向きが付いた有向半グラフ〈ストリング図 | ワイヤリング図〉を扱っています*2。
キャンバスボックス $`b_0`$ も含めたボックスの集合を改めて $`B`$ として、キャンバスボックスをポインティングする写像を改めて $`b_0`$ とすると、半グラフの構造は次のように書けます。
$`\quad \xymatrix{
{} & {\bf 1} \ar[d]^{b_0}
\\
% @(inDir, outDir)
P \ar@(ul, dl)[0,0]_{w}
\ar[r]^-{b}
& B
}\\
\quad \text{ in } {\bf FinSet}
`$
ポートの集合 $`P`$ に次の同値関係を入れます。
$`\For x, y \in P\\
\Define x \sim y :\Iff x = w(y)
`$
この同値関係による商集合 $`P/\!\sim`$ はワイヤーの集合と考えることができます。図式にワイヤーの集合も書き加えると次のようになります。
$`\quad \xymatrix{
{} & {\bf 1} \ar[d]^{b_0}
\\
% @(inDir, outDir)
P \ar@(ul, dl)[0,0]_{w}
\ar[r]^-{b}
\ar[d]^{\pi}
& B
\\
{W = P/\!\sim}
& {}
}\\
\quad \text{ in } {\bf FinSet}
`$
ワイヤーの集合はいつでも再現できるので定義に含める必要はありません。が、ポートの集合、ボックスの集合、ワイヤーの集合を半グラフの構成素と考えると便利です。
様々なラベリング
半グラフのポート/ボックス/ワイヤーになんらかの値を対応させる写像〈関数〉をラベリング〈labeling〉と呼びます。値の集合を $`Y`$ として:
$`\quad f: P \to Y\\
\quad g: B \to Y\\
\quad h: W \to Y
`$
$`f`$ の形のラベリングはポートラベリング〈port labeling〉、$`g`$ ならボックスラベリング〈box labeling〉、$`h`$ ならワイヤーラベリング〈wire labeling〉です。
半グラフを実際に使う場面では、様々なラベリングが登場します。複数のラベリングが互いに絡み合ったりもします。ラベリングの多様さで混乱してしまうことが多々あり、半グラフを扱う上での鬼門と言っていいでしょう。
「ストリング図のテキスト化: ボックス&ポート方式」では次のように書いています。
意味的な情報を提供するラベルをセマンティックラベル〈semantic label〉、識別用のラベルは識別ラベル〈identification label〉と呼び区別することにします。
ここでも、セマンティック〈意味論的〉ラベリング〈semantic labeling〉と識別ラベリング〈identification labeling〉は区別します。その他に、主にテンソル計算のためのテキスト化で使うインデックス〈添字〉ラベリング〈index labeling〉を考えます。
インデックスラベリングが特にややこしくて、誤解と混乱の原因になります。これは、伝統的・古典的なテンソル記法におけるインデックス〈添字〉の名前を与えるポートラベリングです。おおよそのルールは:
- ワイヤーで繋がっているポートには原則的に同じインデックス名を割り当てる。
- しかし、クロネッカーのデルタを使うときは異なるインデックス名を割り当てる。
- ワイヤーで繋がっていないポートに同じ名前を与えてはいけない。
- インデックス名は便宜的なものなので、上のルールに反しない限り自由にリネームしてよい。
例えば、先ほどの例にインデックスラベリング(の一例)をすると以下の図のようになります。赤の英字小文字がインデックスラベルです。ワイヤーの両端が同じインデックスラベルのときは省略しています。赤の英字大文字はボックスのラベル(セマンティックラベルか識別ラベルかは場合による)です。
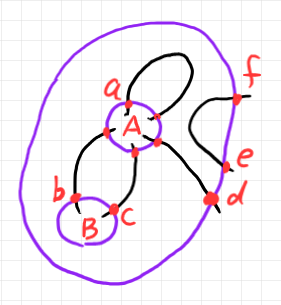
上記のラベリングのもとで、この半グラフをテキスト化すると次のようです。
$`\quad \left( \sum_{b, c}( (\sum_a A_{a\,a\, d\, c\, b}) B_{b\, c} )\right) \delta_{e\, f}
`$
インデックス〈添字〉を上下に振り分ける記法は使ってません(半グラフは無向なので)。
同じ構造を、データベースのテーブル達だと解釈したいなら、次のようなレイアウトで描くかも知れません。具体的な描画法の選択は、抽象的組み合わせ的な構造や議論に影響を与えません。

極性付けとワイヤーの向き
プラス記号とマイナス記号からなる二元集合 $`\{+, -\}`$ を考えて、この集合へのポートラベリングを極性付け〈polarization | 分極 | 偏極〉と呼びます。この場合、プラスとマイナスを極性〈polarity〉と呼びます。
半グラフに極性付けが与えられて、ワイヤーの両端が違う極性なら、そのワイヤーに向き〈direction〉を与えることができます。向きを電流の向き(プラスからマイナス)にするか、電子が動く向き(マイナスからプラス)にするかは悩むところです。どっちでもいいけど、決める必要があります。また、キャンバスボックスのポートは例外的に扱う必要があります。
ポートに付けられた極性から向きを決める話は次の記事に書いています。
上記過去記事から極性付き半グラフ〈polarized semi-graph〉と対応するケリー/マックレーン・グラフ〈Kelly-Mac Lane graph〉の絵を再掲します。
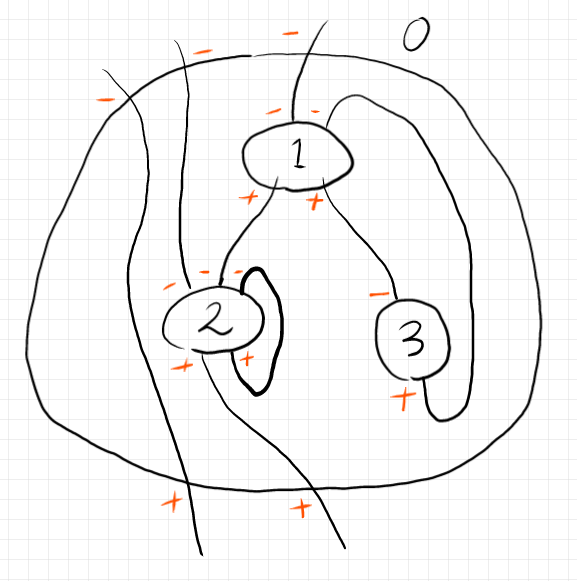
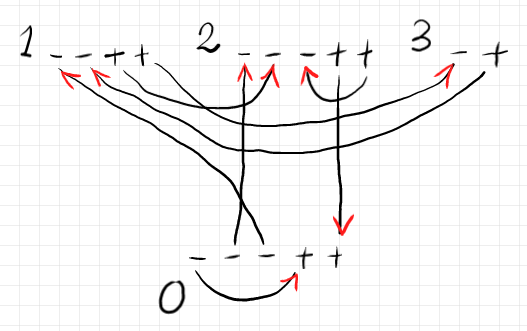
半グラフに与えられた任意の極性付け $`f: P \to \{+, -\}`$ がワイヤーの向きを決めるわけではありません。ワイヤーの両端が同じ極性なら向き付け不可能です。そのような極性付けも禁止しません。
半グラフの極性付けにより、次の3種のワイヤーが生じます。
- 有向ワイヤー〈directed wire〉 : 向きが決まったワイヤー
- 両端がプラスの不可向ワイヤー〈undirectable wire〉 : 向きは決まらない
- 両端がマイナスの不可向ワイヤー : 向きは決まらない
極性付けがない状態の無向ワイヤー〈undirected wire〉と不可向ワイヤーは区別します。
アンカリング
半グラフに対するアンカリング〈anchoring〉とは、ボックスのポート達に順序を与えることです。半グラフのテキスト化、解釈〈意味付け〉、計算では、ポート間の順序が必要になります。
ペンローズの絵図記法(1970年代)に圏論的定式化を与えたジョイアル/ストリートの歴史的論文[JS91](下)において、既にアンカリングに言及されています。
- [JS91]
- Title: The Geometry of Tensor Calculus, I
- Authors: ANDRE JOYAL, Ross STREET
- Year: 1991
- Pages: 58p
- URL: https://core.ac.uk/download/pdf/82659437.pdf
ここでは、アンカリングを3種類定義します。
- Aアンカリング〈A-anchoring〉: 各ボックスごとに、すべてのポートに全順序〈total order | 線形順序〉を与える。A は all ports から。
- Bアンカリング〈B-anchoring〉: 各ボックスごとに、ポート達を2つの部分に分けて、それぞれに全順序を与える。B は bipartite〈二部〉から。
- Cアンカリング〈C-anchoring〉: 各ボックスごとに、すべてのポートにサイクリック順序〈cyclic order〉を与える。C は cyclic から。
Cアンカリングのサイクリック順序は
$`\quad 0 \lt 1 \lt 2 \lt 0 \lt \cdots`$
のような順序です。正確には順序ではありませんが、習慣的に「順序」と呼んでいます。Cアンカリングが与えられたグラフをファットグラフ〈fat graph〉と呼ぶことがありますが、ファットグラフ = リボングラフ という用法のほうが多そうです(詳細は省略)。
[JS91] のアンカリングはBアンカリングです。Bアンカリングにおける「ポート達を2つの部分に分ける」ことは、極性付けと同じことです。よって、半グラフにBアンカリングすることは、次の手順で実行できます。
- 極性付けを行う。すべてのポートにプラスまたはマイナスの極性を割り当てる。
- ボックスごとに、プラスのポート達に全順序を与える。マイナスのポート達にも全順序を与える。
ここでは任意の極性付けを許しているので、Bアンカリングをしたからといって、すべてのワイヤーが向き付けられるとは限りません。うまいこと向き付けられたとしても、サイクルがないことは保証されません。
アンカリングを備えた半グラフをxアンカー付き半グラフ〈x-anchored semi-graph〉と呼びます。ここで、x は A, B, C のどれかです。Bアンカリングをよく使うので、単にアンカー付き半グラフと言ったら、それはBアンカー付き半グラフです。Bアンカー付き半グラフは極性付き半グラフであることに注意してください。
ストリング図とテンソル
半グラフにアンカリング〈Bアンカリング〉して、ワイヤーがうまいこと向き付けされた状況を考えましょう。内部ボックス〈inner box〉(キャンバスボックス以外のボックス)のあいだでは、ワイヤーの向きはプラスポートからマイナスポートの方向です。キャンバスボックスが絡むと違う向き付け規則になります(詳細は「ワイヤリング図とケリー/マックレーン・グラフ」参照)。このとき半グラフは有向半グラフとなり、これはすなわちストリング図〈string diagram〉です。キャンバスボックスは、外部環境とのインターフェイスを与えます。
ストリング図〈有向半グラフ〉では、各ボックスごとに入力ポートの集合/出力ポートの集合(空かも知れないが)が決まります。Bアンカリングにより、ポートのあいだの順番も決まります。例えば、$`A`$ とラベルされたボックスに次のようなインデックスラベリングができます。

小文字英字がインデックスラベルです。インデックスラベルが決まれば、伝統的・古典的テンソル記法によるテキスト化が可能になります。上記ボックスは次のように書けます。
$`\quad A_{a\, b\, c}^{x\, y}`$
伝統的・古典的テンソル記法の習慣では、入力ポートが下付きインデックス、出力ポートが上付きインデックスです。もし、$`y`$ と $`c`$ を自己ループで繋いだとしたら、それは次の記法で表現します。
$`\quad A_{a\, b\, t}^{x\, t}`$
ここで、上下に同じインデックス〈添字〉が登場したら和をとるというアインシュタインの総和規約〈Einstein summation convention〉を使っています。明示的に総和記号を書くなら:
$`\quad \sum_{t} A_{a\, b\, t}^{x\, t}`$
このような、ストリング図の描画・変形と対応する記号的な操作に対して、圏論的意味論をどう組み立てるかについては次の論文が示唆的です。
- [Kis13]
- Title: Abstract Tensor Systems as Monoidal Categories
- Author: Aleks Kissinger
- Submitted: 16 Aug 2013
- Pages: 19p
- URL: https://arxiv.org/abs/1308.3586
過去記事
ストリング図に関しては、このブログ内に相当量の記事があります。
幾つか選んでリストしておきます。その記事で使われていた絵も添えます。
- DI(依存性注入)からどこへ行こうか その1 (2006年)
- DI(依存性注入)からどこへ行こうか その2 (2006年)
ソフトウェアコンポネントを依存性注入で繋ぐ話です。
- ポートベース・コンポネント:ケーススタディ (2006年)
これもソフトウェアコンポネントを繋ぐ話。
- Webサービスの設計:Webの状態遷移図の描き方 (2010年)
Webサービス(サーバー側アプリケーション)の状態遷移図をストリング図っぽく描いてみる。
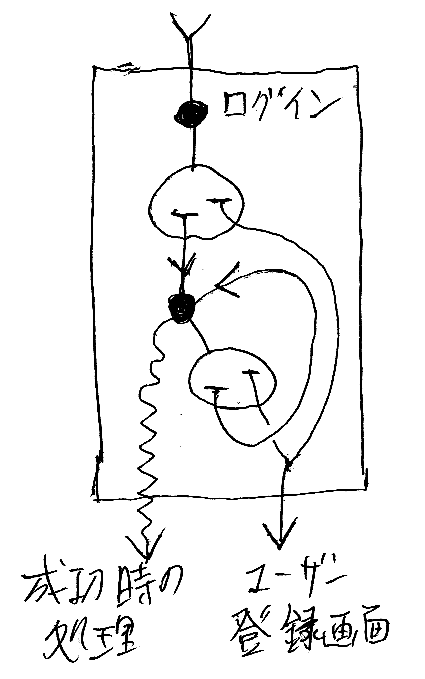
ストリング図に“穴”を考えてテンプレート計算をする。
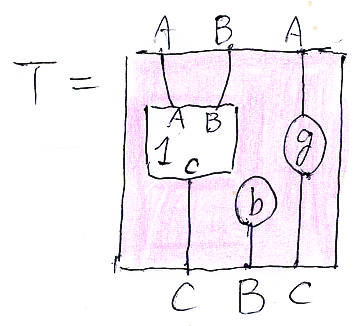
- アレンジメント計算 1: 確率グラフィカルモデル (2020年)
確率的な状況をストリング図で記述する話です。
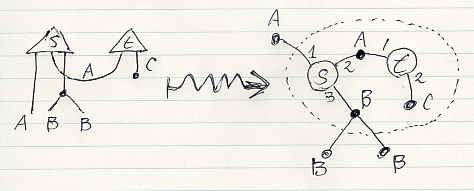
- 証明と計算は同じこと: 形式証明におけるノードとコネクター (2023年)
証明図もストリング図で。
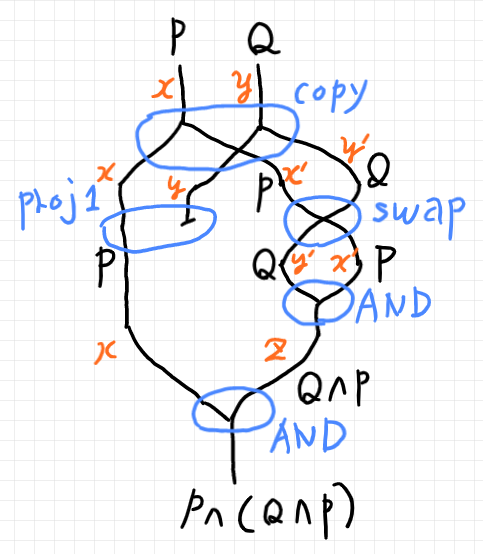
- バードトラック -- 群論的なファインマン図 (2010年)
絵図言語の簡単な歴史と絵図的表現のエグい事例を紹介。
*1:この記事では、有限な半グラフを考えます。
*2:[追記]「ダガー・ハイパーグラフ圏とドット付きワイヤリング図」も参考になるかも知れません。[/追記]