「テレオロジー圏の公理の自然な解釈」にて:
[テレオロジー圏に関する] このような事実を、スッキリと短く書く記述方法はないものでしょうか? ロマン〈Mario Roman〉のストリング図は確かに便利ですが、大規模高次な代数系を直接的に表現する記法・描画法が欲しいところです。
ヘッジーズ/ロマン〈Jules Hedges, Mario Roman〉のテレオロジー圏に対して直截的で正確な記述を試みてみましょう。テレオロジー圏を大規模高次な代数系〈large-sized higher algebra〉と捉えて定式化します。台〈underlying stuff〉となるコンストラクタ系(「コンストラクタ系と変換手性」参照)に対して、自然性や対角自然性の条件を付け足していきます。
「テレオロジー圏の公理の自然な解釈」で述べた内容を納得するための基盤の部分を確認するのがこの記事の目的です。$`\newcommand{\whitestar}{\unicode{x2606}}
\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\ol}[1]{\overline{#1} }
\newcommand{\ul}[1]{\underline{#1} }
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in }}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\ract}{\mathop{\bullet} }
\newcommand{\J}{\mathrm{J} }
\newcommand{\lto}[1]{\overset{#1}{\longrightarrow} }
\newcommand{\ltwoto}[1]{\overset{#1}{\Longrightarrow} }
\newcommand{\plto}[1]{\supseteq\!\overset{#1}{\longrightarrow} }
\newcommand{\WCAT}{\widehat{\bf CAT} }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%\newcommand{\Where}{\Keyword{Where } }
\newcommand{\Notation}{\Keyword{Notation } }
%`$
内容:
無法則変換と無法則対角変換
代数系は、台となるナニカに等式的法則を課すことで定義されます。テレオロジー圏のような大規模高次な代数系でも同じ定義方法を採用したいのですが、台となるナニカに名前がないので記述に難儀します。
法則を課す前のナニカを表すために「非関手的」「非自然」のような形容詞を使っていました。実は、自己関手のランベック代数とモナドのアイレンベルク/ムーア代数に関しても同様な悩みがあったのですが、最近は「有法則〈lawful〉」と「無法則〈lawless〉」という形容詞を使っています。これはレンズに対して使われていた形容詞ですがとても便利な言葉です(「有法則代数と無法則代数」参照)。
圏の2-圏 $`{\bf CAT}`$ の射〈k-射〉には次のものがあります。
- 0-射〈対象〉は圏
- 1-射〈射〉は関手〈(1, 0)-変換手〉
- 2-射は自然変換〈(1, 1)-変換手〉
2-射である自然変換のプロファイルは次のように書けます。
$`\quad \alpha :: F \twoto G : \cat{C} \to \cat{D} \In {\bf CAT}`$
これに対して自然性という法則を満たさない(正確には、自然性には言及しない)無法則変換〈lawless transformation〉を次のように書くことにします。
$`\quad \xi :: S \ltwoto{0} T : \cat{C} \lto{0} \cat{D} \In \WCAT`$
この意味は以下のとおりです。出てくる記号は「コンストラクタ系と変換手性」を参照してください。
- $`\xi : \cat{C} \lto{0, +} \cat{D} \In \WCAT`$
- $`S : \cat{C} \lto{0} \cat{D} \In \WCAT`$
- $`T : \cat{C} \lto{0} \cat{D} \In \WCAT`$
- $`\xi ; \mrm{dom}_{\cat{D}} = S \In {\bf SET}`$
- $`\xi ; \mrm{com}_{\cat{D}} = T \In {\bf SET}`$
$`\mrm{dom}_{\cat{D}}, \mrm{cod}_{\cat{D}}`$ は、圏 $`\cat{D}`$ の構造の一部である写像です。$`\WCAT`$ は、無法則だろうが何だろうがかまわずに寄せ集めた圏的構造物〈category-like structure〉です*1。$`\WCAT`$ が正体不明で気持ち悪いなら、$`{\bf SET}`$ のなかでの記述にできます。
- $`\xi : |\cat{C}|_0 \to |\cat{D}|_1 \In {\bf SET}`$
- $`S : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`T : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`\xi ; \mrm{dom}_{\cat{D}} = S : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`\xi ; \mrm{com}_{\cat{D}} = T : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
次の点には注意してください。
- 無法則変換の両端は、関手ではなく 0-to-0 コンストラクタなので、自然性を定義するすべがない。
- 無法則変換の両端が、関手の対象パートであったとしても、自然性〈法則〉は要求してない。
無法則変換という概念を認めれば、2つの関手(関手性を満たすコンストラクタ系として定義される) $`F, G`$ と無法則変換
$`\quad \xi:: F_0 \ltwoto{0} G_0 :\cat{C} \lto{0} \cat{D}`$
をまずは提示して、後から関手性を要求する形の記述ができます。
無法則変換と同様に、“対角自然性を除いた対角自然変換”(日本語はおかしい)として無法則対角変換〈lawless ditransformation〉を定義します。$`\tau`$ が無法則対角変換であることを次のように書きます。
$`\quad \tau :: V \ltwoto{0\,\bullet} W : \cat{C}\times\cat{C}^\op \lto{0} \cat{D} \In \WCAT`$
この意味を(大きい)集合圏で記述すれば次のようです。
- $`\tau : |\cat{C}|_0 \to |\cat{D}|_1 \In {\bf SET}`$
- $`V : |\cat{C}\times \cat{C}^\op|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`W : |\cat{C}\times \cat{C}^\op|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`\tau ; \mrm{dom}_{\cat{D}} = \Delta_{|\cat{C}|_0} ; V : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`\tau ; \mrm{com}_{\cat{D}} = \Delta_{|\cat{C}|_0} ; W : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
$`\Delta_{|\cat{C}|_0}`$ は対象集合の対角写像〈コピー写像〉ですが、
$`\quad |\cat{D}|_0 = |\cat{C}\times \cat{C}^\op|_0 \cong |\cat{C}|_0\times |\cat{C}^\op|_0 \cong |\cat{C}|_0\times |\cat{C}|_0`$
であることを利用して、プロファイルを $`|\cat{C}|_0 \to |\cat{D}|_0 = |\cat{C}\times \cat{C}^\op|_0`$ とみなしています。確かに、$`\cat{C}\times\cat{C}^\op`$ の対象対角線部分で定義された射の族です。
2つの関手と無法則対角自然変換が与えられた状況で、その変換が対角自然性〈dinaturality〉を持つという主張は意味を持ちます。
いずれにしても、法則を明示的に述べたいときは、その台となる無法則なモノ〈underlying lawless stuff〉が必要なのです。
アクテゴリー構造
テレオロジー圏の主役は同語反復射の族〈family of tautological morphisms〉ですが、主役をささえる脇役達がいます。この脇役達は、アクテゴリー構造〈加群構造〉から派生するものです。脇役がいないと主役が成立し得ないことから、テレオロジー圏にとってアクテゴリー構造が本質的であることがわかります。
通常、アクテゴリー作用は左作用を採用します。が、右作用のほうがストリング図との相性がいいので、ここでは右作用を使います。左でも右でも本質的な差はないです。
$`\cat{M} = (\cat{M}, \otimes, I)`$ (記号の乱用/詳細省略)をモノイド圏として、右アクテゴリーを $`(\cat{M}, \cat{C}, \ract)`$ のように書きます。これも記号の乱用/詳細省略の書き方です。が、事情をハッキリさせておかないと誤認・誤解につながるので、いくつか補足・注意をしておきます。
- $`(\cat{M}, \otimes, I)`$ を詳しく書けば、$`(\cat{M}, \otimes, I, \alpha, \lambda,\rho)`$ で、$`\alpha, \lambda,\rho`$ はそれぞれ結合律子〈associator〉、左単位律子〈left unitor〉、右単位律子〈right unitor〉です。
- 二項関手 $`(\ract)`$ を $`R`$ とも書きます。'R' は Right からで、右作用であることを強調しています。
- $`(\cat{M}, \cat{C}, \ract)`$ を詳しく書けば、$`(\cat{M}, \cat{C}, R, \alpha, \rho)`$ で、$`\alpha, \rho`$ は右作用に関する結合律子〈associator〉と右単位律子〈right unitor〉です。モノイド積と右作用で、律子〈法則射〉の名前をオーバーロードしているので注意。
アクテゴリーの右作用 $`R:\cat{C}\times \cat{M} \to \cat{C}`$ は次の2つの形に拡張できます。
- $`S : (\cat{C}\times \cat{C}^\op) \times (\cat{M}\times\cat{M}^\op) \to (\cat{C}\times \cat{C}^\op) \In {\bf CAT}`$
- $`T : (\cat{C}\times \cat{C}^\op) \times \cat{M} \to (\cat{C}\times \cat{C}^\op) \In {\bf CAT}`$
$`R, S, T`$ は単にアルファベット順で文字を選んだだけです。二項演算子記号としては、$`S`$ には '$`\ract`$' をオーバーロードし、$`T`$ は '$`\odot`$' を使います(記号の選び方やオーバーロードの程度は好みの問題です)。
$`\For [A, A'] \in |\cat{C}\times \cat{C}^\op|\\
\For [M, M'] \in |\cat{M}\times \cat{M}^\op|\\
\quad S([A, A'], [M, M']) = [A, A'] \ract [M, M'] := [A\ract M, A'\ract M']\\
\:\\
\For [A, A'] \in |\cat{C}\times \cat{C}^\op|\\
\For M \in |\cat{M}|\\
\quad T([A, A'],M) = [A, A'] \odot M := [A\ract M, A'\ract M]
`$
射に関しても同様に定義します。ただし、反対圏が絡んでいるので注意が必要です。$`\Delta'_{\cat{M}}`$ を射を次のようにコピーするひねり対角関手〈twisted diagonal functor〉だとします。
$`\quad (f:M \to X \In \cat{M}) \mapsto ([f:M \to X, f:M \leftarrow X] \In \cat{M}\times \cat{M}^\op)`$
$`\Delta'_{\cat{M}}`$ を使って、$`S, T`$ の関係は次のように書けます。
$`\require{AMScd}
\begin{CD}
(\cat{C}\times \cat{C}^\op)\times \cat{M} @>{T = (\odot)}>> (\cat{C}\times \cat{C}^\op)\\
@V{\mrm{Id}_{\cat{C}\times \cat{C}^\op} \times \Delta'_{\cat{M}}}VV @|\\
(\cat{C}\times \cat{C}^\op)\times (\cat{M}\times \cat{M}^\op) @>{S = (\ract)}>> (\cat{C}\times \cat{C}^\op)
\end{CD}\\
\text{commutative in }{\bf CAT}`$
さらに注意すべきは、$`S, T`$ に伴う結合律子/右単位律子を構成する必要があり、それらがマックレーンの五角形法則/三角形法則を満たすことの確認も必要なことです。以下の過去記事を参照してください。
もとになる右アクテゴリーと、それから構成された右アクテゴリーは次のようになります。結合律子と右単位律子(の名前)はすべてオーバーロードします。
- $`(\cat{M}, \cat{C}, R, \alpha, \rho),\; R = (\ract)`$
- $`(\cat{M}\times \cat{M}^\op, \cat{C}\times \cat{C}^\op, S, \alpha, \rho),\; S = (\ract)`$
- $`(\cat{M}, \cat{C}\times \cat{C}^\op, T, \alpha, \rho),\; T = (\odot)`$
ラックス・モノイド関手と反ラックス・モノイド関手
圏の2-圏の1-圏部分は、直積に関してデカルト閉圏〈CCC〉の構造を持ちます。したがって、関手をカリー化/反カリー化できます。カリー化には以下の記法をつかいます。関手圏〈指数対象〉はブラケットで示します。$`(-)|_{\le 1}`$ は高次圏の1-圏部分を示しますが、あまり気にしなくてもいいです。
- 圏の2-圏の1-圏部分はデカルト閉圏
$`{\bf CAT}|_{\le 1} = ({\bf CAT}|_{\le 1}, \times, {\bf I}, [-,-]) \in |\mathbb{CCC}|`$ - 二項関手 $`F:\cat{C}\times \cat{D} \to \cat{E} \In {\bf CAT}|_{\le 1}`$
- その左カリー化(第一変数を指数化) $`{^\cap F}: \cat{D} \to [\cat{C}, \cat{E}] \In {\bf CAT}|_{\le 1}`$
- その右カリー化(第二変数を指数化) $`F^\cap: \cat{C} \to [\cat{D}, \cat{E}] \In {\bf CAT}|_{\le 1}`$
左右の指数を以下のように使い分けると、絵との対応がより分かりやすいですが、ここではブラケットにします。
- $`F:\cat{C}\times \cat{D} \to \cat{E} \In {\bf CAT}|_{\le 1}`$
- $`{^\cap F}: \cat{D} \to {^{\cat{C}} \cat{E}} \In {\bf CAT}|_{\le 1}`$
- $`F^\cap: \cat{C} \to , \cat{E}^{\cat{D}} \In {\bf CAT}|_{\le 1}`$
前節で出てきた右モノイド作用をカリー化すると、次のような“高階関手”が得られます。
- $`{^\cap R} : \cat{M} \to [\cat{C}, \cat{C}] \In {\bf CAT}|_{\le 1}`$
- $`{ S^\cap} : \cat{C}\times \cat{C}^\op \to [\cat{M} \times \cat{M}^\op, \cat{C}\times \cat{C}^\op] \In {\bf CAT}|_{\le 1}`$
- $`{^\cap T} : \cat{M} \to [\cat{C}\times \cat{C}^\op,\cat{C}\times \cat{C}^\op] \In {\bf CAT}|_{\le 1}`$
上記の“高階関手”達は単なる関手ですが、“モノイド積/右モノイド作用”の“結合律子/単位律子”を使うことによって、$`R, T`$ からはラックス・モノイド関手を構成できます -- 「モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形」を参照してください。
ラックス・モノイド関手の緩化子〈ラクセイター〉(「緩化子〈ラクセイター〉」参照)を $`\ol{\alpha}, \ol{\lambda}, \ol{\rho}`$ とします。$`\ol{\alpha}`$ が積〈乗法〉緩化子で、積の保存性を緩化します。$`\ol{\lambda}, \ol{\rho}`$ が左右の単位緩化子で、左右の単位の保存性を緩化します。文字が足りなくなるので、モノイド圏の律子に上線を引いた記号にしました。緩化子の記号は、出現するすべてのラックス・モノイド関手でオーバーロードします。
アクテゴリーの右作用から得られたラックス・モノイド関手をハッキリと記述すれば以下のようです。行き先のモノイド圏は、自己関手圏に結合(図式順二項演算子記号は '$`*`$')をモノイド積として入れた厳密モノイド圏です。
$`\quad ({^\cap R}, \ol{\alpha}, \ol{\lambda}, \ol{\rho})
: (\cat{M}, \otimes, I) \to ([\cat{C}, \cat{C}], *, \mrm{Id}_{\cat{C}}) \In {\bf MonCAT}^\mrm{lax}\\
\quad ({^\cap T}, \ol{\alpha}, \ol{\lambda}, \ol{\rho} )
: (\cat{M}, \otimes, I) \to ([\cat{C}\times \cat{C}^\op,\cat{C}\times \cat{C}^\op], *, \mrm{Id}_{\cat{C}\times \cat{C}^\op}) \In {\bf MonCAT}^\mrm{lax}
`$
上記のラックス・モノイド関手の緩化子達はすべて可逆〈自然同型〉なので、反ラックス・モノイド関手にもなります。反ラックス・モノイド関手の反緩化子〈反ラクセイター | oplaxator〉はモノイド圏の律子に下線を引いた記号にします。次のようです。
$`\quad ({^\cap R}, \ul{\alpha}, \ul{\lambda}, \ul{\rho})
: (\cat{M}, \otimes, I) \to ([\cat{C}, \cat{C}], *, \mrm{Id}_{\cat{C}}) \In {\bf MonCAT}^\mrm{oplax}\\
\quad ({^\cap T}, \ul{\alpha}, \ul{\lambda}, \ul{\rho} )
: (\cat{M}, \otimes, I) \to ([\cat{C}\times \cat{C}^\op,\cat{C}\times \cat{C}^\op], *, \mrm{Id}_{\cat{C}\times \cat{C}^\op}) \In {\bf MonCAT}^\mrm{oplax}
`$
「テレオロジー圏の公理の自然な解釈」で出した太字のアルファ $`\boldsymbol{\alpha}`$ は、反ラックス・モノイド関手としての $`{^\cap T}`$ の積〈乗法〉反緩化子 $`\ul{\alpha}`$ のことでした(左作用/右作用の違いはありますが)。
ラックス・モノイド関手/反ラックス・モノイド関手の記述と計算には、ストライプ図が便利に使えます。これについても「モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形」に書いてあります。ストライプ図とストリング図を組み合わせる話は次の過去記事などを見てください。
定数関手
記述を簡潔にするために、
$`\quad \cat{D} := \cat{C}\times \cat{C}^\op`$
と置きます。$`\cat{D}`$ は、$`\cat{C}`$ の対象・射の順行・逆行ペアの圏です。つまり、$`\cat{C}`$ を双方向化した圏であり、レンズ/オプティックなどの双方向変換の基礎となります。
$`\cat{D}`$ を使って、今まで出てきた関手をもう一度書き出すと:
- $`S = (\ract) : \cat{D} \times (\cat{M}\times\cat{M}^\op) \to \cat{D} \In {\bf CAT}`$
- $`S^\cap : \cat{D} \to [\cat{M}\times\cat{M}^\op, \cat{D}] \In {\bf CAT}`$
- $`T = (\odot) : \cat{D} \times \cat{M} \to \cat{D} \In {\bf CAT}`$
- $`{^\cap T} : \cat{M} \to [\cat{D}, \cat{D}] \In {\bf CAT}`$
これらの関手(カリー化/反カリー化を無視すれば、$`S, T`$ の2つ)以外に、テレオロジー圏の構成素として重要な役割を演じるのが定数関手です。
まずは関数に関して、定数関数を表す記法を導入します; 集合 $`X, Y`$ が了解されている状況で、$`{^! b}`$ という記号の意味は:
$`\For X, Y \in |{\bf Set}|\\
\For b\in Y\\
\quad {^! b} = \lambda\, x\in X. b
%`$
つまり、値が常に $`b`$ である定数関数です。同様な記法 $`{^! B}`$ を関手に対しても使います。
$`\For \cat{X}, \cat{Y} \in |{\bf CAT}|\\
\For B\in |\cat{Y}|\\
\quad {^! B} :=
\left\{
\begin{array}{l}
\lambda\, X\in |\cat{X}|. B \\
\lambda\, f\in \mrm{Mor}(\cat{X}). \id_B
\end{array}
\right.
%`$
対象に定数関手を対応させる関手もあります。
$`\For \cat{X}, \cat{Y} \in |{\bf CAT}|\\
\quad \mrm{K}_{\cat{X}, \cat{Y}} : \cat{X} \to [\cat{Y},\cat{X}] \In {\bf CAT}\\
\quad \mrm{K}_{\cat{X}, \cat{Y}} :=
\left\{
\begin{array}{l}
\lambda\, X\in |\cat{X}|.\, {^! X} \\
\lambda\, (f:X \to Y)\in \mrm{Mor}(\cat{X}).\, {^! f} :: {^! X}\twoto{^! Y}
\end{array}
\right.
`$
$`{^! f}`$ は定数関手のあいだを結ぶ自然変換です。
関手 $`K_{\cat{X}, \cat{Y}}`$ は直積の第一射影 $`\cat{X}\times\cat{Y} \to \cat{X}`$ を右カリー化した関手です。もちろん、第二射影を左カリー化しても同様な定義ができます。
同語反復射の族
いよいよ主役の登場、テレオロジー圏を構成する同語反復射の族 $`\varepsilon`$ です。$`\varepsilon`$ は次のようなコンストラクタ(「コンストラクタ系と変換手性」参照)です。
$`\quad \varepsilon : \cat{M}\times \cat{D} \lto{0, +} \cat{T} \In \WCAT`$
ここで、圏 $`\cat{T}`$ はテレオロジー圏の構成素のひとつです。
次のように書いても同じことです。
$`\quad \varepsilon : |\cat{M}|_0\times |\cat{C}|_0\times |\cat{C}^\op|_0 \to |\cat{T}|_1 \In {\bf SET}`$
この時点(公理に言及してない時点)では、$`\varepsilon`$ は無法則コンストラクタです。
無法則コンストラクタもカリー化できるので、左右のカリー化コンストラクタは次のようになります。
$`\quad \varepsilon^\cap : \cat{M} \lto{0} [\cat{D} \lto{0, +} \cat{T}] \In \WCAT\\
\quad {^\cap \varepsilon} : \cat{D} \lto{0} [\cat{M} \lto{0, +} \cat{T}] \In \WCAT
%`$
ここで、$`[\cat{D} \lto{0, +} \cat{T}]`$ などは単なる集合ですが、離散圏とみなします。次のようにも書けます。
$`\quad \varepsilon^\cap : |\cat{M}|_0 \to \mrm{MAP}(|\cat{C}|_0\times|\cat{C}^\op|_0, |\cat{T}|_1 )\In {\bf SET}\\
\quad {^\cap \varepsilon} : |\cat{C}|_0\times|\cat{C}^\op|_0 \to \mrm{MAP}(|\cat{M}|_0 \to |\cat{T}|_1 ) \In {\bf SET}
%`$
「テレオロジー圏の公理の自然な解釈」で次のように述べました。
まとめると、テレオロジー圏の $`\varepsilon^-_{[-,-]}`$ は次の性質を持ちます。
- 上付き添字を固定して自然変換
- 下付き添字を固定して対角自然変換
- 上付き添字はモノイド積と協調する
一番と三番は $`\varepsilon^\cap`$ に対して要求する性質、二番は $`{^\cap \varepsilon}`$ に対して要求する性質です。$`M\in|\cat{M}|, A\in |\cat{C}|, A'\in |\cat{C}^\op|`$ として:
- $`\varepsilon^\cap(M)`$ は自然性〈naturality〉を持つ。
- $`{^\cap \varepsilon}([A, A'])`$ は対角自然性〈dinaturality〉を持つ。
- $`\varepsilon^\cap`$ は、$`J`$ に対する左ラックス作用構造を与える。
自然性と対角自然性を主張するには、変換/対角変換の両端となる関手を指定する必要があります。左ラックス作用構造がいかなるものかも説明が必要です。
自然性と対角自然性
ナニカが自然性を持つというときは、事前に次をハッキリさせる必要があります。
- 自然性を持つナニカである 0-to-1 コンストラクタ
- 自然変換の両端(域と余域)となるべき2つの関手
テレオロジー圏の公理として、$`\varepsilon^\cap`$ が自然性を持つと主張したいので、両端の関手を明示しましょう。一時的に使う名前 $`\Phi, \Psi`$ を次のように定義します。
- $`\Phi := {^\cap T} * [\mrm{Id}_D, J] : \cat{M} \to [\cat{D}, \cat{T}] \In {\bf CAT}`$
- $`\Psi := {^! J} : \cat{M} \to [\cat{D}, \cat{T}] \In {\bf CAT}`$
ここで、$`J:\cat{C} \to \cat{T}`$ はテレオロジーの構成素である関手です。$`M\in |\cat{M}|`$ に対する値は次のようです。
- $`\Phi(M) = ({^cap T} * [\mrm{Id}_D, J])(M) = J(- \odot M)\;\in [\cat{D}, \cat{T}]`$
- $`\Psi(M) := ({^! J})(M) = J \; \in [\cat{D}, \cat{T}]`$
これらを使って、テレオロジー圏の公理(のひとつ)を述べることができます。
任意の $`M\in \cat{M}`$ に対して、
$`\quad \varepsilon^\cap(M):: \Phi(M)_0 \ltwoto{0} \Psi(M)_0 : \cat{D} \lto{0} \cat{T}\In\WCAT`$
は自然性を持つ。
ここで、
$`\quad\Phi(M) = (J(- \odot M) : \cat{D} \to \cat{T} \In {\bf CAT} )\\
\quad\Psi(M) = (J : \cat{D} \to \cat{T} \In {\bf CAT} )
`$
対角自然性の場合も同様に、事前に次をハッキリさせる必要があります。
- 対角自然性を持つナニカである 0-to-1 コンストラクタ
- 対角自然変換の両端(域と余域)となるべき2つの関手
一時的に使う名前 $`\Phi, \Psi`$ を新たに次のように定義します。
- $`\Phi := S^\cap * [\mrm{Id}_{\cat{M}\times\cat{M}^\op}, J] : \cat{D} \to [\cat{M}\times\cat{M}^\op, \cat{D}] \In {\bf CAT}`$
- $`\Psi := K_{\cat{D}, \cat{M}\times\cat{M}^\op} * [\mrm{Id}_{\cat{M}\times\cat{M}^\op}, J] : \cat{D} \to [\cat{M}\times\cat{M}^\op, \cat{D}] \In {\bf CAT}`$
$`[A, A']\in |\cat{D}|`$ に対する値は次のようです。
- $`\Phi([A, A']) = (S^\cap * [\mrm{Id}_D, J])([A, A']) = J([A\ract -, A'\ract -])\;\in [\cat{M}\times\cat{M}^\op, \cat{T}]`$
- $`\Psi([A, A']) = (K_{\cat{D}, \cat{M}\times\cat{M}^\op} * [\mrm{Id}_{\cat{M}\times\cat{M}^\op}, J])([A, A']) = {^! (J([A, A']) )}\;\in [\cat{M}\times\cat{M}^\op, \cat{T}]`$
これらを使って、もうひとつのテレオロジー圏の公理を述べることができます。
任意の $`[A, A']\in \cat{D}`$ に対して、
$`\quad {^\cap \varepsilon}([A, A']) :: \Phi([A, A'])_0 \ltwoto{0,\bullet} \Psi([A, A'])_0 : \cat{M}\times \cat{M}^\op \lto{0} \cat{T}\In \WCAT`$
は対角自然性を持つ。
ここで、
$`\quad\Phi([A, A']) = ( J([A\ract -, A'\ract -]) : \cat{M}\times\cat{M}^\op \to \cat{T} \In {\bf CAT} ) \\
\quad\Psi([A, A']) = ( {^! (J([A, A']) )} : \cat{M}\times\cat{M}^\op \to \cat{T} \In {\bf CAT} )
`$
左ラックス作用構造
適切な名前が見つからないので、とりあえず左ラックス作用構造と呼びます。「左」や「右」は恣意的な約束を基準にしているだけで、絶対的な意味はありません。関手の結合を左から右だとみなした場合に「左作用」に見えるってことです。
関手 $`J:\cat{D} \to \cat{T}`$ を固定したとき、任意の自己関手 $`F:\cat{D} \to \cat{D}`$ は関手の結合により $`J`$ に“左から作用”します。
$`\quad J \mapsto F* J`$
しかし、作用の結果はもはや $`J`$ とは限らないので、別な自己関手を続けて $`J`$ に左作用させるわけにはいきません。もし、次のような自然変換 $`\nu`$ があれば、$`F`$-左作用の結果を再び $`J`$ に戻すことができます。
$`\quad \nu::F*J \twoto J`$
このような $`\nu`$ を系統的に与えられれば、固定された $`J`$ への自己関手達の左作用が定義できるでしょう。
とはいえ、$`\mrm{End}(\cat{D})`$ 全体を左作用域にするのは無謀なので、左作用域はモノイド圏 $`\cat{M}`$ とします。アクテゴリーの右作用 $`T = (\odot):\cat{D}\times \cat{M} \to \cat{D}`$ を経由して、モノイド圏 $`\cat{M}`$ の $`J`$ への左作用を定義します。その左作用を $`\star`$ とすると:
$`\quad M \star J := {^\cap T}(M) * J`$
$`\varepsilon^M`$ は次のような自然変換になります。
$`\quad \varepsilon^M :: M \star J \twoto J`$
左作用 $`\star`$ と $`\varepsilon^M`$ 達が作る大規模高次代数系が、ある種の単位法則と結合法則を満たすことがテレオロジー圏のバニシング法則とバンドリング法則です。テキスト数式で記述することに息切れしてきたので、「テレオロジー圏の公理の自然な解釈 」に載せた2つの絵を再掲します。ただし、絵では $`T = (\odot)`$ が左作用になっています。
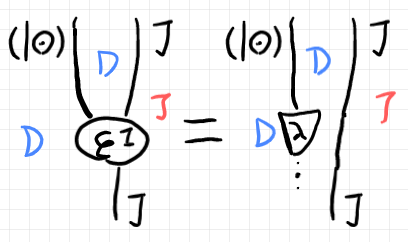
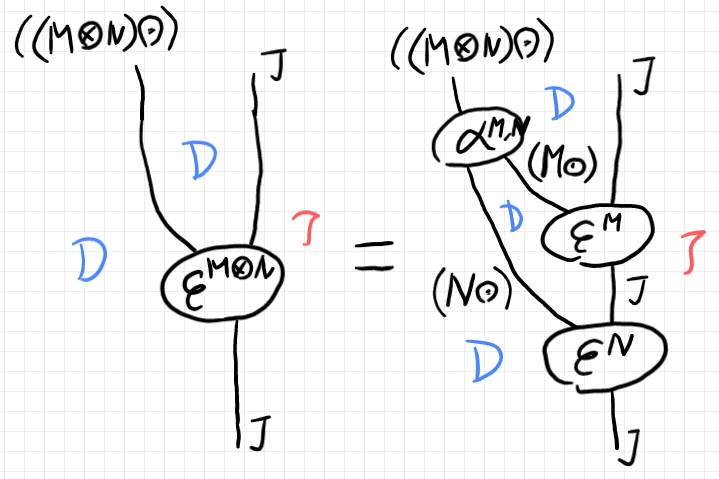
これらの大規模高次な法則を“インスタンス化”すると、圏 $`\cat{D} = \cat{C}\times\cat{C}^\op`$ 内の等式的法則が得られます。その等式をまたストリング図等式として描くことができます -- それが我々がよく目にしている法則記述です。
おわりに
今回の法則記述は、できるだけインスタンス化しないで、大規模高次な世界を(下部構造に落とさないで)そのまま記述するように試みました。大規模高次なポイントフリースタイルと言っていいかも知れません。
テレオロジー圏を定義する際に最初に与える素材〈構成素〉は次のものです。
- 圏 $`\cat{C}`$
- モノイド圏 $`(\cat{M}, \otimes, I, \alpha, \lambda,\rho)`$
- 右モノイド作用 $`(R = (\ract), \alpha, \rho)`$
- 圏 $`\cat{T}`$
- 関手 $`J:\cat{C}\times\cat{C}^\op \to \cat{T}`$
- 射の族 $`\varepsilon : |\cat{M}|_0 \times|\cat{C}|_0\times|\cat{C}^\op|_0 \to |\cat{T}|_1`$
$`\varepsilon`$ に関する自然性/対角自然性/左ラックス作用性がテレオロジー圏を規定する公理〈等式的法則〉です。公理を提示する準備段階で、色々な圏・関手・自然変換を構成しました。例えば、反ラックス・モノイド関手 $`({^\cap T}, \ul{\alpha}, \ul{\lambda}, \ul{\rho)}`$ は中間的に必要とされる構造でした。
テレオロジー圏のような大規模高次な代数系になると、定義するだけでもけっこうな作業量なので、効率的な定義方法を工夫する必要があります。無法則コンストラクタを先に提示する方法は、けっこう効率的だし、プログラミング言語による実装とも相性が良いだろうと思います。
*1:雰囲気的な例え話で言えば; $`{\bf CAT}`$ が都市部で $`\WCAT`$ は周縁部あるいは郊外も含めた地域です。周縁部は都市部のように洗練されていませんが、多種多様な人々が住んでいます。